一种基于数据驱动的电力系统潮流计算方法与流程

1.本发明属于电力系统分析领域，具体涉及一种基于数据驱动的电力系统潮流计算方法(data
‑
driven power flow method,ddpf)。


背景技术：

2.潮流计算是电力系统中最重要的计算方法之一，在电力系统规划、运行和控制等方面有着广泛应用。最早提出的潮流计算方法包括高斯赛德尔法和牛顿
‑
拉夫逊法，与高斯赛德尔法相比牛顿
‑
拉夫逊法有更好的收敛性和更高的计算效率。为了进一步提高牛顿
‑
拉夫逊法的计算效率，研究人员提出了快速分解法。在新兴的智能电网中，现有的模型驱动计算方法显现出以下几点显著缺点：(1)在智能电网中，出力和负荷的间歇性和不确定性变得愈加明显，这将使得传统牛顿
‑
拉夫逊法和快速分解法难以收敛，这是因为两种算法通常使用前一个数据的潮流计算结果作为初始值；(2)电网参数具有一定的不确定性，存储在电网调控中心数据库中的电网参数可能与实际值存在差异，这使得对模型驱动的计算方法产生负面影响。
3.发明目的
4.本发明的目的即在于应对现有技术中所存在上述不足中的至少之一，少提供一种有用的商业选择，通过提出一种基于数据驱动的潮流计算方法，能够避免复杂的收敛问题，具有较高的计算效率，并且能够处理不同的拓扑结构，能够适应智能电网拓扑结构的频繁变化。


技术实现要素：

5.本发明提供了一种基于数据驱动的电力系统潮流计算方法，包括以下步骤：
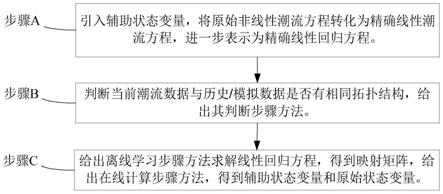
6.步骤a.引入辅助状态变量，将原始非线性潮流方程转化为精确线性潮流方程，进一步表示为准确线性向量矩阵回归方程y＝hz v；
7.步骤b.给出判断当前潮流数据与历史/模拟数据是否有相同拓扑结构的步骤方法，计算判断是否有相同拓扑结构。
8.步骤c.给出离线学习步骤方法求解线性回归方程，得到映射矩阵给出在线计算步骤方法，得到辅助状态变量最后进行线性和非线性变换得到状态变量u
i
、θ
i
。
9.对于步骤a包括：
10.步骤a1：将原始非线性潮流方程转化为精确的线性潮流方程，其中p
i
和q
i
是节点i的有功无功注入功率，k(i)是与节点i直接相连的所有节点(包含i)，原始非线性潮流方程为转化为精确地
线性潮流方程：其中r
ij
＝v
i
v
j
cosθ
ij
，i
ij
＝v
i
v
j
sinθ
ij
和为辅助状态变量。
11.引入辅助状态变量后，将原非线性潮流方程转化为相应的线性方程。对于不同的pq和pv节点，建立相应的线性潮流方程，总个数为2(n
‑
1)，辅助状态变量的总个数为n
‑
1 2b，其中b为支路数。
12.步骤a2：基于步骤a1得到的精确线性潮流方程，进一步表示为其中是辅助边界向量，是辅助状态向量，是一个常数矩阵，其元素由网络的拓扑结构和参数决定。进一步得到准确线性回归方程其中是依赖于网络拓扑和网络参数的未知常数映射矩阵，假设有s个具有相同拓扑结构的历史/模拟潮流数据，并且每个数据包含给定的边界条件和潮流计算结果，将所有这s个历史/仿真潮流数据的辅助边界向量和辅助状态向量聚合，通过离线学习阶段得到h的估计值。是当期望值e(v)＝0时历史/模拟数据中可能存在的误差。
13.优选地，所述步骤b包括处理不同的拓扑结构，判断当前潮流数据与历史/模拟数据是否有相同拓扑结构。
14.优选地，所述步骤b进一步包括以下子步骤：
15.子步骤b1：取任意两个历史数据，基于步骤a计算其相应的辅助边界向量和如果和有很强的的线性相关性，则可以认为它们具有相同的拓扑结构。
16.子步骤b2：判断其线性相关性，若则认为其具有交响的线性相关性，其对应的拓扑结构是相同的。r
threshold
的取值非常重要，但在大量的仿真实验中发现即使r
threshold
取值为0.9，上述方法仍然可以正确识别具有完全相同拓扑结构的历史量测数据。使用rcc代替pearson相关系数(pcc)，是因为rcc不要求辅助量测向量服从正态分布，并且rcc在历史数据中存在显著误差时具有鲁棒性。
17.优选地，所述步骤c中，基于步骤a、b，给出离线学习步骤得到映射矩阵并通过在线计算阶段得到辅助状态变量，最后进行非线性和线性变换得到状态变量。
18.优选地，所述步骤c进一步包括以下子步骤：
19.子步骤c1：基于步骤a，将拓扑结构相同的历史/模拟潮流数据聚合起来，忽略共线性影响，使用加权最小二乘(wls)方法直接估计映射矩阵h。可以得到估计的映射矩阵历史/模拟潮流数据个数s与辅助状态变量个数2(n
‑
1)的比例影响着映射矩阵的精度，保证s≥2(n
‑
1)时可用；
20.子步骤c2：基于步骤b，快速找到与当前潮流数据拓扑结构相同的历史/模拟数据，
得到相应的矩阵，通过得到当前数据的辅助状态向量。其中和是当前潮流数据的辅助边界向量和估计的辅助状态向量；
21.步骤c3：潮流计算的解是辅助状态变量，通过非线性和线性变换得到原始状态变量。
22.更优选地，所述子步骤b1进一步包括：
23.步骤b11：计算
24.更优选地，所述子步骤c1进一步包括：
25.步骤c11：计算
26.更优选地，所述步骤c2进一步包括：
27.步骤c21：计算
附图说明
28.图1为本发明所述基于数据驱动的潮流计算方法的流程图。
29.图2为本发明具体实施例中所选取ieee300节点系统中6组辅助边界向量的rcc相关矩阵。
30.图3为本发明具体实施例中不同ieee系统的ratio与|dv|
m
关系。
31.图4为本发明具体实施例中不同ieee系统的ratio与|dθ|
m
关系。
具体实施方式
32.本发明一种基于数据驱动的潮流计算方法(data
‑
driven power flow method,ddpf)，基于数据驱动的潮流计算方法没有收敛问题，在保证相似计算精度的情况下，计算效率远远高于传统牛顿
‑
拉夫逊法和快速分解法。仿真算例验证了所提方法无收敛性问题和很高的计算效率，适合于大规模网络的在线应用。
33.本发明的附加优点将在下面的描述中部分给出，通过下面的描述变得更加明显。
34.下面结合附图，对本发明进一步详细说明。
35.如图1所示，本发明所述基于数据驱动的潮流计算方法，包括以下步骤：
36.步骤a.引入辅助状态变量，将原始非线性潮流方程转化为精确线性潮流方程，进一步表示为准确线性向量矩阵回归方程y＝hz v，提出基于数据驱动的潮流求解方法，建立线性求解方程，使其无计算收敛性问题。步骤a进一步包括以下子步骤：
37.步骤a1：引入辅助状态变量r
ij
、i
ij
、u
i
，将原始非线性潮流方程转化为精确的线性潮流方程，原始非线性潮流方程为：
38.p
i
＝v
i
∑
j∈k(i)
v
j
(g
ij
cosθ
ij
b
ij
sinθ
ij
)
ꢀꢀ
(1)
39.q
i
＝v
i
∑
j∈k(i)
v
j
(g
ij
sinθ
ij
‑
b
ij
cosθ
ij
)
ꢀꢀ
(2)
40.式中：p
i
和q
i
是节点i的有功无功注入功率，k(i)是与节点i直接相连的所有节点(包含i)，g
ij
jb
ij
是节点导纳矩阵元件，在保证一般性的情况下，假定节点i为松弛节点，电压幅值相角为v
i
∠θ
i
(i＝2,3,
…
,n)。转化为精确地线性潮流方程：
41.p
i
＝g
ii
u
i
∑
j∈k(i),j≠i
(g
ij
r
ij
b
ij
i
ij
)
ꢀꢀ
(3)
42.q
i
＝
‑
b
ii
u
i
∑
j∈k(i),j≠i
(g
ij
i
ij
‑
b
ij
r
ij
)
ꢀꢀ
(4)
43.式中：r
ij
＝v
i
v
j
cosθ
ij
，i
ij
＝v
i
v
j
sinθ
ij
和为辅助状态变量。
44.对于每一个pv节点，建立方程：
45.u
i.pv
＝u
i
ꢀꢀ
(5)
46.式中：并且v
i.pv
是给定的第i个pv节点电压幅值。
47.引入辅助状态变量后，将原非线性潮流方程转化为相应的线性方程。对于不同的pq和pv节点，建立相应的线性潮流方程，总个数为2(n
‑
1)，辅助状态变量的总个数为n
‑
1 2b，其中b为支路数。
48.步骤a2：提出基于数据驱动的潮流求解方法，建立精确线性回归方程，形成待求解映射常数矩阵h。
49.基于步骤a1得到的精确线性潮流方程，进一步表示为：
[0050][0051]
式中：是辅助边界向量，是辅助状态向量，是一个常数矩阵，其元素由网络的拓扑结构和参数决定。根据式(4)得到精确线性回归方程：
[0052][0053]
式中：是依赖于网络拓扑和网络参数的未知常数映射矩阵，通过离线学习阶段得到。是当期望值e(v)＝0时历史/模拟数据中可能存在的误差。
[0054]
使用大量的历史/模拟潮流数据来学习得到h，假设有s个具有相同拓扑结构的历史/模拟潮流数据，并且每个数据包含给定的边界条件和潮流计算结果。将所有这s个历史/仿真潮流数据的辅助边界向量和辅助状态向量聚合为：
[0055][0056][0057]
式中：和分别是第i个历史/模拟潮流数据中的辅助边界向量和辅助状态向量。y和z可由准确线性回归方程y＝hz v得到，其中是当期望值e(v)＝0时的误差矩阵。
[0058]
步骤b.处理不同的拓扑结构，判断当前潮流数据与历史/模拟数据是否有相同拓扑结构。
[0059]
步骤b1：取任意两个历史数据，基于步骤a计算其相应的辅助边界向量和如果和有很强的的线性相关性，则可以认为它们具有相同的拓扑结构。统计学中斯皮尔曼等级相关系数(rcc)可以用来衡量之间的相关性：
[0060]
[0061]
式中：是两个辅助边界向量的等级差，rg(*)代表从小(从1开始)到大的连续排序数，和是和的第i个元素，m代表辅助边界向量元素个数
[0062]
步骤b2：判断其线性相关性，若则认为其具有交响的线性相关性，其对应的拓扑结构是相同的。r
threshold
的取值非常重要，但在大量的仿真实验中发现即使r
threshold
取值为0.9，上述方法仍然可以正确识别具有完全相同拓扑结构的历史量测数据。使用rcc代替pearson相关系数(pcc)，是因为rcc不要求辅助量测向量服从正态分布，并且rcc在历史数据中存在显著误差时具有鲁棒性。
[0063]
步骤c.给出离线学习步骤方法求解线性回归方程，得到映射矩阵给出在线计算步骤方法，得到辅助状态变量最后进行非线性和线性变换得到状态变量u
i
、θ
i
。
[0064]
步骤c1：基于步骤a，将拓扑结构相同的历史/模拟潮流数据聚合起来，忽略共线性影响，使用加权最小二乘(wls)方法直接估计映射矩阵h。
[0065][0066]
可以得到估计的映射矩阵历史/模拟潮流数据个数s与辅助状态变量个数2(n
‑
1)的比例影响着映射矩阵的精度，保证s≥2(n
‑
1)时可用。
[0067]
步骤c2：基于步骤b，快速找到与当前潮流数据拓扑结构相同的历史/模拟数据，得到相应的矩阵，通过得到当前数据的辅助状态向量。其中和是当前潮流数据的辅助边界向量和估计的辅助状态向量。
[0068]
步骤c3：潮流计算的解是辅助状态变量，将辅助状态变量变换为中间变量y
i
并定义为
[0069]
y
i
＝[u
i,i
；θ
ij,i
]
ꢀꢀ
(12)
[0070]
中间状态变量与所求的辅助状态变量之间存在如下的非线性变换关系：
[0071][0072]
最后状态变量可由式(14)得到：
[0073][0074]
式中，a
e
为电力系统中降阶的节
‑
支关联矩阵(不包含松弛节点)。在线计算阶段的主要计算来自于矩阵乘法，这比传统的牛顿
‑
拉夫逊法和快速分解法更加简便。
[0075]
所述步骤b1包括：
[0076]
步骤b11：计算
[0077]
所述步骤c1包括：
[0078]
步骤c11：计算
[0079]
所述步骤c2包括：
[0080]
步骤c21：计算
[0081]
为使本领域技术人员更好地理解本发明以及了解本发明相对现有技术的优点，下面结合具体实施例进行进一步的阐释。
[0082]
如图2所示，首先选取ieee300节点系统中6组辅助边界向量来验证rcc的准确性，其次令ratio＝s/(2(n
‑
1))测试离线学习阶段使用的数据量对所提ddpf方法精度的影响，与现有两种ddpf算法进行比较，检验所提方法的计算精度。最后采用ieee14、30、33、57、118、123、300节点系统，在出力、负荷不确定、拓扑结构频繁变化两种情况下，与传统nrpf和fdpf算法进行了性能测试和比较，nrpf和fdpf的计算采用matpower(收敛精度为10
‑8)，来说明本文算法在大规模网络潮流计算中的适用性。
[0083]
1、准确性分析
[0084]
为了验证基于rcc的拓扑识别方法准确性，从ieee
‑
300节点系统中选取6组辅助边界向量，分别对应三组不同的拓扑结构，即和和和和和每组具有相同的拓扑结构。计算rcc相关矩阵：
[0085][0086]
式中：是两个辅助边界向量的等级差，rg(*)代表从小(从1开始)到大的连续排序数，和是和的第i个元素。
[0087]
如图2所示，rcc方法可以准确识别相同的拓扑结构，另外在其它ieee系统的拓扑识别结果都是正确的。
[0088]
2、精确性分析
[0089]
本发明所提出的算法是对数据驱动潮流算法的改进。为说明算法的准确性，分别对另外两种数据驱动算法ddpf
(1)
和ddpf
(2)
与本发明提出的算法进行仿真分析。
[0090]
图3
‑
4给出了不同比值ratio＝s/(2(n
‑
1))(0.1
‑
1.2)下，真实值与本文所提ddpf方法之间的误差，包含电压幅值的平均绝对误差|dv|
m
和相角的平均绝对误差|dθ|
m
。结果表明，随着比值的增加，|dv|
m
和|dθ|
m
均随之减小，另外从表1可以看出，本文所提ddpf方法得到的|dv|
m
与|dθ|
m
均小于ddpf
(1)
和ddpf
(2)
中给出的结果。
[0091]
表1 ratio＝1时不同ddpf方法得到的|dv|
m
与|dθ|
m
[0092][0093]
由此可以证明本文所提ddpf方法具有较高的计算精度，并且当ratio＝0.2时，|dv|
m
和|dθ|
m
均小于10
‑4，这表示本文方法在历史/模拟数据相较少的情况下依然可以使用。
[0094]
3、收敛性及计算效率分析
[0095]
假设出力和负荷的不确定性使得电压幅值在0.95
‑
1.05之间随机变化，相角在
‑
15
°‑
15
°
之间随机变化，使用前一个数据的状态变量作为传统牛顿
‑
拉夫逊法和快速分解法的初始值。表2给出了不同方法在100次测试中不收敛的次数η。
[0096]
表2 100次测试中不同潮流算法在不确定性下的计算结果
[0097][0098]
由表2的数据可知，当出力和负荷出现不确定性，nrpf和fdpf算法在大部分测试中很难收敛，而本文所提的ddpf算法在所有情况下都能获得相当准确的结果，由于ddpf算法的在线计算阶段不需要迭代计算，所以迭代次数为0，在所列出的潮流算法中，本文所提的ddpf方法的在线计算效率远远高于其他方法，更适合于大规模网络。
[0099]
4、适应性分析
[0100]
在100个连续潮流样数据中，假设拓扑结构连续变化，对于每个采样数据，分别测试nrpf、fdpf和本文ddpf算法。在所有测试中，均使用前一个数据的状态变量作为传统牛顿
‑
拉夫逊法和快速分解法的初始值。表3给出了nrpf和fdpf在测试中不收敛次数η。
[0101][0102]
从表3可以看出，当拓扑结构频繁变化时，传统nrpf和fdpf算法难以收敛，而在所有测试中，本文所提ddpf算法依然能够找到与当前数据拓扑结构线条的历史/模拟数据，并且得到与表1相同精度的潮流解。表3页给出了平均迭代次数和计算时间，表明即使在拓扑结构频繁变化的情况下也能获得较高精度的潮流解，并且保证一定的计算效率。
[0103]
通过以上的仿真分析可以看出，本发明的计算方法在大规模网络潮流计算中具有优势，具体表现在：不存在收敛问题，计算效率高，并且能够处理不同的拓扑结构，能够适应智能电网拓扑结构的频繁变化。
[0104]
上述实施例对本发明的技术方案进行了详细说明。显然，本发明并不局限于所描
述的实施例。基于本发明中的实施例，熟悉本技术领域的人员还可据此做出多种变化，但任何与本发明等同或相类似的变化都属于本发明保护的范围。