基于超颖表面的结构光场坐标变换与复合全息方法

本发明涉及一种结构光场变换方法，尤其涉及一种基于介质超颖表面的结构光场坐标变换与复合全息应用方法，属于微纳光学、结构光束领域。

背景技术：

1、随着科学技术的不断发展以及工业需求的日益增长，传统的平面光束和高斯光束已不再满足现代光学设计的要求。结构光束，作为一种新兴的光场形态，正在逐渐广泛应用于各种光学研究和工业制造领域。结构光束凭借其根植于麦克斯韦方程组的自由光场解，能够实现高度复杂的光场形态变换。然而，随着应用需求的扩大，结构光束正经历着从简单模态向复杂模态的过渡阶段。简单模态的结构光束，类似于高斯光束，逐渐无法满足实验需求，而复合模态的结构光束则引入了过于丰富的空间变化，难以与实际应用需求相匹配。面对这一挑战，结构光束领域正迫切需要突破，以实现更自由的光场形态设计。

2、除了结构光束，全息光学也是现代光学应用领域的另一个重要分支。全息光学提供了绝对自由的光场形态设计，依赖算法优化和计算机辅助设计，能够实现任意复杂的光场形态。然而，全息光场通常伴随着离焦和弥散特性，无法像结构光束那样在三维空间中构建理想的空间轨迹，从而严重限制了光场调控的设计自由度。因此，如何将结构光束的空间传输轨迹灵活性与全息光学的自由形态图案优化相结合，成为一个备受关注和发展的方向。厄米特高斯光束和拉盖尔高斯光束是两种最基本的单模结构光束，su2光束、lissajous光束等复杂结构光场的衍生变化能够由这两种光束演变叠加而成。

3、超表面，作为近年来逐渐崭露头角的光学应用平台，在光学设计、全息应用和结构光束领域都具有巨大潜力。超表面凭借微纳米级别的结构尺度、自由度极高的像素设计和多重光学性质的可调性，在光学研发和工业应用中扮演着重要角色。因此，如果尝试实现结构光束与全息光场的综合应用，超表面将是一个极具潜力的选择。

技术实现思路

1、为解决现有技术中结构光束设计灵活性受限、与全息光场配合调制困难等问题。本发明的主要目的是提供一种基于超颖表面的结构光场坐标变换与复合全息方法，将基于alias变换方法的坐标系变形方式引入结构光场的构建中，实现结构光束形态的自由变化；利用超颖表面空间复用设计方法，配合全息图像信息构建复合光场，不仅能够实现结构光束任意变形与和光学全息复合，而且能够进一步提高光场信息综合应用的能力。

2、本发明的目的是通过下述技术方案实现的：

3、本发明公开的基于超颖表面的结构光场坐标变换与复合全息方法，为了实现结构光束与光学全息复合应用的光场构建，首先针对基本结构光束厄米特高斯光束(hermite-gaussian，hg)与拉盖尔高斯光束(laguerre-gaussian，lg)进行坐标变形。变形采用alias坐标变换方法，对基本的笛卡尔坐标系和极坐标系进行坐标系变形。坐标系对应的结构光束信息分布特征同样发生变形。依据复合模式结构光场构建方法，在坐标变换条件下，能够构建自由形式的复合模式结构光束。应用几何相位超颖表面实现变形结构光束的信息表达。利用组合天线的方法，通过几何相位纳米天线的组合实现超像素的复振幅控制。针对超颖表面进行结构光束表达未利用到的信息空间，利用掩膜全息优化方法，实现光学全息的综合表达。变形结构光束和光学全息信息在光场实空间和傅立叶面空间分别呈现，进一步提高光场信息量和综合应用的能力。

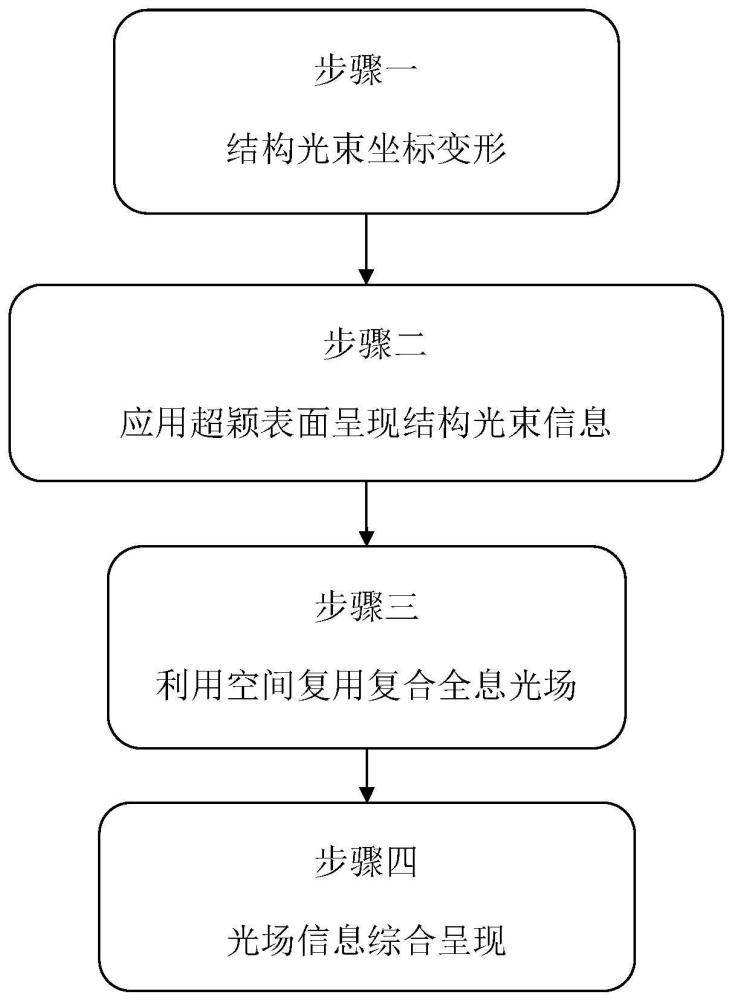
4、本发明公开的基于超颖表面的结构光场坐标变换与复合全息方法，包括如下步骤：

5、步骤一：针对基本结构光束厄米特高斯光束hg(hermite-gaussian)与拉盖尔高斯光束lg(laguerre-gaussian)进行坐标变形。变形采用alias坐标变换方法，对基本的笛卡尔坐标系和极坐标系进行坐标系变形。坐标系对应的结构光束信息分布特征同样发生变形。依据复合模式结构光场构建方法，在坐标变换条件下，能够构建自由形式的复合模式结构光束。

6、作为最基本的单模结构光束，厄米特高斯光束和拉盖尔高斯光束是波动方程在笛卡尔坐标系和极坐标系下的本征解，因此，厄米特高斯光束和拉盖尔高斯光束之间存在紧密的转换关系。

7、厄米特高斯模式函数：

8、

9、拉盖尔高斯模式函数:

10、

11、公式(1)和公式(2)分别代表厄米特高斯光束和拉盖尔高斯光束的基本光束模式特征。其中，hgm,n表示厄米特高斯模式光场复振幅信息；lgp,l表示拉盖尔高斯模式光场复振幅信息；x，y表示笛卡尔坐标系；r，θ表示极坐标系；m,n分别代表x和y方向的阶数；p代表径向系数，l代表拓扑荷数；和表示光场的强度信息；hm和hn表示x和y方向的厄米特函数，表示极坐标系的拉盖尔函数；w0表示束腰半径，z表示传播距离，zr表示瑞利范围；θg＝arctan(z/zr)表示古依相移。

12、厄米特高斯光束和拉盖尔高斯光束之间的转换关系：

13、

14、

15、公式(3)表示厄米特高斯光束和拉盖尔高斯光束之间的转换关系；公式(4)表示wigner d参数；其中(m,n)和(l,p)参数之间的转化关系由p＝min(m,n)和l＝m-n表示；n＝m+n表示结构光束的模式阶数；k，v表示计算的过程参数。

16、厄米特高斯光束和拉盖尔高斯光束作为两种基本模式光束，在形式转换上具有变换自由，但是光束变化的所有自由度都局限在基本参数的设计自由之中，不能够实现任意自由变形。因此需要通过基本坐标定义方式的改变来引入变换的新灵活性。

17、alias坐标变换方法利用不同坐标系间的位置转换关系构建坐标系变形，因此将alias坐标变换方法引入结构光束构建过程能够实现厄米特高斯光束和拉盖尔高斯光束的灵活变化。在传统笛卡尔坐标系(x,y)和极坐标系(r,θ)条件下，通过引入alias坐标变换方法，建立新坐标系(u,v)和用于实现变形结构光束的重新表达。通过雅可比矩阵构建四个坐标系之间的关系。针对变形拉盖尔高斯光束，新旧坐标系统(r,θ)和之间的关系用表达，其中θ表示极坐标方位角，r表示极坐标半径，f(θ)表示以方位角为变量任意形式闭合函数，表示新坐标系统角向坐标参数，表示的微分，ρ表示新坐标系统径向坐标参数。定义连接(u,v)到的雅可比矩阵为j1，连接到(r,θ)的雅可比矩阵为j2，连接(x,y)到(r,θ)的雅可比矩阵是j3，连接(u,v)到(x,y)的雅可比矩阵是j。因此电磁场坐标转换的雅可比矩阵表示为：

18、

19、表示坐标变换前电磁场属性，表示坐标变换后电磁场属性，其中j＝j1×j2×j3-1。针对不同坐标系之间的变换关系，四种基础的坐标系表达方式(x,y),(r,θ),(u,v)和被用来构建变形厄米特高斯和拉盖尔高斯模式hlg(hermite-laguerre-gaussian)与传统hlg模式之间的关联。针对传统坐标和新建坐标，极坐标与轴向坐标的转换关系表示为：

20、

21、

22、变换坐标和传统坐标之间的转换关系表示为:

23、

24、对于极坐标而言，变换关系如下:

25、

26、由雅克比矩阵表达上述转换关系如下:

27、

28、

29、

30、

31、因此，得到从坐标系(u,v)到坐标系(x,y)的雅可比行列式。

32、

33、经坐标系变换后的物理场空间可以通过雅可比矩阵表示为:

34、

35、

36、在此基础上，新电磁场(u,v)中光束属性表示为：

37、

38、旧电磁场(r,θ)中,光束表示为：

39、

40、从公式(17)和公式(18)中，能够通过r＝f′(θ)定义变形电磁场中的光束性质，实现将光束变形成任意给定的形状。

41、根据以上alias变换规则，将hlg模光束对应变换成任意需要的光束形态，在笛卡尔坐标系(x,y)条件下,变换的hlg光束表示为:

42、

43、其中α表示方位角，β表示极向角。

44、步骤二：应用几何相位超颖表面实现变形结构光束的信息表达。利用组合天线的方法，通过几何相位纳米天线的组合实现超像素的复振幅控制。

45、几何相位超颖表面通过控制纳米柱天线的旋转角度在正交圆偏通道下实现纯相位调制，针对单个纳米柱天线，天线旋转角度由θ表示，σ＝-1表示反向圆偏输出光场的特征，调制相位表示为针对结构光束复振幅调制需求，采用2×2超像素结构，利用几何相位纳米柱天线实现复振幅控制。复振幅信息表示为：

46、

47、

48、其中超像素结构主对角线两个天线结构具有相同旋转角度θ1，副对角线两个天线结构具有相同旋转角度θ2。a表示调制后振幅信息，表示调制后相位信息。两个旋转角度对应计算表示为：

49、步骤三：针对超颖表面进行结构光束表达未利用到的信息空间，利用掩膜全息优化方法，实现光学全息的综合表达。

50、将变形结构光束的复振幅光场信息用几何相位超颖表面进行表达，会存在一定空间的信息空余。将空余信息空间位置作为掩膜，能够实现光学全息的表达，实现光场信息的充分利用。全息优化采用gerchberg-saxton(gs)优化方法，在傅立叶面观察到设计对应的图案特征。全息信息采用纯相位调制方法实现，即超颖表面单个天线构成独立的像素控制。

51、步骤四：变形结构光束和光学全息信息在光场实空间和傅立叶面空间分别呈现，即实现基于超颖表面的复合全息，进一步提高光场信息量和综合应用的能力。

52、复合光场观察方法如下：

53、使用超连续激光器用于提供800nm的激光光束。入射光源通过偏振调制器件偏振片lp1、lp2矫正入射光源的线偏特征，利用四分之一波片qwp1将线性偏振光转化为左旋圆偏光。光束准直照射到超颖表面后经过显微物镜object与透镜f1构成的显微镜系统放大。通过qwp2和lp3用以检测相反旋向的圆偏输出。观察频谱面全息图案特征时，将照相机放置在频谱面位置，即透镜f1的后焦面位置时，能够观察到理想全息图案与结构光束的傅立叶变换效果。观察实空间变形结构光束特征时，将光阑ap放置在透镜f1的后焦面位置遮挡全息图案信息。再放置傅立叶透镜f2，能够在f2后焦面位置观察到重构的变形结构光束图案，即实现基于超颖表面的复合全息，进一步提高光场信息量和综合应用的能力。

54、有益效果：

55、1、本发明公开的基于超颖表面的结构光场坐标变换与复合全息方法，坐标变形采用alias坐标变换方法，对基本的笛卡尔坐标系和极坐标系进行坐标系变形。坐标系对应的结构光束信息分布特征同样发生变形。依据复合模式结构光场构建方法，在坐标变换条件下，能够构建自由形式的复合模式结构光束。应用几何相位超颖表面实现变形结构光束的信息表达。利用组合天线的方法，通过几何相位纳米天线的组合实现超像素的复振幅控制。针对超颖表面进行结构光束表达未利用到的信息空间，利用掩膜全息优化方法，实现光学全息的综合表达。变形结构光束和光学全息信息在光场实空间和傅立叶面空间分别呈现，进一步提高光场信息量和综合应用的能力。

56、2、本发明公开一种基于超颖表面的结构光场坐标变换与复合全息方法，将基于alias变换方法的坐标系变形方式引入结构光场的构建中，实现结构光束形态的自由变化。

57、3、本发明公开一种基于超颖表面的结构光场坐标变换与复合全息方法，应用超颖表面实现结构光场和光学全息空间复用的综合设计，实现多类型复合光场综合应用。

58、4、本发明公开一种基于超颖表面的结构光场坐标变换与复合全息方法，变形结构光束和光学全息信息在光场实空间和傅立叶面空间分别呈现，通过在实空间和频谱空间分别观察变形结构光束和光学全息，实现多空间光学信息的复合应用。