一种高速分布式电动汽车稳定性控制方法

本发明涉及一种高速汽车主动安全控制，特别是一种高速分布式电动汽车稳定性控制方法。

背景技术：

1、稳定性控制是分布式电动汽车的关键技术之一，其核心目标是通过合理的控制各个轮毂电机、方向盘转角，减少车辆失稳情况的发生，同时当车辆发生失稳时及时纠正，使其具备良好的行驶稳定性和安全性。在高速驾驶环境中，所述高速指代车辆速度在72km/h以上的速度工况，汽车轮胎受力极易进入非线性工作区域，轮胎纵向力和侧向力之间存在耦合和制约关系。如果车轮的驱动力矩过大，则能产生的侧向力便很小，可能导致侧滑；如果车辆在极限工况下驾驶员因操作不当，转动一个不合理的方向盘转角值，车辆所需的侧向力增大，那么将加速车辆失稳。然而现有分布式电动汽车稳定性控制方法在综合考虑横纵向控制方面有所欠缺。因此，如何综合考虑横、纵向运动控制，使分布式电动汽车具备良好的稳定性和安全性的问题亟待解决。

技术实现思路

1、为解决现有技术存在的上述问题，本发明的目的在于提供一种高速分布式电动汽车稳定性控制方法，能够有效提升汽车稳定性和安全性。

2、为了实现上述目的，本发明的技术方案如下：

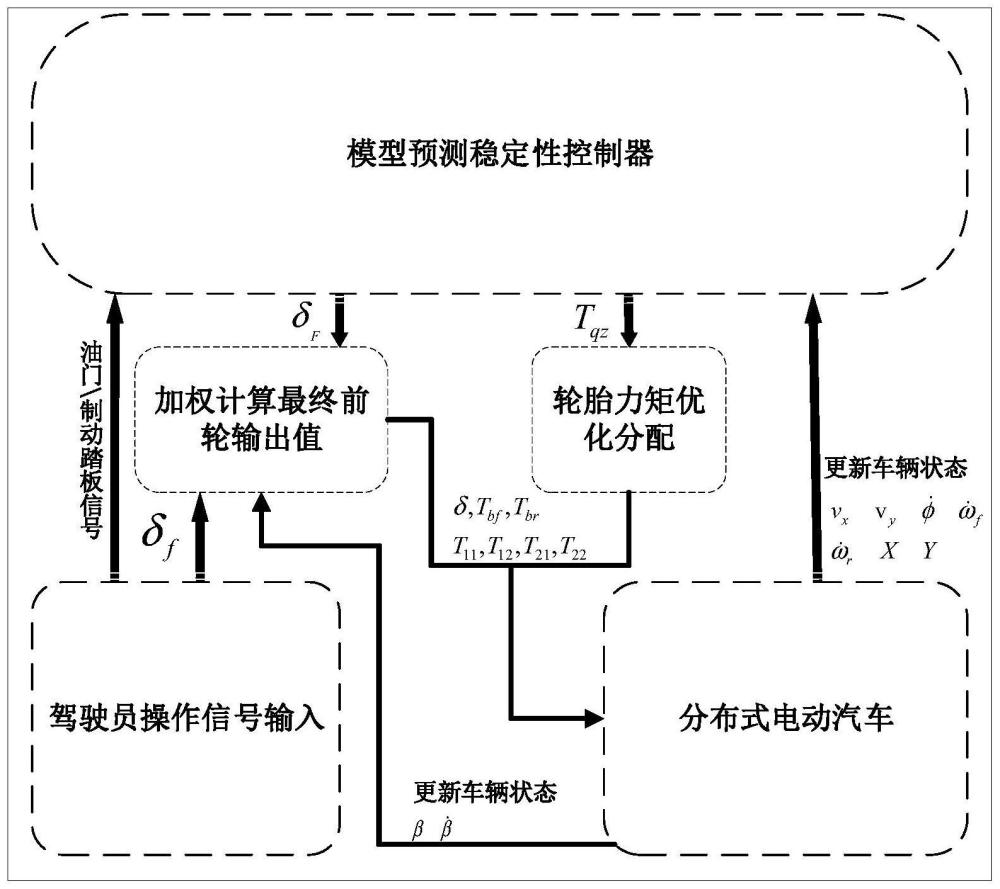
3、一种高速分布式电动汽车稳定性控制方法，利用高速分布式电动汽车稳定性控制系统进行控制，所述高速分布式电动汽车稳定性控制系统包括初始化模块、驾驶员操作信号输入模块、模型预测稳定性控制器、车轮力矩优化分配模块、加权计算最终前轮输出值模块。

4、所述初始化模块负责检查车辆通信链路是否正常工作、底盘相关模块信号收发是否正常，加载车辆动力学参数。

5、所述驾驶员操作信号输入模块采集油门/制动踏板信号和方向盘角度信号，将油门踏板/制动踏板信号换算为驾驶员期望的总驱/制动力矩，将方向盘角度信号换算为驾驶员期望的前轮转动的角度。

6、所述模型预测稳定性控制器负责根据车辆状态信息及驾驶员操作信息计算出整车总驱/制动力矩和稳定性前轮转角补偿值。所述整车总驱/制力矩是根据车辆状态信息及驾驶员操作信息计算出相应的整车驱动力矩或制动力矩。所述的稳定性前轮转角补偿值是基于车辆稳定性应对高速失稳及临界失稳情况下补偿驾驶员因操作不当而输出的前轮转角值。

7、所述车轮力矩优化分配模块负责接收模型预测稳定性控制器计算出的整车总驱/制动力矩，对整车驱/制动力矩优化分配，计算出四个轮毂电机驱动力矩矩或前后车轮制动力矩。

8、所述加权计算最终前轮输出值模块负责接收采集到的驾驶员期望前轮转角δf和模型预测稳定性控制器计算出的稳定性前轮转角补偿值，并根据车辆稳定性状况，加权计算出最终的前轮转角控制量δ。

9、所述控制方法包括以下步骤：

10、步骤1：初始化模块进行检查和加载

11、检查车辆通信链路是否正常工作、底盘相关模块信号收发是否正常，加载三自由度车辆动力学模型参数。

12、以数学方程的形式建立所述三自由度车辆动力学模型如下：

13、

14、其中：m为车辆质量；vy为侧向车速；vx为纵向车速；为横摆角速度；为横摆角加速度；iz为转动惯量；lf和lr分别为前后车轴到质心处的距离；cαf和cαr分别为前后轮的侧偏刚度；iw为轮胎转动惯量；rw为轮胎滚动半径；汽车前轮角加速度；汽车后轮角加速度；δf为前轮转角补偿值，区别于驾驶员因转动方向盘输入的前轮转角值δf；tm为总驱动力矩；tbf为前轮制动力矩；tbr为后轮制动力矩；tm、tbf、tbr三者的关系如下：

15、tqz＝tm-tb

16、tb＝tbf+tbr

17、式中：tqz为总驱/制动力矩，tb为总制动力矩。

18、步骤2：获取驾驶员的操作输入信息

19、驾驶员操作信号输入模块采集油门踏板/制动踏板信号和方向盘角度信

20、号，并根据如下计算公式：

21、

22、

23、将油门踏板/制动踏板信号换算为驾驶员期望的总驱/制动力矩tqzd，将方向盘角度信号换算为驾驶员期望的前轮转动的角度δf。

24、式中：ad为驾驶员期望的车辆加/减速度；kj为油门踏板开度与期望的加速度之间的比例系数；kz为制动踏板开度与期望的减速度之间的比例系数；pj为油门踏板开度；pz为制动踏板开度；δsw为方向盘转动角度；is为汽车转向系统传动比。

25、步骤3：模型预测稳定性控制器计算总驱/制力矩和前轮转角补偿值

26、模型预测稳定性控制器将驾驶员操作信号、车辆状态信息、上一时刻前轮转角补偿值及上一时刻总驱/制动力矩输入模型预测稳定性控制器，所述车辆状态信息为车辆当前纵向速度、当前横向速度、当前横摆角速度、当前前轮角加速度、当前后轮角加速度，当前纵向位置信息x、当前横向位置信息y。对三自由度车辆动力学模型进行微分平坦化，得到平坦化系统，利用平坦化系统设计线性时变模型预测控制器，所述的平坦化系统状态空间方程如下：

27、

28、式中：f(t)为平坦化系统的状态量矩阵，它的表达式为其中的p1,p2,为系统的状态量；v(t)为平坦化系统控制输入矩阵，它的表达式为[v1,v2]t，其中的v1,v2为平坦化系统的两个控制量；yf(t)为平坦化系统的输出矩阵，它的表达式为其中yf1,yf2,为平坦化系统的输出量；af为平坦化系统状态方程中状态量矩阵的系数矩阵，它的表达式为：

29、

30、bf为平坦化系统状态方程中控制量矩阵的系数矩阵，它的表达式为：

31、

32、cf为平坦化系统输出方程中状态量矩阵的系数矩阵，它的表达式为：

33、

34、所述线性时变模型预测控制器为模型预测稳定性控制器组成部分，主要以线性时变模型预测控制方法计算所述平坦化系统的控制量，之后根据线性时变模型预测控制器计算出的控制量计算出模型预测稳定性控制器的控制量，即总驱/制力矩和前轮转角补偿值。更进一步以数学表达式的形式说明如下：

35、a、根据平坦化系统状态空间方程构建如下预测时域内线性时变模型预测控制器离散化的状态空间方程为：

36、

37、y(k)＝ψξ(k)+θδv

38、式中：ξ(k)为线性时变模型预测控制器状态空间方程的状态量；δv为线性时变模型预测控制器状态空间方程的控制量的增量；f(k)为线性时变模型预测控制器状态空间方程状态量矩阵；y(k)为为线性时变模型预测控制器状态空间方程输出量矩阵；为线性时变模型预测控制器状态空间方程中状态方程的状态量系数矩阵；为线性时变模型预测控制器状态空间方程中状态方程的控制量系数矩阵；ψ为线性时变模型预测控制器状态空间方程中输出方程状态量的系数矩阵；θ为线性时变模型预测控制器状态空间方程中输出方程控制量的系数矩阵；

39、b、设计线性时变模型预测控制器目标函数如下：

40、j＝[y(k)t-y_ref(k)t]q[y(k)-y_ref(k)]+δvtrδv+ρε

41、式中：q和r分别为输出状态量和输入状态量增量的权重矩阵；y_ref(k)为预测时域内参考状态量矩阵；ε为松弛因子；ρ为松弛因子权重。进一步将线性时变模型预测控制器最优控制求解问题转化为含多约束的标准二次规划问题。

42、c、求解标准二次规划，计算出下一时刻平坦化系统控制量

43、将线性时变模型预测控制器计算出的下一时刻控制量换算为模型预测稳定性控制器控制量tqz和δf，控制律转化关系如下：

44、

45、式中：u为模型预测稳定性控制器控制量矩阵，它的表达式为[tqz,δf]t，tqz为模型预测控制器稳定性控制器总驱/制动力矩，δf模型预测控制器稳定性控制器前轮转角补偿值；v为上述平坦化系统控制量矩阵，它的表达式为[v1,v2]t，v1和v2分别为平坦化系统的两个控制量；和是平坦化系统计算过程中的转化矩阵，它们的表达式如下：

46、

47、

48、

49、

50、

51、

52、

53、

54、

55、

56、步骤4：计算驾驶员前轮转角输入值和模型预测稳定性控制前轮转角权重。

57、将步骤2与步骤3所计算出的下一时刻的前轮转角控制量δf、前轮转角补偿值δf及车辆状态信息基于下述规则进行加权，并根据车辆稳定性状况，最终得到前轮转角控制输出量δ下发至底盘。

58、δ＝τ·δf+(1-τ)δf

59、

60、式中：β为质心侧偏角；为质心侧偏角变化率；κ1为相平面边界线的斜率；κm为所述相平面的稳定边界截距；κn为所述相平面非稳定边界的截距。

61、步骤5：进行轮胎力矩优化分配

62、将步骤3所输出的总驱/制动力矩tqz作为轮胎力矩优化分配模块的输入。当tqz＞0时，tqz＝tm，tb＝0，对于tm进行优化分配，构建标准二次规划目标函数，计算出分配给四个轮毂电机的力矩，分别为t11,t12,t21,t22；当tqz≤0

63、时，-tqz＝tb，tm＝0，对于tb进行分配，根据理想制动力分配曲线将tb优化分配为tbf和tbr。最后将所计算的t11,t12,t21,t22或tbf、tbr下发至相关控制器，所述相关控制器为四个轮毂电机控制器，前后轮制动控制器。

64、步骤6：辅助驾驶员进行车辆控制

65、对由步骤4和5计算出的控制量施加控制量约束，并作为控制信号以固定频率下发给分布式电动汽车汽车底盘。并进一步地，判断汽车是否熄火停车，若是，则车辆完成控制任务，否则转步骤1。

66、与现有技术相比，本发明具有以下有益效果：

67、1、本发明基于三自由度车辆动力学模型构建的一种平坦化系统，设计了模型预测稳定性控制器，以提升高速分布式电动汽车安全性和稳定性为目标，基于微分平坦理论和模型预测控制理论同时对纵横向控制进行综合考虑，使得控制品质提升，保证了轮胎力的合理使用，提升了上述车辆的稳定性和安全性。

68、2、根据平坦系统特性，经过平坦化后的系统降低了模型预测稳定性控制器优化求解空间的维数，给模型预测稳定性控制器带来了计算效率的大幅度提升。