一种面向非结构化场景的自动驾驶拖拉机路径规划方法

本发明属于自动驾驶车辆路径规划领域，具体涉及一种面向非结构化场景的自动驾驶拖拉机路径规划方法。

背景技术：

1、传统拖拉机采用人工驾驶完成播种、施肥、果实运输等各种作业任务。但是，实际作业场景中各类障碍物无法避免，传统的作业方式在避障过程中易出现漏行、叠行等现象，存在生产效率低下以及浪费土地资源等问题。近年来，随着我国农业机械逐步向智能化转型，发展精准农业已提上日程。实施精准农业的重要前提是进行路径规划，以引导自动驾驶拖拉机等农业机械根据规划的作业路径行走，即考虑障碍物的位置和布局以确定最优的路径。

2、自动驾驶拖拉机主要行驶在非结构化场景中。由于缺乏清晰的道路标志线且路面条件复杂多样、道路和非道路区域难以区分，传统的依赖车道线或清晰的道路边界进行感知与定位的路径规划方法并不适用。此外，非结构化场景中，若利用摄像头以及激光雷达等传感器数据进行障碍物检测和环境感知以确定安全的行驶路径，不仅实现较为困难且会显著增加系统成本。目前，基于图搜索的方法(如a*算法)可以将状态空间离散成图，并利用离线地图建模的方式获得非结构化场景下的参考路径，避免过分依赖传感器数据。但是，此类方案对拖拉机的运动学约束考虑不够全面(路径曲率可能存在突变)，无法处理场景中存在动态障碍物或动态障碍物运动方向不固定的情况。另一方面，借助数值优化方法(如动态规划算法)，也可以实现上述问题的在线求解。但是，过大的求解范围会显著增加计算的复杂度。因此，有必要发展面向非结构化场景的自动驾驶拖拉机路径规划方法，使拖拉机高效地绕过障碍物，在保障作业安全性的同时提高作业效率。

技术实现思路

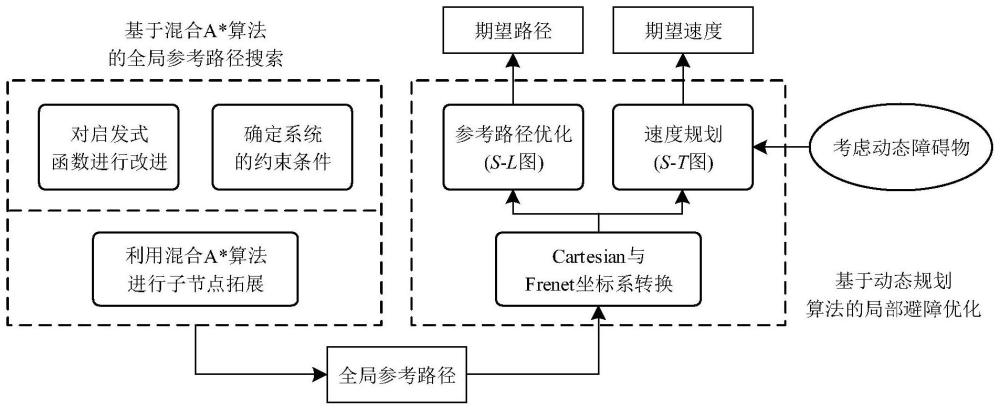
1、发明目的：针对现有技术中存在不足，本发明面向无车道线、无清晰的道路边界以及存在动态障碍物的农业机械作业场景，提出一种基于混合a*算法和动态规划算法的全局参考路径搜索和局部避障规划方法，旨在解决面向非结构化场景的自动驾驶拖拉机路径规划问题。首先，基于混合a*算法确定满足拖拉机运动学约束的全局参考路径，在考虑拖拉机动力学约束和静态障碍物的情况下完成最优参考路径搜索。在此基础上，利用动态规划算法对参考路径的曲率进行平滑，并结合动态规划算法完成针对动态障碍物的速度规划。

2、技术方案：

3、本发明提供一种面向非结构化场景的自动驾驶拖拉机路径规划方法，该方法包括以下步骤：

4、s1.建立环境地图模型；确定静态障碍物所处的具体位置；

5、s2.利用reeds-shepp曲线模型对启发式函数进行改进，得到混合a*算法的代价函数；

6、s3.确定系统的约束条件，保证避障安全性，并适应拖拉机运动特性；

7、s4.根据步骤s2代价函数与步骤s3的系统约束进行子节点拓展，获取全局参考路径；

8、s5.进行基于动态规划算法的局部避障优化之前，将拖拉机位姿信息进行frenet坐标与cartesian坐标转换；

9、s6.根据步骤s4获得的全局参考路径以及步骤s5的坐标转换方法，利用s-l图对全局参考路径进行优化，并获得连续、平滑的期望路径；

10、s7.由步骤s5的坐标转换方法以及步骤s6的期望路径规划结果，利用s-t图进行速度规划，确定有效规避动态障碍物的期望速度。

11、进一步地，所述步骤s1的具体方法是：

12、建立栅格地图，将拖拉机工作环境离散化为多个独立的正方形栅格，每个栅格对应真实工作环境中的一个具体位置，根据真实环境中的障碍物情况，将相应的栅格标记为占据或空闲状态，所有标记后的栅格共同构成环境地图模型；

13、在栅格地图中，被占据的栅格用黑色表示，在数值矩阵中对应的值为1；空闲的栅格用白色表示，在数值矩阵中对应的值为0，栅格地图的数学模型表示为：

14、

15、其中，a代表整个环境地图模型，m和p分别为环境地图栅格化后的行数和列数，aij表示位于(i,j)处的栅格，aij＝0表示栅格为空闲状态，即不存在障碍物；aij＝1表示栅格被占据状态，即存在障碍物。

16、进一步地，所述步骤s2的具体方法是：

17、a*算法核心思想是利用启发式函数对算法遍历的方向进行引导，并根据代价函数f(n)评估网络的每个节点，具体可表示为：

18、f(n)＝g(n)+h(n,g)(2)

19、其中，g(n)为起始节点到当前节点的实际代价，h(n,g)为当前节点n到目标节点g的距离启发式函数，用于评估当前节点n到目标节点g的预测距离代价；

20、搜索过程中，相应的距离启发式函数h(n,g)采用欧几里得距离h1(n,g)，以忽略拖拉机非完整性约束、考虑避障环境约束：

21、

22、其中，(xn,yn)为当前节点n的坐标，(xg,yg)为路径目标点的坐标；

23、reeds-shepp曲线模型由两个转弯和一段直线组成，用于确定拖拉机或其他运动体在给定约束条件下的最短路径，利用a*算法常用的距离启发式函数和reeds-shepp曲线模型进行并行设置，得到混合a*算法，即选取其中较大的值作为搜索的启发式函数值，同时满足拖拉机的非完整运动学约束和通行效率最高：

24、h(n,g)＝max(h1(n,g),h2(n,g))      (4)

25、其中，h2(n,g)表示采用reeds-shepp曲线模型的距离启发式函数，在忽略环境障碍、考虑拖拉机非完整性约束的条件下获得从当前节点到达目标位置的最短路径；

26、混合a*算法中，每个节点都记录其父节点拓展到当前节点的特定速度与前轮转角，为防止车速v和前轮转角δf频繁变化，在实际代价g(n)中添加附加的代价函数g1(n)：

27、g1(n)＝ωg1·|vn-vn-1|+ωg2·|δfn-δfn-1|       (5)

28、其中，ωg1为汽车行驶状态发生改变时的权重系数；ωg2为汽车行驶方向改变时的权重系数；vn为汽车行驶到当前节点n时的车速，vn-4为汽车行驶到前一个节点n-1时的车速，δfn汽车行驶到当前节点n时的前轮转角，δfn-1为汽车行驶到前一个节点n-1时的前轮转角。

29、进一步地，所述步骤s3的具体方法是：选择矩形和多边形作为拖拉机与障碍物的轮廓，将拖拉机视为矩形，利用拖拉机边界函数来描述拖拉机尺寸和形状，相应的四个顶点m1～m4横纵坐标表示为：

30、

31、其中，(x,y)为拖拉机位置坐标，f为拖拉机前悬距离、r为拖拉机后悬距离、l为拖拉机轴距、w为车身宽度拖拉机尺寸参数、ψ为拖拉机航向角；

32、判断拖拉机与障碍物是否发生碰撞，需要确定拖拉机边界和障碍物轮廓是否重合，采用三角形面积法检验拖拉机顶点坐标与凸多边形n1n2…nn的位置关系，令拖拉机其中一个顶点坐标为mi，连接点mi与凸多边形的每两个相邻顶点构成三角形，并将这些三角形的面积进行累加，若累加得到的面积之和大于凸多边形的总面积，则确定点mi位于凸多边形的外部；若面积之和小于等于凸多边形的总面积，点mi可能位于多边形的内部，如式(7)所示：

33、

34、其中，s代表各个多边形的面积；

35、凸多边形面积可通过若干个三角形进行求解，在二维平面上，碰撞一定会发生在顶点处，将车身矩形的每个顶点始终约束在障碍物多边形的外部，同时限制多边形障碍物的每个顶点也位于车身矩形的外部，利用式(7)，得到点mi位于凸多边形n1n2…nn外部的约束条件f1与f2，并建立如下的避障约束：

36、

37、其中，γ(n1,…nn)为凸多边形顶点的集合，χ(m1,…m4)为车身矩形四个顶点的集合；根据拖拉机的运动学特性，可知拖拉机行驶的路径曲率κ仅与前轮转角δf有关：

38、

39、过大的前轮转角会使路径曲率增大，在降低行驶舒适性同时会加剧拖拉机的机械磨损，因此通过限制拖拉机前轮转角，以约束规划路径的曲率：

40、|δf|≤arctan(lκmax)      (10)

41、最终确定混合a*算法求解的避障约束与前轮转角约束，保证避障安全性，并适应拖拉机运动特性。

42、进一步地，所述步骤s4的具体方法是：考虑拖拉机的运动学约束，采用混合a*算法改变节点的拓展方式：每个节点均包含拖拉机的状态信息(x,y,ψ)，其中x和y表示拖拉机的位置坐标，ψ表示拖拉机的航向角，每个节点以中心点表示父节点，混合a*算法的子节点数量为6，从位于栅格中的任意位置生成，节点之间以三维运动学状态连接，且搜索出的路径能够满足拖拉机的非完整性约束，即利用混合a*算法规划求解得到全局参考路径。

43、进一步地，所述步骤s5的具体方法是：将步骤s1-s5中采用cartesian坐标系进行道路描述转换为采用frenet坐标系进行描述，cartesian坐标系下，某一点的拖拉机运动状态表示为[x,y,v,ψ,a,κ]；a是cartesian坐标系下的纵向加速度，而在frenet坐标系下，拖拉机运动状态表示为其中，s为纵向位移，为纵向车速，为纵向加速度，为横向车速，为横向加速度，l′为l对s的导数，l″为对的导数；

44、cartesian坐标系转frenet坐标系的公式为：

45、

46、frenet坐标系转cartesian坐标系的公式为：

47、

48、其中，sr为期望纵向位移，xr和yr为cartesian坐标系下期望横向位置和纵向位置，κr为参考路径曲率，κ′r为参考路径曲率对s的导数，δψ＝ψ-ψr，ψr为参考航向角。

49、进一步地，所述步骤s6的具体方法是：首先，根据场景中的障碍物信息构建frenet坐标系下的表示道路与障碍物之间的关系图，简称s-l图，通过在s-l图中撒点并初始化将空间离散化；其次，设置成本函数，为每个节点分配一个代价值以描述相邻单元之间的路径选择关系；考虑障碍物的位置、拖拉机的当前位置和目标位置，采用动态规划算法对参考路径进行优化，确保在避免碰撞的同时能够找到最小代价路径，代价函数j由路径与静态障碍物的安全距离代价函数jobs、平滑性代价函数js以及偏离参考路径程度代价函数jl描述：

50、j＝jobs+js+jl        (13)

51、路径与静态障碍物的安全距离代价函数jobs表示为：

52、

53、其中，dmax为最大碰撞距离，dmin为最小碰撞距离，[dmin,dmax]为碰撞缓冲区间，frisk为单调递减的碰撞风险函数，越靠近障碍物，frisk值越大，即越容易发生碰撞风险；

54、平滑性代价函数js表示为：

55、

56、其中，t0为路径规划开始时间，ts为路径规划结束时间，ω1、ω2、ω3为平滑性权重系数，分别代表路径横向位移、路径曲率以及路径曲率的变化率，l″′为对的导数；

57、偏离参考路径程度的代价函数jl可以表示为：

58、

59、其中，ωl为偏离参考路径程度权重系数，lr为参考线函数；

60、采用递推的方法从起点到终点进行搜索，通过计算每个节点到终点的最小代价值来更新当前节点的代价值，并保存路径信息以供回溯，在所有节点计算完毕之后，筛选得到所有路径采样节点的最小连接代价；

61、然后利用五次多项式对给定的节点进行插值和拟合，将离散节点连续化，得到符合要求的平滑路径曲线，五次多项式曲线可以通过以下公式表示：

62、

63、其中，t代表时间，a10～a(n-1)5代表五次多项式的系数，τ(s)代表多段五次多项式的集合，s5代表s的五次方，假设起点状态信息为[sj,lj,l′j,l″j]，终点状态信息为[sk,lk,l′k,l″k]，将起点与终点状态信息带入式(17)，得：

64、

65、其中，ak0～ak5代表每一段五次多项式系数；

66、求解式(18)的线性方程组，可确定五次多项式曲线的所有系数，实现对参考路径的优化；最后，对该路径的节点信息进行坐标转换，将相关位置坐标信息由frenet坐标系的s-l图变换到cartesian坐标系下的x-y图，获取用于跟踪控制的期望路径。

67、进一步地，所述步骤s7的具体方法是：记动态障碍物切入的时刻为tin，切出的时刻为tout，长度s1s2与动态障碍物的宽度有关，s-t图的构建依赖于对动态障碍物轨迹的预测，采用恒速度模型对动态障碍物的轨迹进行预测：

68、

69、式中，障碍物初始位置为(s0,l0)，横纵向速度分别为和(st,lt)为t时刻的障碍物预测轨迹；

70、将动态障碍物投影到s-t图上，并在s-t图中采样，采样过程中，每个时刻都会产生一系列采样点，即多个待选解，为得到最优解，需定义一个代价函数来评价各个待选解的优劣，安全性指拖拉机在速度规划过程中应尽可能与动态障碍物保持安全距离，以确保行驶的安全，在存在障碍物的时间区间内，引入一个安全性代价函数j1：

71、

72、其中，ωobs为障碍物权重系数，正数kb表示拖拉机远离动态障碍物的程度，sobs表示直线拟合动态障碍物形成的边界，sb表示拖拉机移动的边界；如果在某个时间段内，拖拉机受到多个动态障碍物的影响，将多个安全性代价函数j1进行累加；

73、为使拖拉机的速度和速度变化率尽量小，设置舒适性的代价函数j2：

74、

75、其中，ωv和ωa分别表示速度和速度变化率的权重系数；

76、期望速度vref不考虑移动障碍物影响，由道路限速、路径曲率以及其他交通规则决定，定义期望速度代价函数j3：

77、

78、其中，ωr表示与期望速度偏离的权重系数；

79、整合上述代价函数，得到速度规划的代价函数：

80、j＝j1+j2+j3(23)

81、最后，利用动态规划算法在s-t图中求解出一条代价最低的速度曲线，以确定拖拉机在面对动态障碍物时的速度决策方式；将相关位置速度信息由frenet坐标系的s-t图变换到cartesian坐标系下的x-y图，获取有效规避动态障碍物的期望速度。

82、本发明的有益效果为：

83、(1)提出混合a*算法，针对静态障碍物进行全局参考路径搜索，得到满足电动拖拉机运动学约束、由起点到终点的最优路径。

84、(2)基于s-l图完成参考路径优化，基于s-t图完成速度规划，实现考虑动态障碍物的局部避障优化。