一种欠驱动水面航行器轨迹跟踪滑模控制方法

本发明涉及欠驱动水面航行器轨迹跟踪控制方法领域，具体是一种欠驱动水面航行器轨迹跟踪滑模控制方法。

背景技术：

1、我国作为海洋大国，对自由进入海洋空间、维护海洋空间权益、加强对海洋空间管控等能力十分重视，无人水面航行器得到大力发展。此外，在农业机械领域，无人水面航行器可应用于复杂水域环境的资源调查与监测，自动采收，替代人类进行涉水劳动，有助于农业的自动化、智能化、可持续的发展。综合考虑安全、经济以及特殊任务要求，无人机水面航行器必须按既定路线航行，例如埋设水雷、海洋监测和农用水塘自动采收等。水面欠驱动航行器是一类具有非线性特性的系统，由于欠驱动航行器建模的不确定因素，加之复杂的环境的扰动，使得欠驱动航行器航行时的参数摄动更加复杂。使欠驱动航行器系统成为一类特殊的非线性系统，欠驱动航行器的轨迹跟踪控制设计面临很多局限。

2、传统的轨迹追踪控制方法是通过系统的局部线性化或多变量模型解耦，利用状态反馈法、模型预测控制法(model predict control，mpc)、滑模控制法（sliding modecontrol，smc）等。现有的，一种航标船抗干扰轨迹跟踪控制方法，专利号为cn202010976786.6，记载了采用梯度动量下降法，计算径向基函数阈值向量的更新值，而对于梯度动量下降法的问题而言：

3、1.不能保证全局收敛（全局最优），梯度下降算法针对凸优化问题原则上是可以收敛到全局最优的，因为此时只有唯一的局部最优点。而实际上深度学习模型是一个复杂的非线性结构，一般属于非凸问题，这意味着存在很多局部最优点（鞍点），采用梯度下降算法可能会陷入局部最优。

4、2.适当的学习速率选择困难，学习速率过小时收敛速度慢，而过大时导致训练震荡，而且可能会发散，目前可采用的方法是在训练过程中调整学习率大小。

5、3. 当有多个参数需要求解时，学习速率对于每个参数都相同，这种做法是不合理的：如果训练数据是稀疏的，并且不同特征的出现频率差异较大，那么比较合理的做法是对于出现频率低的特征设置较大的学习速率，对于出现频率较大的特征数据设置较小的学习速率。会导致神经网络估计效果变差，计算径向基函数阈值向量的更新值的计算效率低，计算结果精确度不高。

6、所以，进行一种欠驱动水面航行器轨迹跟踪滑模控制方法的设计，能够解决欠驱动水面航行器的传统轨迹跟踪控制方法控制精确度不高、耗时低效，rbf神经网络滑模控制应用在欠驱动水面航行器的轨迹跟踪控制领域产生的设计参数多，人为调整困难，设计复杂的技术问题；同时保证求解全局收敛（全局最优），对多个参数求解时，学习速率更快更易实现。

技术实现思路

1、本发明的目的在于提供一种欠驱动水面航行器轨迹跟踪滑模控制方法，它可以减少人工调试时间，进一步提升系统的响应速度，通过神经网络滑模控制，使航行器快速跟踪上期望轨迹，并且能够对系统中的不确定性项进行有效估计。跟踪过程中的误差能被有效控制在更小范围内，同时确保了整体追踪过程的平滑性，展现出了较强的抗干扰能力。

2、本发明为实现上述目的，通过以下技术方案实现：

3、一种欠驱动水面航行器轨迹跟踪滑模控制方法，其特征在于：包括下述步骤：s1，基于欠驱动水面航行器上所设置的位置传感器进行自我定位，并将自我位置信息进行定位处理；

4、s2，根据自我定位信息进行欠驱动水面航行器位置信息数学模型的建立，并对神经网络滑膜控制器进行设计；

5、s3，引入鹦鹉优化算法到s2步骤中的神经网络滑膜控制器，用于选择rbf神经网络的参数，减少人工调试时间，提升系统响应速度和精确度；

6、s4，随机生成一组预定义的候选解群体，再引入切换步长因子及可控变化概率对s3中的初始鹦鹉算法进行改进；

7、s5，将改进后的鹦鹉优化算法应用于rbf神经网络的参数最优选择中，确定并选择个体最优和全局最优；

8、s6，将改进后的算法应用到欠驱动水面航行器的控制系统，实现欠驱动水面航行器的轨迹跟踪控制。

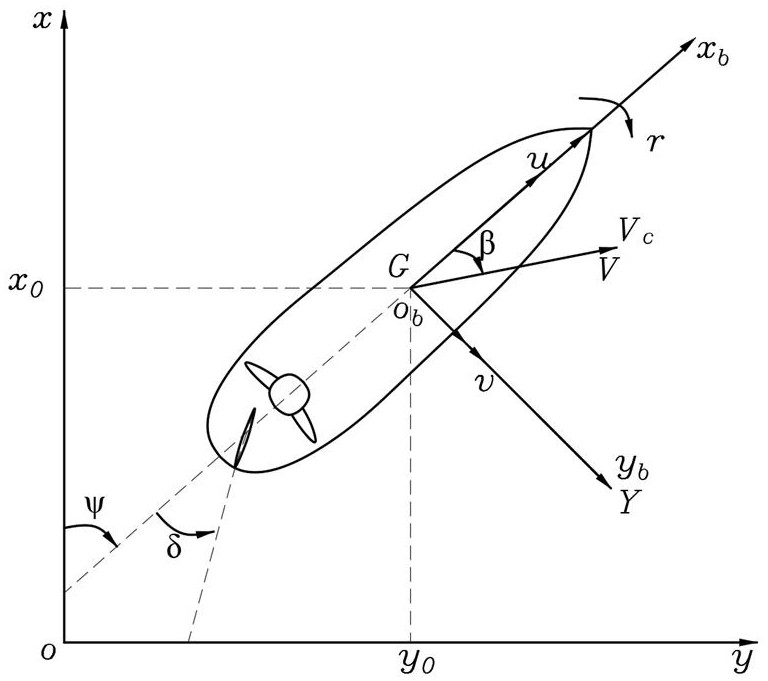
9、所述s2中的数学模型建立考虑的前向、横漂、艏摇三自由度的水平面运动，构建的数学模型公式为：

10、；

11、式中：分别为航行器在惯性坐标系中的前进、横漂两个方向上的位移及偏航角；分别为附体坐标系下船舶的前进、横漂两个方向上的速度及偏航方向的角速度，表示己知附加质量，引入欠驱动水面航行器模型不确定项为的两个控制信号，分别代表控制力和控制力矩；表示在外界的未知时变干扰。

12、结合数学模型，所述s2步骤中神经网络滑膜控制器的转向控制率为：

13、；

14、其权值自适应律为：；

15、参数自适应律为：；

16、纵向控制率为：

17、；

18、其权值自适应律为：；

19、参数自适应律为： ；

20、式中，，为的先验估值，为的先验估值。

21、所述s3步骤中鹦鹉优化算法的公式如下：

22、初始化阶段：；

23、式中，表示范围内的随机数，；

24、觅食阶段：；

25、式中，表示当前位置，表示更新后的位置，表示当前种群内的平均位置，表示从初始化到当前搜索到的最佳位置，它也表示主人与食物的当前位置，t表示当前迭代次数，l(d)表示levy分布，用于描述鹦鹉的飞行情况，即算法的随机搜索路径；

26、停留阶段：

27、；

28、式中表示维度dim的全1向量，表示飞往宿主的过程，r (0,1)⋅ones(1,d)表示随机停在宿主身体某个部位的过程；

29、交流阶段：；

30、式中，y(t)是为简化表示引入的有关时间的函数，上式第一项表示个体加入鹦鹉群体进行交流的过程，第二项表示个体在交流后立即飞出的过程；位置更新后生成随机数r∈[0，1]，两种行为的使用在[0,1]范围内随机生成的p来实现；

31、怯生阶段：；

32、其中，表示重新定向飞向所有者的过程；

33、表示远离陌生人的过程。

34、所述s4中的切换步长因子表达式为：

35、；

36、式中，为第t+1轮和第t轮的搜索步长，q为现最佳解值；q`为位置更新后对比择优位置对应的目标解值；

37、所述可控变化概率表达式为：；

38、式中，为最大概率，为最大迭代次数；

39、且优化有的鹦鹉优化算法公式为：

40、。

41、对比现有技术，本发明的有益效果在于：

42、1.本发明采用鹦鹉优化函数去解决欠驱动水面航行器神经网络滑模控制设计参数过多，人为设计困难问题，而现有技术是通过最小参数学习法降低了设计参数量，但其仍需要人为设置固定参数，同时由于采用神经网络权值的上界估计、不等式放大的方法，导致控制算法过于保守，而采用鹦鹉算法对所有设计参数进行学习，动态寻求最优解，进一步提高 rbf神经网络对模型不确定项的逼近速度，使控制器进行更加快速、精确的轨迹跟踪控制。

43、2、本发明采用引入可控变化概率改进原始鹦鹉算法，原鹦鹉算法交流过程中保留最优解的概率无法随当前求解值优劣程度变化，无论解的优劣都会将以相同的可能性被替换为其它随机解，损失了一定的寻优效率。通过解决引入切换步长因子及可控变化概率提高最优解的留存概率。通过改进使概率能够与整个鹦鹉优化算法迭代过程适应关联，有助于平衡全局与局部的搜索，提升鹦鹉优化算法的灵活性。

44、3、本发明采用引入切换步长因子去解决算法搜索步长全程随机无法调节的问题，如采用小步长，神经元感知范围收窄，会缺乏多样性的同时系统的调节时间增大，搜索效率低；采用步长过大，搜索精度降低，协调能力弱，易陷入局部最优解。本文提出一种切换步长因子对其鹦鹉优化优化算法的觅食行为过程进行控制，而现有技术中还没有解决该问题。自适应调整算法在觅食行为阶段的搜索步长大小。前期求解函数迅速收敛时，切换步长因子会根据表达式自适应增大，将鹦鹉优化算法的觅食搜索过程维持在大步长状态；当求解函数进行到后期缓慢收敛时，鹦鹉优化算法的觅食搜索过程步长会受控减小，提高全局最优值的发现概率，进而提升控制方法的精确度。

45、4、本发明采用鹦鹉优化算法去解决多个参数求解的问题，现有梯度下降法有多个参数需要求解时，学习速率对于每个参数都相同，会导致求解精确度不高，不适合用于多参数求解。