基于最小角度粒子群优化的多目标卫星数传调度方法

本发明属于卫星通信，具体涉及一种基于最小角度粒子群优化的多目标卫星数传调度方法。

背景技术：

1、在卫星通信技术领域，数传任务的难点是最小化传输时间和最大化任务完成集合的优先程度。数传问题涉及在有限的地面站资源下，对运行在我国上空的多颗卫星进行合理的调度。数传问题主要涉及以下挑战：建立合理的模型以利用有限时间窗口进行高效数据传输，合理分配地面站资源以满足更多卫星的数据传输需求，以及在最短时间内传输更多优先级高的卫星，从而最大化卫星和地面站的优先级，并缩短传输时间。

2、现有数传问题调度系统常存在数据传输效率低和可用资源分配不均的问题。可用资源包括卫星和地面站，且地面站数量有限，而待传输卫星数量众多，地面站的数量远远小于卫星。现有调度系统可能无法确保每个卫星都能获得足够的传输机会，导致优先级低的卫星长时间得不到传输，而优先级高的卫星也可能因资源分配不均而无法及时传输，这不仅浪费了有限的地面站资源，还可能影响卫星数据传输的及时性和准确性。群体智能优化方法，如粒子群优化算法等，已成为解决复杂大规模优化问题的有效工具。然而，传统群体智能优化方法可能在新问题中陷入局部最优解，且在处理复杂、多峰的优化问题时，需要对问题进行编码和解码，这可能会增加算法的难度和复杂度。

技术实现思路

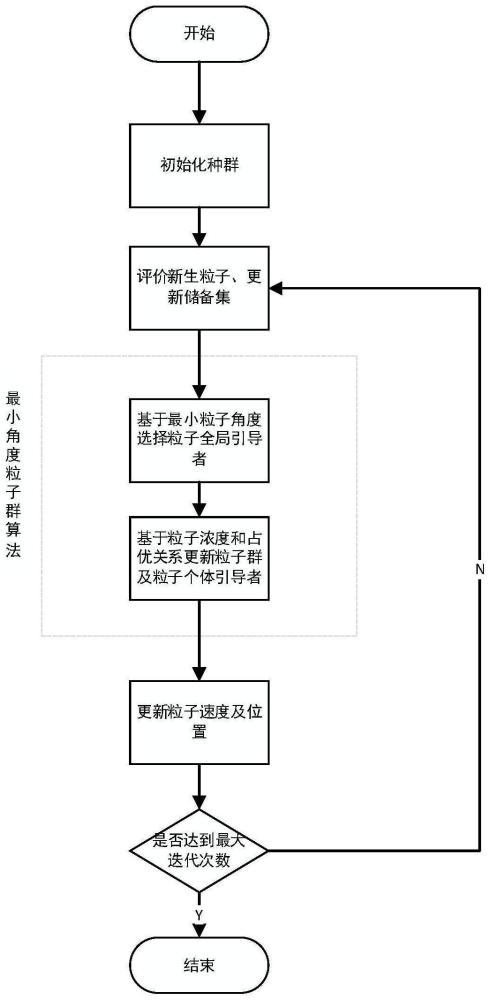
1、为了解决现有技术中存在的问题，本发明提供一种基于粒子群算法的卫星数传问题调度解决方案。该方法基于最小角度粒子群优化方法，旨在建立清晰的问题模型，实现快速测试，生成合理的规划方案。

2、为了实现上述目的，本发明采用的技术方案是：基于最小角度粒子群优化的多目标卫星数传调度方法，包括以下步骤：

3、结合地面站模型和卫星模型建立卫星数传调度问题决策变量模型；包括：基于粒子群算法，

4、采用二进制编码方式表示每个卫星是否被选择，选择对应二进制数中的1，不选择对应0：

5、

6、

7、tk,i,s,u：目标i的第u个可见时间窗口被地面站设备k数传的实际开始时间   (3)

8、tk,i,e,u：目标i的第u个可见时间窗口被地面站设备k数传的实际结束时间   (4)

9、根据卫星数传调度问题决策变量模型建立约束条件模型；

10、解算所述约束条件模型得到数传问题规划结果。

11、进一步的，地面站模型的构建包括：确定地面站设备集合res＝{r1,r2,…,rm}，设备数量为m；地面站设备k的优先级由其负责传输的卫星集合i决定，表示为gki，其中地面数传设备k在状态转换时所需的时间为：tchak；每个设备、卫星、时间窗口编号以及时间窗口的开始、结束和长度信息由集合ck,i,u＝{k,i,u,tk,i,s,u,tk,i,e,u,tk,i,l,u}表示，地面站设备k在第u个可见时间窗口内能传输的所有卫星集合表示为rmk,u。

12、进一步的，卫星模型构建包括：对于卫星i，其优先级表示为：pik，其中k∈res，示该卫星i正在由地面站设备k进行数据传输；卫星i的数据传输时长需求为mdi；调度周期的起始时间为ts，结束时间为te，整个调度的时间范围为[ts,te]；待传输的目标集合表示为：m＝{m1,m2,…,mn}，其中n为目标数量；待数传卫星i在第u个可见时间窗口内能接收来自所有地面站设备集合表示为mri,u。

13、4.根据权利要求3所述的基于最小角度粒子群优化的多目标卫星数传调度方法，其特征在于，建立卫星模型中式(1)～式(14)中，设置时间范围为[04:00,23:00]，地面站数量为4，卫星数量为12。

14、5.根据权利要求1所述的基于最小角度粒子群优化的多目标卫星数传调度方法，其特征在于，根据卫星数传调度问题决策变量模型建立约束条件模型时，约束条件包括：

15、1.所有的地面站设备在进行卫星数据传输问题时，必须在卫星与地面站设备之间的时间窗口内进行，否则提前开始或超出预定时间，都将视为违反操作规则；

16、

17、2.数据传输的成功完成需要实施数据传输的时间窗口持续时间满足或超过所需的数据传输跟踪持续时间要求；

18、

19、3.设备转换所需的最短时间限制；

20、

21、then tk,m,e,u+tchak+mdn≤tk,n,s,q                           (8)

22、4.数据传输问题中，实际传输时间必须达到或超过所需传输持续时间；

23、

24、5.在预定的规划时间范围内，每个目标只能被传输一次；

25、

26、6.同一地面传输设备只能对一个卫星的特定可见时间窗口进行数据传输；

27、

28、

29、7.同一卫星不能有超过一个地面站设备同时进行数据传输；

30、

31、

32、进一步的，解算所述约束条件模型得到数传问题规划结果包括：

33、创建一个种群xn＝(x1,x2,…,xn),其中每个粒子的位置在搜索空间内随机初始化；

34、对种群中每个粒子的适应值进行评估，评估时，目标函数由f1和f2组成，分别表示优先级高的卫星传输数量和数据传输时间的最小化，随后，基于评估结果更新粒子群算法的外部储备集：

35、

36、f2＝min(t)                          (16)

37、采用公式(17)从储备集中选取与粒子直线夹角最小的元素作为全局引导者；

38、

39、使用公式(18)和(19)更新粒子的位置和速度：

40、vi,j(t+1)＝wvi,j(t)+c1r1(xpi,j(t)-xi,j(t))+c2r2(xgj(t)-xi,j(t))  (18)

41、xi,j(t+1)＝xi,j(t)+vi,j(t+1)                            (19)

42、当达到最大迭代次数后，将所有可行的规划方案输出给用户。

43、进一步的，创建一个种群xn＝(x1,x2,…,xn)时，设定初始时刻每个粒子的速度为零，并给学习因子c1,c2赋值为1.49，

44、进一步的，初始化种群时，设置迭代此次为100次，设置惯性权重w1为1.2，学习因子c1＝1.5，c2＝1.5。

45、进一步的，在储备集中选取与粒子直线夹角最小的元素作为全局引导者的过程中，选择来自引导库a的元素a；i,j＝1,2,…,a作为全局导向角色的粒子群，记作x；(i＝1,2,…,n)，定义为一个特定元素a的子群集，所述子群集中的粒子数量称为粒子的浓度，浓度随着子粒子群中包含的粒子数目的增加而上升，粒子数减少则浓度降低，浓度这一概念的量度范围在零到最大值之间变动，在粒子的自我更新过程中，如果新生成的粒子相对于原粒子表现出优越性，即存在优势关系，根据所述优势关系来挑选粒子的局部引导者，通过划分多个子粒子群并计算每个子群中的粒子数量以确定各自的浓度，利用粒子的浓度和优势关系，进行粒子群以及粒子局部引导者的双重更新操作。

46、进一步的，评估个体并更新外部储备集时，设置外部储备集大小为20，如果pbest中个体和新个体互相不支配，将采用随机选择的方法，以0.5的概率去更新pbest，0.5的概率不更新pbest。

47、与现有技术相比，本发明至少具有以下有益效果：本发明面向卫星数传调度任务，通过对卫星数传任务的模型构建，以最大化卫星和地面站的优先级和最小化传输时间为任务目标，设计高效的改进粒子群优化方法，本发明所述方法能够有效跳出局部最优解，提高求解质量，并缩短求解时间，能提高卫星数传任务的效率和精度，对于卫星通信系统任务调度具有重要的实际意义；在方法验证阶段，实施例的实验结果验证本发明在不同任务规模的性能，说明本发明在数传问题上的泛化能力和适应能力。