一种基于高斯混合变分图自编码器的聚类方法

本发明涉及数据处理，尤其涉及一种基于高斯混合变分图自编码器的聚类方法。

背景技术：

1、随着科学技术的不断发展，大数据的产生与应用呈现出爆炸性增长的趋势，这其中包括了各种类型的高维度和高稀疏性数据，如基因组学、蛋白质组学、社交网络、互联网信息等。这些数据的维度高、稀疏性强、噪声高，给数据挖掘与分析带来了巨大挑战，尤其是对于聚类分析而言。聚类是一种重要的数据分析方法，其目标是将数据点分成不同的组或簇，使得同一组内的数据点相似度高，不同组之间的数据点相似度低。聚类是处理未标记数据的有效方法，它的应用涵盖各种领域，包括生物信息学、计算机视觉和社交网络分析等领域。

2、近年来，深度学习的快速发展为聚类分析提供了新的思路，其强大的特征学习能力和非线性建模能力使得对复杂高维数据的聚类更加准确和有效，深度嵌入聚类在高维度数据聚类研究中得到成功应用。深度聚类方法将降维过程与聚类同时进行，并通过使用辅助目标分布学习高度可信的分配来得到更准确的聚类结果。文献“clustering single-cell rna-seq data with a model-based deep learning approach”通过基于零膨胀负二项模型(zinb)的自编码器来学习数据的低维表示，并使用kl散度在潜在空间上执行聚类任务，实现降维的同时直接优化聚类。文献“atopology-preserving dimensionalityreduction method for single-cell rna-seq data using graph autoencoder”构建图并使用面向多任务的图自编码器来同时保存数据中的拓扑结构信息和特征信息。

3、现有方法大多使用的模型是基于自编码器的聚类模型，或者是基于图自编码器的聚类模型。基于自编码器的聚类模型忽略了节点与节点之间的结构关系，这种结构信息对于揭示节点间的相似性具有重要作用，帮助模型得到更准确的聚类结果。图自编码器无法学习数据低维表示的分布，因此导致学习到的低维表示不稳定或低质量，无法获得更准确的聚类结果。

技术实现思路

1、本发明要解决的技术问题是针对上述现有技术的不足，提供一种基于高斯混合变分图自编码器的聚类方法，能够有效学习到数据的特征信息和结构信息，发现复杂数据的分布，获取低维表示的聚类信息，捕获数据的全局概率结构。

2、为解决上述技术问题，本发明所采取的技术方案是：

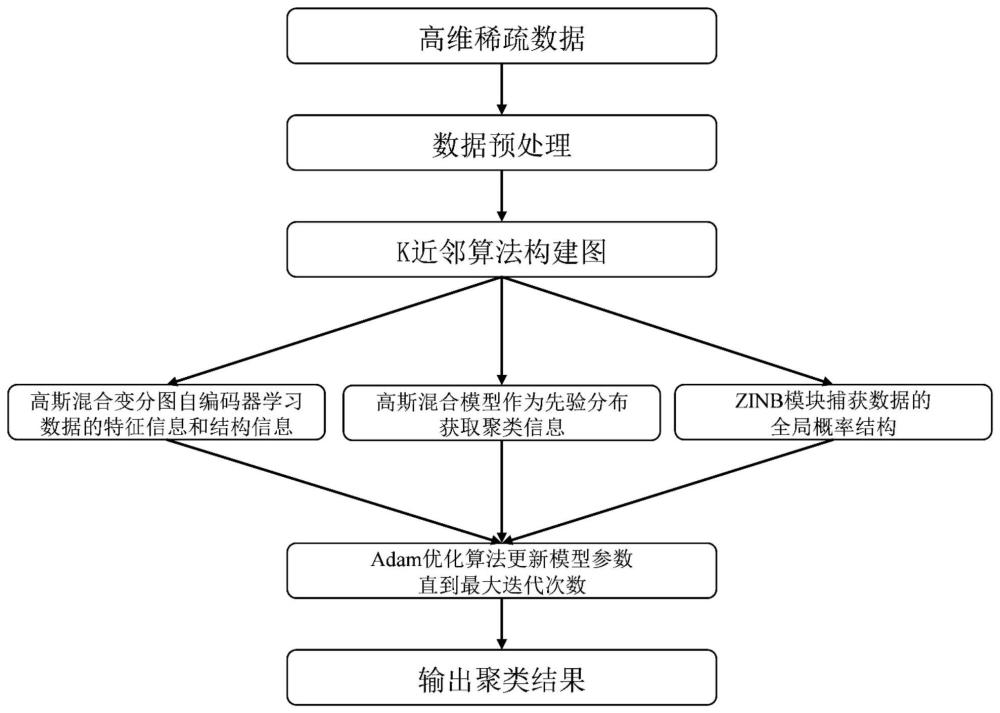
3、一种基于高斯混合变分图自编码器的聚类方法，以变分图自编码器为基础框架，并使用高斯混合模型作为变分图自编码器的先验分布，然后将zinb模型集成到改进的变分图自编码器中学习高维稀疏数据的均值、离散度和数据丢失的概率，其中数据丢失的概率即真实数据被观测为0的概率，得到数据的有效特征表示；具体包括以下步骤：

4、步骤1：对高维稀疏数据进行数据预处理；

5、步骤2：使用k近邻算法对数据构建图，得到邻接矩阵；

6、步骤3：通过高斯混合变分图自编码器学习数据的低维潜在表示，变分图自编码由编码器和解码器组成，高斯混合模型作为变分图自编码器的先验，能够发现复杂的高维稀疏数据的分布，并学习低维表示中固有的聚类信息；特征解码器和图解码器将低维潜在表示转换为数据的原始特征矩阵和邻接矩阵，从而实现数据的重构；同时将零膨胀负二项模型集成到高斯混合变分图自编码器中来学习高维稀疏数据的全局概率分布；使用adam优化算法来更新模型的参数，并获得数据的有效特征表示z；

7、步骤4：将高斯混合模型应用于学习到的低维表示中能学习固有聚类信息，直接从最后优化的聚类分配分布中得到聚类结果。

8、进一步地，所述步骤1的数据预处理具体包括：

9、步骤1.1：对数据进行过滤和质量控制；

10、步骤1.2：对特征矩阵进行标准化处理，离散数据经过平滑处理，并通过自然对数转换进行重新缩放，标准化公式如下：

11、

12、其中，xij表示数据的特征矩阵x中第i行第j列的元素，m(x)表示整个数据特征矩阵的中位数；∑oxio是对x中第i行所有元素求和；

13、步骤1.3：数据标准化之后，对高维稀疏数据中的特征进行筛选保留，最大限度保留数据中的潜在信息；

14、对数据进行特征选择，保留数据中前500个高度可变的特征，以保留高维数据中最具有信息量的部分。

15、进一步地，所述步骤2的具体方法为：

16、步骤2.1：k近邻算法中的邻居数量k取值为10；

17、步骤2.2：使用欧式距离计算每个节点与其最近邻节点之间的相似度，欧式距离计算公式如下：

18、

19、其中，p和q是数据集中的两个节点，它们在高维空间中的坐标分别为(p1,p2,...,pn)和(q1,q2,...,qn)；

20、步骤2.3：基于相似度计算结果构造图，采用无向图的形式来表示节点之间的关系，每条边的权重统一设置为1；

21、无向图表示为g＝{v,e,x}，其中v＝{v1,v2,…,vn}是节点的集合，x＝{x1,x2,…,xn}∈rn×d是数据的特征矩阵，每个xi∈rd表示每个节点的特征向量；e＝{eij}则表示数据中节点之间边的集合；使用邻接矩阵a＝{aij}∈rn×n来表示节点图，其中，如果(vi,vj)∈e，则aij＝1，否则aij＝0。

22、进一步地，所述步骤3具体包括以下步骤：

23、步骤3.1：初始化模型参数；

24、步骤3.2：对模型进行训练，训练过程包括预训练和正式训练两个过程；

25、步骤3.2.1：预训练阶段利用高斯混合模型对模型的先验参数进行初始化；

26、步骤3.2.2：正式训练阶段中高斯混合变分图自编码器学习数据的特征信息和结构信息，获取低维潜在表示；

27、步骤3.3：在学习到的低维表示上施加高斯混合分布，高斯混合模型学习低维表示中固有的聚类信息，根据变分贝叶斯推理，通过最大化生成的数据的对数似然来进行模型优化；公式如下所示：

28、

29、其中，log p(a,z,c)表示数据的对数似然，a是邻接矩阵，z是模型学习到的低维表示，c是数据中样本的类别；

30、步骤3.4：通过推导得到模型训练的变分证据下界即elbo，并通过最大化变分证据下界进行优化，公式如下所示：

31、

32、其中，表示模型训练的变分证据下界，等式右边第一项是重构损失，它表示的含义是：首先从变分后验分布q(z,c|x,a)采样隐变量即模型学习到的低维表示z和类别变量c，然后计算给定隐变量z的情况下生成的对数概率则表示在变分后验分布q(z,c|x,a)下对此对数概率进行加权平均操作，表示生成数据和真实数据之间的期望差异；等式右边第二项是高斯混合先验p(z,c)到变分后验q(z,c|x,a)的kl散度，它表示模型在学习过程中通过变分推断得到的分布和真实数据的分布之间的距离；

33、步骤3.5：特征解码器和图解码器将模型学习到的低维潜在表示转换为数据的原始特征矩阵和邻接矩阵，从而实现数据的重构，学习数据中的每个节点的特征信息和节点之间潜在的关系；

34、步骤3.6：将零膨胀负二项模型集成到高斯混合变分图自编码中，学习高维稀疏数据的均值、离散度和数据丢弃的概率以更好的捕获数据的全局概率结构；

35、步骤3.7：使用adam优化算法来更新模型的参数；损失函数包括重构损失、elbo和zinb损失，通过最小化损失函数，优化编码器和解码器的权重与偏置。

36、进一步地，所述步骤3.1具体包括：

37、步骤3.1.1：初始化编码器部分，包括创建图卷积对象；

38、步骤3.1.2：初始化解码器部分，包括特征矩阵解码器和邻接矩阵解码器的网络层；

39、步骤3.1.3：初始化模型的参数，包括隐藏单元维度、解码器层的维度、数据丢弃的概率和聚类数目；

40、步骤3.1.4：初始化先验分布的参数，包括聚类概率、均值和对数方差。

41、进一步地，所述步骤3.2.1的预训练中，使用高斯混合模型对变分图自编码器学习到的低维表示进行聚类，从而获得聚类中心和聚类权重作为模型的先验参数，用于初始化模型；预训练阶段结束后，评估模型并保存预训练阶段得到的模型参数。

42、进一步地，所述步骤3.2.2的具体方法为：

43、步骤3.2.2.1：进行编码器网络训练，将每个节点的特征数据转换为节点的隐变量；编码器的结构由两层图卷积神经网络组成，公式如下所示：

44、z(1)＝frelu(x,a∣w(0))

45、

46、

47、其中，x是高维稀疏数据的特征矩阵，a是邻接矩阵，z(1)是第1层的节点特征矩阵，w是与gcn层相关联的参数，μ和σ2分别表示对应高斯分布的均值和方差，并且

48、步骤3.2.2.2：通过重参数化技巧，从编码器网络的输出中进行采样，包括均值向量和方差向量，用于表示数据的潜在分布。

49、进一步地，所述步骤3.5的具体包括：

50、步骤3.5.1：特征解码器的将模型学习到的低维表示重构为原始特征矩阵；给定隐变量z的情况下，特征解码器的结构如公式所示：

51、

52、其中，为重构后的特征矩阵，dθ为解码器；特征解码器将低维表示z作为输入，通过多层的全连接神经网络来重建细胞的特征矩阵，特征重构损失如公式所示：

53、

54、其中，表示特征重构损失，n是数据中样本的数量；

55、步骤3.5.2：图解码器将低维表示重构为原始邻接矩阵，它通过隐变量z之间的内积来重建图数据，图解码器的结构如公式所示：

56、

57、其中，为重构的邻接矩阵，σ为sigmoid激活函数；

58、图重构损失通过应用交叉熵损失函数来衡量重构的邻接矩阵和真实的邻接矩阵a之间的差异，如下式所示：

59、

60、其中，表示图重构损失，aij和分别表示邻接矩阵a和中第i行第j列的元素。

61、进一步地，所述步骤3.6具体包括：

62、步骤3.6.1：在特征解码器添加三个全连接层神经网络来估计zinb模型中均值μ、离散度θ和数据丢弃概率π；

63、步骤3.6.2：定义zinb模型的损失函数为zinb分布的负对数似然，如公式所示：

64、

65、其中，表示zinb模型的损失函数，pzinb(x|π,μ,θ)表示给定数据丢弃概率π、均值μ和离散度θ参数的情况下数据x的概率密度函数。

66、进一步地，所述步骤4具体包括：

67、步骤4.1：将高斯混合模型应用于模型学习到的低维潜在表示中可以学习固有聚类信息，聚类分配分布定义为：

68、

69、其中，q(c|x,a)表示后验概率；p(g)表示样本类别c的先验概率；p(z|c)表示给定类别c的情况下隐变量z的条件概率分布；∑c′p(c′)p(z|c′)表示在所有可能的类别c′下，隐变量z的边缘概率分布的求和，确保后验概率总和为1；

70、步骤4.2：直接从最后优化的聚类分配分布中得到聚类结果，数据i的类别是使得后验概率值qic最大的类别c。

71、采用上述技术方案所产生的有益效果在于：本发明提供的基于高斯混合变分图自编码器的聚类方法，使用高斯混合模型作为变分图自编码器的先验分布，能够发现复杂数据的分布，直接获取低维表示中的聚类信息，从而以端到端的方式实现更好的聚类效果；本发明还将zinb模型集成到改进的变分图自编码器中，通过学习数据的均值，离散度、数据丢弃的概率三个特征分布参数，来捕获高维稀疏数据的全局概率结构，具备较高的聚类准确率，实现了较好的模型效果。