一种行星齿轮传动系统全局非线性损伤动力学建模方法

本发明涉及齿轮动力学，特别是涉及一种行星齿轮传动系统全局非线性损伤动力学建模方法。

背景技术：

1、齿轮传动是现代机械中应用最广泛的传动形式，行星传动以高效率、多传动比、负载能力强与结构紧凑等特点被广泛应用于汽车工业、船舶与海洋工程、机器人与航天航空等领域中。行星传动系统应用领域工作要求高，而行星传动系统工作过程中齿轮裂纹的产生不可避免，将裂纹齿轮时变啮合刚度引入行星齿轮传动系统动力学模型，研究行星齿轮裂纹对行星齿轮传动系统动力学特性的影响，对行星传动系统的设计、优化与寿命预测具有重要意义。现有技术缺少对行星齿轮传动系统全局非线性损伤动力学的研究方法。

2、为了解决上述问题，本发明提出了一种行星齿轮传动系统全局非线性损伤动力学建模方法，该方法构建含裂纹的行星齿轮传动系统模型，分析行星齿轮传动系统结构，确定轴承力、含裂纹的齿轮副时变啮合力，构建行星齿轮传动系统全局非线性损伤动力学模型，建立含裂纹的行星齿轮传动系统振动微分方程，通过数值求解系统方程，得到初始条件下系统动力学响应，采用胞映射法得到行星齿轮传动系统全局响应随激励频率与齿轮裂纹的演化规律，探究齿轮裂纹对系统全局非线性动力学的影响机理，并对系统参数进行优化。该方法既填补了含裂纹的行星齿轮传动系统相关技术空白，又具有较大的社会效益与经济效益。

技术实现思路

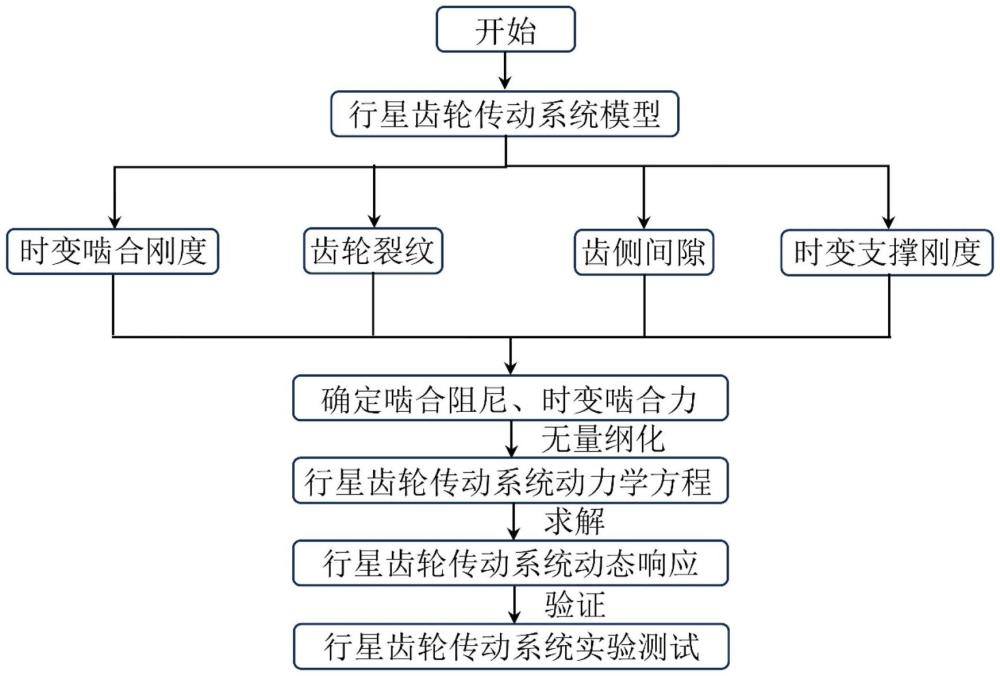
1、为了克服现有技术不足，填补相关技术空白，本发明提供了一种行星齿轮传动系统全局非线性损伤动力学建模方法，该方法构建行星齿轮传动系统模型，分析系统结构，确定轴承力、含裂纹的齿轮副时变啮合力，构建行星齿轮传动系统全局非线性损伤动力学模型，建立含裂纹的行星齿轮传动系统振动微分方程，通过数值求解系统方程，得到初始条件下系统动力学响应，采用胞映射法得到行星齿轮传动系统全局响应随激励频率与齿轮裂纹的演化规律，探究齿轮裂纹对系统全局非线性动力学的影响机理，并对系统参数进行优化。

2、本发明解决其技术问题所采用的技术方案如下：一种行星齿轮传动系统全局非线性损伤动力学建模方法，其特征在于：

3、步骤(1)：构建行星齿轮传动系统模型，行星齿轮传动系统由太阳轮、行星轮、轴承、内齿圈组成，各行星轮参数完全相同；

4、步骤(2)：轴承力为轴承滚动体与内外圈接触力合力，其沿x、y轴的分力fzx、fzy根据hertz接触理论可表示为：

5、

6、

7、其中，γ′i为轴承βi处受力变形后接触角，βi为滚动体转角，zb为滚动体个数，λ为滚动体变形量，球轴承指数n＝2/3，滚针轴承指数n＝9/10，kz为轴承支撑刚度；

8、步骤(3)：采用能量法求解裂纹齿轮时变啮合刚度：

9、

10、其中，f是齿轮啮合力，fa、fb分别为啮合力沿坐标轴x、y轴分力，ua是压缩势能，ub是弯曲势能，uh是赫兹接触变能，us是齿轮剪切势能，ka是轴向压缩刚度，kb是弯曲刚度，kh是赫兹接触刚度，ks是剪切刚度，b为齿轮齿宽，x为距离悬臂梁固定端的距离，hx为接触点到中线距离，e为杨氏模量，d为啮合点与基圆之间的距离；

11、不同裂纹长度和角度引起的截面积与截面转动惯量的变化，进而影响剪切刚度与弯曲刚度：

12、当hx<hr，hx>hr，α1<α3时:

13、

14、

15、当hx≥hr，α1>α3时:

16、

17、

18、其中，kb1、ks1分别为主动轮的弯曲刚度、剪切刚度，hr为齿顶宽度的一半，α为角度变量，α1为齿根圆齿基角，α2为基圆齿基角，α3为啮合角，α4为压力角，v为泊松比，l为裂纹长度，rb为基圆半径，b为齿轮齿宽，e为杨氏模量；

19、

20、其中，k为裂纹齿轮时变啮合刚度，ka1、ka2分别为主动轮轴向压缩刚度与从动轮轴向压缩刚度，kb1、kb2分别为主动轮弯曲刚度与从动轮弯曲刚度，ks1、ks2分别为主动轮剪切刚度与从动轮剪切刚度；

21、时变啮合力可沿坐标轴方向分解为fmx、fmy，其分力可表示为啮合线上等效振动位移与齿侧间隙非线性函数组成的复合函数：

22、

23、其中，rs为太阳轮分度圆半径，rp1为行星轮ⅰ分度圆半径，rp2为行星轮ⅱ分度圆半径，rp3为行星轮ⅲ分度圆半径，rr为内齿圈分度圆半径，xs为太阳轮振动位移沿坐标轴r方向的分量，xp1为行星轮ⅰ振动位移沿坐标轴x方向的分量，xp2为行星轮ⅱ振动位移沿坐标轴x方向的分量，xp3为行星轮ⅲ振动位移沿坐标轴x方向的分量，xr为内齿圈振动位移沿坐标轴x方向的分量，ys为太阳轮振动位移沿坐标轴y方向的分量，yp1为行星轮ⅰ振动位移沿坐标轴y方向的分量，yp2为行星轮ⅱ振动位移沿坐标轴y方向的分量，yp3为行星轮ⅲ振动位移沿坐标轴y方向的分量，yr为内齿圈振动位移沿坐标轴y方向的分量，θs为太阳轮振动角位移，θp1为行星轮ⅰ振动角位移，θp2为行星轮ⅱ振动角位移，θp3为行星轮ⅲ振动角位移，θr为内齿圈振动角位移，αn为压力角，xspi为太阳轮与行星轮i啮合线上等效振动位移，xpri为行星轮i与内齿圈啮合线上等效振动位移，espi(t)为太阳轮与行星轮i综合传动误差，epri(t)为行星轮i与内齿圈综合传动误差(i＝ⅰ、ⅱ、ⅲ)；

24、太阳轮与行星轮时变啮合力分力：

25、行星轮与内齿圈时变啮合力分力：

26、其中，t为时间变量，αn为压力角，k为裂纹齿轮时变啮合刚度，xspi为太阳轮与行星轮i啮合线上等效振动位移，xpri为行星轮i与内齿圈啮合线上等效振动位移，cspi为太阳轮与行星轮i啮合阻尼，cpri为行星轮i与内齿圈啮合阻尼，f(xspi)为太阳轮与行星轮i齿侧间隙非线性函数，f(xpri)为行星轮i与内齿圈齿侧间隙非线性函数(i＝ⅰ、ⅱ、ⅲ)；

27、步骤(4)：构建含裂纹的行星齿轮传动系统动力学模型，考虑以下23个自由度：

28、

29、其中，xs为太阳轮振动位移沿坐标轴x方向的分量，ys为太阳轮振动位移沿坐标轴y方向的分量，θs为太阳轮振动角位移，xzs为太阳轮轴承沿坐标轴x方向的振动位移，yzs为太阳轮轴承沿坐标轴y方向的振动位移，xp1为行星轮ⅰ振动位移沿坐标轴x方向的分量，yp1为行星轮ⅰ振动位移沿坐标轴y方向的分量，θp1为行星轮ⅰ振动角位移，xzp1为轴承ⅰ沿坐标轴x方向的振动位移，yzp1为轴承ⅰ沿坐标轴y方向的振动位移，xp2为行星轮ⅱ振动位移沿坐标轴x方向的分量，yp2为行星轮ⅱ振动位移沿坐标轴y方向的分量，θp2为行星轮ⅱ振动角位移，xzp2为轴承ⅱ沿坐标轴x方向的振动位移，yzp2为轴承ⅱ沿坐标轴y方向的振动位移，xp3为行星轮ⅲ振动位移沿坐标轴x方向的分量，yp3为行星轮ⅲ振动位移沿坐标轴y方向的分量，θp3为行星轮ⅲ振动角位移，xzp3为轴承ⅲ沿坐标轴x方向的振动位移，yzp3为轴承ⅲ沿坐标轴y方向的振动位移，xr为内齿圈振动位移沿坐标轴x方向的分量，yr为内齿圈振动位移沿坐标轴y方向的分量，θr为内齿圈振动角位移；

30、根据动力学模型构建行星齿轮传动系统振动微分方程：

31、太阳轮振动微分方程：

32、

33、其中，ms为太阳轮的质量，ωc为行星轮角位移，xs为太阳轮振动位移沿坐标轴x方向的分量，xp1为行星轮ⅰ振动位移沿坐标轴x方向的分量，xp2为行星轮ⅱ振动位移沿坐标轴x方向的分量，xp3为行星轮ⅲ振动位移沿坐标轴x方向的分量，xzs为太阳轮轴承沿坐标轴x方向的振动位移，为太阳轮沿坐标轴x方向振动位移的二阶导数，为太阳轮沿坐标轴x方向振动位移的一阶导数，为行星轮ⅰ沿坐标轴x方向振动位移的一阶导数，为行星轮ⅱ沿坐标轴x方向振动位移的一阶导数，为行星轮ⅲ沿坐标轴x方向振动位移的一阶导数，为太阳轮轴承沿坐标轴x方向振动位移的一阶导数，ys为太阳轮振动位移沿坐标轴y方向的分量，yp1为行星轮ⅰ振动位移沿坐标轴y方向的分量，yp2为行星轮ⅱ振动位移沿坐标轴y方向的分量，yp3为行星轮ⅲ振动位移沿坐标轴y方向的分量，yzs为太阳轮轴承沿坐标轴y方向的振动位移，为太阳轮沿坐标轴y方向振动位移的二阶导数，为太阳轮沿坐标轴y方向振动位移的一阶导数，为行星轮ⅰ沿坐标轴y方向振动位移的一阶导数，为行星轮ⅱ沿坐标轴y方向振动位移的一阶导数，为行星轮ⅲ沿坐标轴y方向振动位移的一阶导数，为太阳轮轴承沿坐标轴y方向振动位移的一阶导数，为太阳轮与行星轮ⅰ的接触角，为太阳轮与行星轮ⅱ的接触角，为太阳轮与行星轮ⅲ的接触角，为太阳轮振动角位移的二阶导数，fsp1为太阳轮与行星轮ⅰ的啮合力，fsp2为太阳轮与行星轮ⅱ的啮合力，fsp3为太阳轮行星轮ⅲ的啮合力，kzs为太阳轮轴承的支撑刚度，czs为太阳轮轴承的支撑阻尼，g为重力加速度，tin为输入转矩，rs为太阳轮分度圆半径；

34、太阳轮轴承振动微分方程:

35、

36、其中，mzs为太阳轮轴承的质量，为太阳轮轴承沿坐标轴x方向振动位移的二阶导数，为太阳轮轴承沿坐标轴y方向振动位移的二阶导数，kzs为太阳轮0轴承的支撑刚度，czs为太阳轮轴承的支撑阻尼，xzs为太阳轮轴承沿坐标轴x方向的振动位移，xs为太阳轮振动位移沿坐标轴x方向的分量，为太阳轮轴承沿坐标轴x方向振动位移的一阶导数，为太阳轮沿坐标轴x方向振动位移的一阶导数，yzs为太阳轮轴承沿坐标轴y方向的振动位移，ys为太阳轮振动位移沿坐标轴y方向的分量，为太阳轮轴承沿坐标轴y方向振动位移的一阶导数，为太阳轮沿坐标轴y方向振动位移的一阶导数，fzx1为太阳轮轴承沿x方向轴承力的分力，fzy1为太阳轮轴承沿y方向轴承力的分力；

37、行星轮ⅰ振动微分方程:

38、

39、其中，mp1为行星轮ⅰ的质量，ωc为行星轮角位移，xs为太阳轮振动位移沿坐标轴x方向的分量，xp1为行星轮ⅰ振动位移沿坐标轴x方向的分量，xzp1为轴承ⅰ振动位移沿坐标轴x方向的分量，xr为内齿圈振动位移沿坐标轴x方向的分量，为行星轮ⅰ沿坐标轴x方向振动位移的二阶导数，为行星轮ⅰ沿坐标轴x方向振动位移的一阶导数，为轴承ⅰ沿坐标轴x方向振动位移的一阶导数，为内齿圈沿坐标轴x方向振动位移的一阶导数，为太阳轮沿坐标轴x方向振动位移的一阶导数，ys为太阳轮振动位移沿坐标轴y方向的分量，yp1为行星轮ⅰ振动位移沿坐标轴y方向的分量，yzp1为轴承ⅰ振动位移沿坐标轴y方向的分量，yr为内齿圈振动位移沿坐标轴y方向的分量，为行星轮ⅰ沿坐标轴y方向振动位移的二阶导数，为行星轮ⅰ沿坐标轴y方向振动位移的一阶导数，为轴承ⅰ沿坐标轴y方向振动位移的一阶导数，为内齿圈沿坐标轴y方向振动位移的一阶导数，为太阳轮沿坐标轴y方向振动位移的一阶导数，kzp1为轴承ⅰ的支撑刚度，czp1为轴承ⅰ的支撑阻尼，fpr1为行星轮ⅰ与内齿圈的啮合力，为行星轮ⅰ与内齿圈的接触角，fsp1为太阳轮与行星轮ⅰ的啮合力，为太阳轮与行星轮ⅰ的接触角，为行星轮ⅰ振动角位移的二阶导数；

40、轴承ⅰ振动微分方程:

41、

42、其中，mzp1为轴承ⅰ的质量，为轴承ⅰ沿坐标轴x方向振动位移的二阶导数，为轴承ⅰ沿坐标轴y方向振动位移的二阶导数，kzp1为轴承ⅰ的支撑刚度，czp1为轴承ⅰ的支撑阻尼，xp1为行星轮ⅰ沿坐标轴x方向振动位移，xzp1为轴承ⅰ振动位移沿坐标轴x方向的分量，为行星轮ⅰ沿坐标轴x方向振动位移的一阶导数，为轴承ⅰ沿坐标轴x方向振动位移的一阶导数，yp1为行星轮ⅰ沿坐标轴y方向振动位移，yzp1为轴承ⅰ振动位移沿坐标轴y方向的分量，为行星轮ⅰ沿坐标轴y方向振动位移的一阶导数，为轴承ⅰ沿坐标轴y方向振动位移的一阶导数，fzx2为轴承ⅰ沿x方向轴承力的分力，fzy2为轴承ⅰ沿y方向轴承力的分力；

43、行星轮ⅱ振动微分方程:

44、

45、其中，mp2为行星轮ⅱ的质量，ωc为行星轮角位移，xs为太阳轮振动位移沿坐标轴x方向的分量，xp2为行星轮ⅱ振动位移沿坐标轴x方向的分量，xzp2为轴承ⅱ振动位移沿坐标轴x方向的分量，xr为内齿圈振动位移沿坐标轴x方向的分量，为行星轮ⅱ沿坐标轴x方向振动位移的二阶导数，为行星轮ⅱ沿坐标轴x方向振动位移的一阶导数，为轴承ⅱ沿坐标轴x方向振动位移的一阶导数，为内齿圈沿坐标轴x方向振动位移的一阶导数，为太阳轮沿坐标轴x方向振动位移的一阶导数，ys为太阳轮振动位移沿坐标轴y方向的分量，yp2为行星轮ⅱ振动位移沿坐标轴y方向的分量，yzp2为轴承ⅱ振动位移沿坐标轴y方向的分量，yr为内齿圈振动位移沿坐标轴y方向的分量，为行星轮ⅱ沿坐标轴y方向振动位移的二阶导数，为行星轮ⅱ沿坐标轴y方向振动位移的一阶导数，为轴承ⅱ沿坐标轴y方向振动位移的一阶导数，为内齿圈沿坐标轴y方向振动位移的一阶导数，为太阳轮沿坐标轴y方向振动位移的一阶导数，kzp2为轴承ⅱ的支撑刚度，czp2为轴承ⅱ的支撑阻尼，fpr2为行星轮ⅱ与内齿圈的啮合力，为行星轮ⅱ与内齿圈的接触角，fsp2为太阳轮与行星轮ⅱ的啮合力，为太阳轮与行星轮ⅱ的接触角，为行星轮ⅱ振动角位移的二阶导数；

46、轴承ⅱ振动微分方程：

47、

48、其中，mzp2为轴承ⅱ的质量，为轴承ⅱ沿坐标轴x方向振动位移的二阶导数，为轴承ⅱ沿坐标轴y方向振动位移的二阶导数，kzp2为轴承ⅱ的支撑刚度，czp2为轴承ⅱ的支撑阻尼，xp2为行星轮ⅱ沿坐标轴x方向振动位移，xzp2为轴承ⅱ振动位移沿坐标轴x方向的分量，为行星轮ⅱ沿坐标轴x方向振动位移的一阶导数，为轴承ⅱ沿坐标轴x方向振动位移的一阶导数，yp2为行星轮ⅱ沿坐标轴y方向振动位移，yzp2为轴承ⅱ振动位移沿坐标轴y方向的分量，为行星轮ⅱ沿坐标轴y方向振动位移的一阶导数，为轴承ⅱ沿坐标轴y方向振动位移的一阶导数，fzx3为轴承ⅱ沿x方向轴承力的分力，fzy3为轴承ⅱ沿y方向轴承力的分力；

49、行星轮ⅲ振动微分方程：

50、

51、其中，mp3为行星轮ⅲ的质量，ωc为行星轮角位移，xs为太阳轮振动位移沿坐标轴x方向的分量，xp3为行星轮ⅲ振动位移沿坐标轴x方向的分量，xzp3为轴承ⅲ振动位移沿坐标轴x方向的分量，xr为内齿圈振动位移沿坐标轴x方向的分量，为行星轮ⅲ沿坐标轴x方向振动位移的二阶导数，为行星轮ⅲ沿坐标轴x方向振动位移的一阶导数，为轴承ⅲ沿坐标轴x方向振动位移的一阶导数，为内齿圈沿坐标轴x方向振动位移的一阶导数，为太阳轮沿坐标轴x方向振动位移的一阶导数，ys为太阳轮振动位移沿坐标轴y方向的分量，yp3为行星轮ⅲ振动位移沿坐标轴y方向的分量，yzp3为轴承ⅲ振动位移沿坐标轴y方向的分量，yr为内齿圈振动位移沿坐标轴y方向的分量，为行星轮ⅲ沿坐标轴y方向振动位移的二阶导数，为行星轮ⅲ沿坐标轴y方向振动位移的一阶导数，为轴承ⅲ沿坐标轴y方向振动位移的一阶导数，为内齿圈沿坐标轴y方向振动位移的一阶导数，为太阳轮沿坐标轴y方向振动位移的一阶导数，kzp3为轴承ⅲ的支撑刚度，czp3为轴承ⅲ的支撑阻尼，fpr3为行星轮ⅲ与内齿圈的啮合力，为行星轮ⅲ与内齿圈的接触角，fsp3为太阳轮与行星轮ⅲ的啮合力，为太阳轮与行星轮ⅲ的接触角，为行星轮ⅲ振动角位移的二阶导数；

52、轴承ⅲ振动微分方程：

53、

54、其中，mzp3为轴承ⅲ的质量，为轴承ⅲ沿坐标轴x方向振动位移的二阶导数，为轴承ⅲ沿坐标轴y方向振动位移的二阶导数，kzp3为轴承ⅲ的支撑刚度，czp3为轴承ⅲ的支撑阻尼，xp3为行星轮ⅲ沿坐标轴x方向振动位移，xzp3为轴承ⅲ振动位移沿坐标轴x方向的分量，为行星轮ⅲ沿坐标轴x方向振动位移的一阶导数，为轴承ⅲ沿坐标轴x方向振动位移的一阶导数，yp3为行星轮ⅲ沿坐标轴y方向振动位移，yzp3为轴承ⅲ振动位移沿坐标轴y方向的分量，为行星轮ⅲ沿坐标轴y方向振动位移的一阶导数，为轴承ⅲ沿坐标轴y方向振动位移的一阶导数，fzx4为轴承ⅲ沿x方向轴承力的分力，fzy4为轴承ⅲ沿y方向轴承力的分力；

55、内齿圈振动微分方程：

56、

57、其中，mr为内齿圈的质量，ωc为行星轮角位移，xp1为行星轮ⅰ振动位移沿坐标轴x方向的分量，xp2为行星轮ⅱ振动位移沿坐标轴x方向的分量，xp3为行星轮ⅲ振动位移沿坐标轴x方向的分量，xr为内齿圈振动位移沿坐标轴x方向的分量，为内齿圈沿坐标轴x方向振动位移的二阶导数，为行星轮ⅰ沿坐标轴x方向振动位移的一阶导数，为行星轮ⅱ沿坐标轴x方向振动位移的一阶导数，为行星轮ⅲ沿坐标轴x方向振动位移的一阶导数，为内齿圈沿坐标轴x方向振动位移的一阶导数，yp1为行星轮ⅰ振动位移沿坐标轴y方向的分量，yp2为行星轮ⅱ振动位移沿坐标轴y方向的分量，yp3为行星轮ⅲ振动位移沿坐标轴y方向的分量，yr为内齿圈振动位移沿坐标轴y方向的分量，为内齿圈沿坐标轴y方向振动位移的二阶导数，为行星轮ⅰ沿坐标轴y方向振动位移的一阶导数，为行星轮ⅱ沿坐标轴y方向振动位移的一阶导数，为行星轮ⅲ沿坐标轴y方向振动位移的一阶导数，为内齿圈沿坐标轴y方向振动位移的一阶导数，kzp3为轴承ⅲ的支撑刚度，czp3为轴承ⅲ的支撑阻尼，fpr1为行星轮ⅰ与内齿圈的啮合力，fpr2为行星轮ⅱ与内齿圈的啮合力，fpr3为行星轮ⅲ与内齿圈的啮合力，为行星轮ⅰ与内齿圈的接触角，为行星轮ⅱ与内齿圈的接触角，为行星轮ⅲ与内齿圈的接触角，为内齿圈振动角位移的二阶导数，tout为输出转矩，rr为内齿圈分度圆半径；

58、太阳轮无量纲化后振动微分方程：

59、

60、其中，为无量纲行星轮角位移，为太阳轮无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅰ无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅱ无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅲ无量纲振动位移沿坐标轴x方向的分量，为太阳轮轴承沿坐标轴x方向无量纲振动位移的一阶导数，为太阳轮无量纲振动位移沿坐标轴y方向的分量，为行星轮ⅰ无量纲振动位移沿坐标轴y方向的分量，为行星轮ⅱ无量纲振动位移沿坐标轴y方向的分量，为行星轮ⅲ无量纲振动位移沿坐标轴y方向的分量，为太阳轮轴承沿坐标轴y方向无量纲振动位移的一阶导数，为太阳轮沿坐标轴x方向无量纲振动位移的二阶导数，为太阳轮沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅰ沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅱ沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅲ沿坐标轴x方向无量纲振动位移的一阶导数，为太阳轮轴承沿坐标轴x方向无量纲振动位移的一阶导数，为太阳轮沿坐标轴y方向无量纲振动位移的二阶导数，为太阳轮沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅰ沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅱ沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅲ沿坐标轴y方向无量纲振动位移的一阶导数，为太阳轮轴承沿坐标轴y方向无量纲振动位移的一阶导数，为太阳轮振动无量纲角位移的二阶导数，为太阳轮与行星轮ⅰ的无量纲啮合力，为太阳轮与行星轮ⅱ的无量纲啮合力，为太阳轮行星轮ⅲ的无量纲啮合力，κzs为太阳轮轴承的无量纲支撑刚度，ζzs为太阳轮轴承的无量纲支撑阻尼系数，fg为无量纲重力加速度，为太阳轮与行星轮ⅰ的接触角，为太阳轮与行星轮ⅱ的接触角，为太阳轮与行星轮ⅲ的接触角，ωn为固有频率，bm为侧隙的一半，tin为输入转矩，rs为太阳轮分度圆半径；

61、太阳轮轴承无量纲化后振动微分方程:

62、

63、其中，为太阳轮轴承沿坐标轴x方向无量纲振动位移的二阶导数，为太阳轮轴承沿坐标轴y方向无量纲振动位移的二阶导数，κzs为太阳轮轴承的无量纲支撑刚度，ζzs为太阳轮轴承的无量纲支撑阻尼系数，为太阳轮沿坐标轴x方向无量纲振动位移的一阶导数，为太阳轮轴承沿坐标轴x方向无量纲振动位移的一阶导数，为太阳轮沿坐标轴y方向无量纲振动位移的一阶导数，为太阳轮轴承沿坐标轴y方向无量纲振动位移的一阶导数，为太阳轮无量纲振动位移沿坐标轴x方向的分量，为太阳轮轴承沿坐标轴x方向无量纲振动位移的一阶导数，为太阳轮无量纲振动位移沿坐标轴y方向的分量，为太阳轮轴承沿坐标轴y方向无量纲振动位移的一阶导数，为太阳轮轴承沿x方向无量纲轴承力的分力，为太阳轮轴承沿y方向无量纲轴承力的分力；

64、行星轮ⅰ无量纲化后振动微分方程:

65、

66、其中，为无量纲行星轮角位移，为太阳轮无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅰ无量纲振动位移沿坐标轴x方向的分量，为轴承ⅰ无量纲振动位移沿坐标轴x方向的分量，为内齿圈沿坐标轴x方向无量纲振动位移的一阶导数，为太阳轮无量纲振动位移沿坐标轴y方向的分量，为行星轮ⅰ无量纲振动位移沿坐标轴y方向的分量，为行轴承ⅰ无量纲振动位移沿坐标轴y方向的分量，为内齿圈沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅰ沿坐标轴x方向无量纲振动位移的二阶导数，为太阳轮沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅰ沿坐标轴x方向无量纲振动位移的一阶导数，为轴承ⅰ沿坐标轴x方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅰ沿坐标轴y方向无量纲振动位移的二阶导数，为太阳轮沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅰ沿坐标轴y方向无量纲振动位移的一阶导数，为轴承ⅰ沿坐标轴y方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴y方向无量纲振动位移的一阶导数，κzp1为轴承ⅰ的无量纲支撑刚度，ζzp1为轴承ⅰ的无量纲支撑阻尼系数，为行星轮ⅰ与内齿圈的无量纲啮合力，为太阳轮与行星轮ⅰ的无量纲啮合力，为行星轮ⅰ与内齿圈的接触角，为太阳轮与行星轮ⅰ的接触角，fg为无量纲重力加速度，为行星轮ⅰ无量纲振动角位移的二阶导数；

67、轴承ⅰ无量纲化后振动微分方程:

68、

69、其中，为轴承ⅰ沿坐标轴x方向无量纲振动位移的二阶导数，为轴承ⅰ沿坐标轴y方向无量纲振动位移的二阶导数，κzp1为轴承ⅰ的无量纲支撑刚度，ζzp1为轴承ⅰ的无量纲支撑阻尼系数，为行星轮ⅰ沿坐标轴x方向无量纲振动位移的一阶导数，为轴承ⅰ沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅰ沿坐标轴y方向无量纲振动位移的一阶导数，为轴承ⅰ沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅰ无量纲振动位移沿坐标轴x方向的分量，为轴承ⅰ无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅰ无量纲振动位移沿坐标轴y方向的分量，为行轴承ⅰ无量纲振动位移沿坐标轴y方向的分量，为轴承ⅰ沿x方向无量纲轴承力的分力，为轴承ⅰ沿y方向无量纲轴承力的分力；

70、行星轮ⅱ无量纲化后振动微分方程:

71、

72、其中，为无量纲行星轮角位移，为太阳轮无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅱ无量纲振动位移沿坐标轴x方向的分量，为轴承ⅱ无量纲振动位移沿坐标轴x方向的分量，为内齿圈沿坐标轴x方向无量纲振动位移的一阶导数，为太阳轮无量纲振动位移沿坐标轴y方向的分量，为行星轮ⅱ无量纲振动位移沿坐标轴y方向的分量，为行轴承ⅱ无量纲振动位移沿坐标轴y方向的分量，为内齿圈沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅱ沿坐标轴x方向无量纲振动位移的二阶导数，为太阳轮沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅱ沿坐标轴x方向无量纲振动位移的一阶导数，为轴承ⅱ沿坐标轴x方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅱ沿坐标轴y方向无量纲振动位移的二阶导数，为太阳轮沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅱ沿坐标轴y方向无量纲振动位移的一阶导数，为轴承ⅱ沿坐标轴y方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴y方向无量纲振动位移的一阶导数，κzp2为轴承ⅱ的无量纲支撑刚度，κzp2为轴承ⅱ的无量纲支撑阻尼系数，为行星轮ⅱ与内齿圈的无量纲啮合力，为太阳轮与行星轮ⅱ的无量纲啮合力，为行星轮ⅱ与内齿圈的接触角，为太阳轮与行星轮ⅱ的接触角，fg为无量纲重力加速度，为行星轮ⅱ无量纲振动角位移的二阶导数；

73、轴承ⅱ无量纲化后振动微分方程：

74、

75、其中，为轴承ⅱ沿坐标轴x方向无量纲振动位移的二阶导数，为轴承ⅱ沿坐标轴y方向无量纲振动位移的二阶导数，κzp2为轴承ⅱ的无量纲支撑刚度，ζzp2为轴承ⅱ的无量纲支撑阻尼系数，为行星轮ⅱ沿坐标轴x方向无量纲振动位移的一阶导数，为轴承ⅱ沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅱ沿坐标轴y方向无量纲振动位移的一阶导数，为轴承ⅱ沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅱ无量纲振动位移沿坐标轴x方向的分量，为轴承ⅱ无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅱ无量纲振动位移沿坐标轴y方向的分量，为行轴承ⅱ无量纲振动位移沿坐标轴y方向的分量，为轴承ⅱ沿x方向无量纲轴承力的分力，为轴承ⅱ沿y方向无量纲轴承力的分力；

76、行星轮ⅲ无量纲化后振动微分方程：

77、

78、其中，为无量纲行星轮角位移，为太阳轮无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅲ无量纲振动位移沿坐标轴x方向的分量，为轴承ⅲ无量纲振动位移沿坐标轴x方向的分量，为内齿圈沿坐标轴x方向无量纲振动位移的一阶导数，为太阳轮无量纲振动位移沿坐标轴y方向的分量，为行星轮ⅲ无量纲振动位移沿坐标轴y方向的分量，为行轴承ⅲ无量纲振动位移沿坐标轴y方向的分量，为内齿圈沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅲ沿坐标轴x方向无量纲振动位移的二阶导数，为太阳轮沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅲ沿坐标轴x方向无量纲振动位移的一阶导数，为轴承ⅲ沿坐标轴x方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅲ沿坐标轴y方向无量纲振动位移的二阶导数，为太阳轮沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅲ沿坐标轴y方向无量纲振动位移的一阶导数，为轴承ⅲ沿坐标轴y方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴y方向无量纲振动位移的一阶导数，κzp3为轴承ⅲ的无量纲支撑刚度，ζzp3为轴承ⅲ的无量纲支撑阻尼系数，为行星轮ⅲ与内齿圈的无量纲啮合力，为太阳轮与行星轮ⅲ的无量纲啮合力，为行星轮ⅲ与内齿圈的接触角，为太阳轮与行星轮ⅲ的接触角，fg为无量纲重力加速度，为行星轮ⅲ无量纲振动角位移的二阶导数；

79、轴承ⅲ无量纲化后振动微分方程：

80、

81、其中，为轴承ⅲ沿坐标轴x方向无量纲振动位移的二阶导数，为轴承ⅲ沿坐标轴y方向无量纲振动位移的二阶导数，κzp3为轴承ⅲ的无量纲支撑刚度，ζzp3为轴承ⅲ的无量纲支撑阻尼系数，为行星轮ⅲ沿坐标轴x方向无量纲振动位移的一阶导数，为轴承ⅲ沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅲ沿坐标轴y方向无量纲振动位移的一阶导数，为轴承ⅲ沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅲ无量纲振动位移沿坐标轴x方向的分量，为轴承ⅲ无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅲ无量纲振动位移沿坐标轴y方向的分量，为行轴承ⅲ无量纲振动位移沿坐标轴y方向的分量，为轴承ⅲ沿x方向无量纲轴承力的分力，为轴承ⅲ沿y方向无量纲轴承力的分力；

82、内齿圈无量纲化后振动微分方程：

83、

84、其中，为无量纲行星轮角位移，为行星轮ⅰ无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅱ无量纲振动位移沿坐标轴x方向的分量，为行星轮ⅲ无量纲振动位移沿坐标轴x方向的分量，为内齿圈沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅰ无量纲振动位移沿坐标轴y方向的分量，为行星轮ⅱ无量纲振动位移沿坐标轴y方向的分量，为行星轮ⅲ无量纲振动位移沿坐标轴y方向的分量，为内齿圈沿坐标轴y方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴x方向无量纲振动位移的二阶导数，为行星轮ⅰ沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅱ沿坐标轴x方向无量纲振动位移的一阶导数，为行星轮ⅲ沿坐标轴x方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴x方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴y方向无量纲振动位移的二阶导数，为行星轮ⅰ沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅱ沿坐标轴y方向无量纲振动位移的一阶导数，为行星轮ⅲ沿坐标轴y方向无量纲振动位移的一阶导数，为内齿圈沿坐标轴y方向无量纲振动位移的一阶导数，κzp3为轴承ⅲ的无量纲支撑刚度，ζzp3为轴承ⅲ的无量纲支撑阻尼系数，为行星轮ⅰ与内齿圈的无量纲啮合力，为行星轮ⅱ与内齿圈的无量纲啮合力，为行星轮ⅲ与内齿圈的无量纲啮合力，为行星轮ⅰ与内齿圈的接触角，为行星轮ⅱ与内齿圈的接触角，为行星轮ⅲ与内齿圈的接触角，为内齿圈无量纲振动角位移的二阶导数，rr为内齿圈分度圆半径，fg为无量纲重力加速度，bm为侧隙的一半，ωn为固有频率，tout为输出转矩，mr为内齿圈的质量；

85、通过数值方法求解无量纲化后系统振动微分方程，可得到初始条件下系统动力学响应，采用胞映射法将振动系统转化为胞映射系统，将行星齿轮传动系统的相空间等分为海量的胞，将每个胞视为一个整体，胞的中心点特征代表胞特征，以初始条件下系统的动力学响应为初值，反复使用胞映射，记录胞中心的变迁过程，通过对比激励频率与齿轮裂纹下行星齿轮传动系统全局响应，探究齿轮裂纹对系统全局非线性动力学的影响机理，并对系统参数进行优化。

86、与现有技术相比，本发明的有益效果：该方法构建了行星齿轮传动系统全局非线性损伤动力学模型，提高传统行星齿轮传动系统动力学模型的精确性，为行星齿轮传动系统设计、优化与寿命预测提供了强力支撑，既填补含裂纹的行星齿轮传动系统动力学领域相关技术空白，又可产生较大的社会效益与经济效益。