一种基-2低延迟蒙哥马利模乘ASIC模块及其方法

本发明涉及一种基-2低延迟蒙哥马利模乘asic模块及其方法，属于超大规模集成电路的信息加密领域。

背景技术：

1、蒙哥马利算法(montgomery algorithm)是一种用于高效执行大整数模乘和模幂运算的优化算法，使用比较简单的加法乘法与移位即可实现模乘的算法。它在密码学和计算机科学领域中被广泛应用，特别是在rsa公钥加密算法和椭圆曲线密码算法中作为密码系统研究的焦点。

2、蒙哥马利模乘是一种用于加密算法中的模运算方法，它可以加速大数的模运算。具体的运算过程如下：

3、首先，选择一个模数n和一个基数r(r＝2k)，使得n和r互质(即它们的最大公约数为1)；

4、将要进行模乘的两个数a和b转换为蒙哥马利形式，其中a，b满足2k-1≤a，b≤2k。蒙哥马利形式是指将数x转换为x’，使得x’≡xr(mod n)；

5、对转换后的数进行模乘运算：s’＝a’×b’(mod n)；

6、最后，将得到的结果s’转换回蒙哥马利模乘常规形式s，使得s≡s’r(mod n)。

7、蒙哥马利模乘算法的主要思想是将模乘运算转换为一系列移位、加法和减法操作，以减少乘法和模运算的次数，从而提高计算效率。该算法通过预处理输入数据，将模乘运算转化为一系列快速的位运算，从而加速了模乘的计算过程。蒙哥马利模乘的优点在于它可以通过转换为蒙哥马利形式来减少模运算的次数，从而提高计算效率。蒙哥马利模乘算法的优点包括高效性和安全性，使其成为许多加密算法中的重要组成部分。它在实际应用中能够显著提高加密操作的速度，同时保持较高的安全性。

8、蒙哥马利模乘算法的主要缺陷是实现复杂性，需要对输入数据进行预处理和转换，以及精确的位运算和模运算。同时蒙哥马利模乘算法在资源浪费和时间延迟方面存在一些缺陷。首先，由于该算法的实现相对复杂，需要进行预处理和转换，以及精确的位运算和模运算，因此可能导致资源的浪费，例如额外的存储空间和计算资源的占用。其次，对输入数据的限制也会导致额外的处理步骤，从而增加了计算的时间延迟。

9、随着技术的发展和ic设计规模的扩大，一个庞大的系统设计会由多个团队共同完成，这时就需要把一个系统合理划分为多个模块，从而充分利用人力资源，同时也利于系统的调试与逻辑综合。因此，在实际应用中，需要更加适合硬件实现的方案对上述操作进行替代。

技术实现思路

1、本发明的目的在于优化电路硬件面积，降低蒙哥马利模乘算法在运算过程中的延迟，减少资源消耗的同时提高运算速度，从而提供一种基-2低延迟蒙哥马利模乘算法asic模块及其方法。

2、本发明模块采用的技术方案如下：

3、一种基-2低延迟蒙哥马利模乘asic模块，包括：

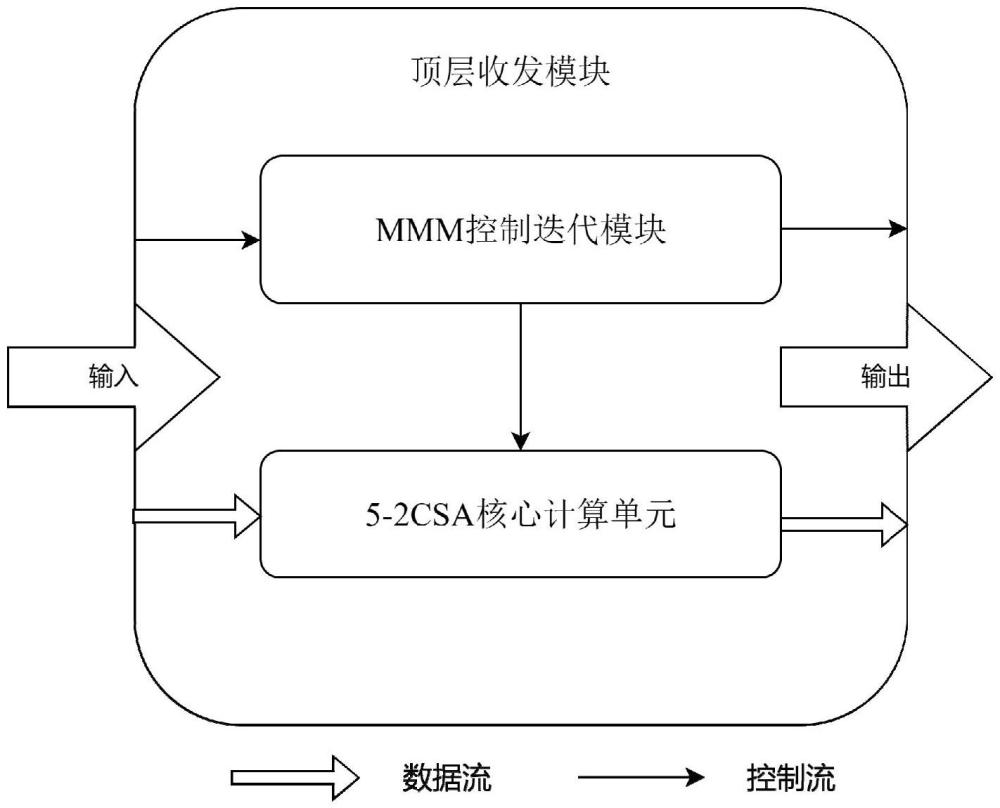
4、顶层收发模块，用于获取第一输入变量a、第二输入变量b、模数n以及来自5-2csa核心计算单元模块的中间结果s’，并控制mmm控制迭代模块及5-2csa核心计算单元模块进行计算，得到蒙哥马利模乘结果s；

5、5-2csa核心计算单元模块，用于接受顶层收发模块传输的第一输入变量a、第二输入变量b以及模数n，进行蒙哥马利模乘计算，并将得到的中间结果s’传输回顶层收发模块中；

6、mmm控制迭代模块，用于控制5-2csa核心计算单元模块的蒙哥马利模乘计算的迭代过程。

7、本发明还提供一种基-2低延迟蒙哥马利模乘asic模块的方法，该方法具体步骤包括：

8、(1)当顶层收发模块接受到第一输入变量a、第二输入变量b和模数n时，根据输入变量的位长k得到r＝22k mod n，随后将变量a和r传入5-2csa核心计算单元模块中；

9、(2)将传入5-2csa核心计算单元模块内的两个变量分别记作x和y，并将第二变量y的位长扩展一位为k+1位后左移一位，令y的最低位y[0]＝0，然后计算第一变量x的第0位与第二变量y的进位保留格式y1、y2相乘；同时从两个寄存器s1、s2中读取数值，计算两个寄存器中的第0位与模数n相乘，并将结果与s1、s2中的数值共同进行三次保留进位加法操作，计算结果保存在寄存器s1、s2中；

10、(3)将步骤(2)中的过程重复k次，每次计算过程中将第一变量x的第0位替换为x的第i位，并在运算结束后将i自增1，当i的值等于k时标志完成k+1次循环，终止迭代运算；最终将s1、s2中的数值相加得到最终结果作为中间结果作为a’输出，a’为变量a在n范围内的蒙哥马利形式；

11、(4)将第二输入变量b和r传入5-2csa核心计算单元模块中，并重复步骤(2)和(3)，获得b’输出，b’为变量b在n范围内的蒙哥马利形式。

12、(5)将蒙哥马利形式a’和b’传入5-2csa核心计算单元模块中，并重复步骤(2)和(3)，获得s’输出，s’为第一输入变量a与第二输入变量b以n为模数模乘的最终结果s在n范围内的蒙哥马利形式；

13、(6)将s’和1传入5-2csa核心计算单元模块中，并重复步骤(2)和(3)，获得s输出，s即为蒙哥马利模乘最终结果。

14、本发明具有以下有益效果：

15、(1)本发明对蒙哥马利模乘算法的实现方式进行了结构性的调整与优化，极大地降低了蒙哥马利模乘计算过程中的延迟问题。

16、(2)本发明采用了一种高效低延迟模乘方式，通过将输入变量b左移一位，优化了对于中间变量q的运算，在减少了一次加法和一次高位乘法运算的同时，算法单次迭代用时减半，减少复杂度的同时缩减了系统整体延时。

17、(3)本发明在基-2蒙哥马利模乘乘法器中，引入了进位保留加法器(csa)，在计算所有位的结果过程中保留进位信号，同时为避免大位宽加法中的长进位链问题，引入三级csa结构组成5-2csa核心计算单元进行计算，保障电路的稳定性的同时增加操作数，降低关键延时。

18、(4)提出了一种新型的应用于专用集成电路asic模块，对其进行模块式划分，能提高设计的复用性和可维护性，降低设计复杂度。

技术特征：

1.一种基-2低延迟蒙哥马利模乘asic模块，其特征在于，该模块包括：

2.根据权利要求1所述的一种基-2低延迟蒙哥马利模乘asic模块，其特征在于，所述的5-2csa核心计算单元模块具有5个输入及两个输出，包括两个乘法器、两个全加器、两个寄存器、一个旁路计算通路及三级csa进位保留加法器。

3.根据权利要求1所述的一种基-2低延迟蒙哥马利模乘asic模块，其特征在于，所述顶层收发模块为包括四个状态的状态机结构，四个状态分别为：将第一输入变量a转化为蒙哥马利形式a’、将第二输入变量b转化为蒙哥马利形式b’、在蒙哥马利域中进行计算和最终转化为模乘结果s。

4.根据权利要求1所述的一种基-2低延迟蒙哥马利模乘asic模块，其特征在于，所述mmm控制迭代模块包括四个状态的状态机结构，四个状态分别为：复位状态reset、循环状态loop、完成状态final和输出状态out。

5.利用如权利要求1所述一种基-2低延迟蒙哥马利模乘asic模块的方法，其特征在于，该方法具体步骤包括：

6.根据权利要求5所述的方法，其特征在于，所述步骤(2)中，5-2csa核心计算单元模块包括三级csa进位保留加法器，将s的运算转化为保留进位格式，即

7.根据权利要求6所述的方法，其特征在于，所述5-2csa核心计算单元模块的具体计算步骤包括：对于输入的a1、a2、b1、b2及模数n，其中a1、a2、b1、b2分别为变量a、b的进位保留格式，先对a1、a2进行全加后得到结果的第i位分别与b1、b2进行相乘，得到a[i]b1及a[i]b2；随后计算n’＝(s10^s20)×n；然后将前三个操作数s1、s2和a[i]b1作为第一级csa进位保留加法器的输入在第一个时钟周期参与运算，得到的结果与第四个操作数a[i]b2作为第二级csa进位保留加法器的输入在第二个时钟周期参与运算，再将得到的结果与第五个操作数作为第三级csa进位保留加法器的输入在第三个时钟周期参与运算，得到最终的和sum以及进位carry，即s1与s2；最后将s1和s2全加得到最终结果s并输出；其中第五个操作数是先由s10与s20异或后的结果与模数n相乘后的结果。

8.根据权利要求5所述的方法，其特征在于，所述mmm控制迭代模块根据5-2csa核心计算单元模块输出计算结果s’与控制迭代模块运行状态选择目前需要进行的状态，具体状态转换过程为：当状态为复位状态reset时，将各个输出信号及计数器置0；等待启动使能信号en置于高位时，则进入循环状态loop，在使5-2csa核心计算单元模块运行的同时，计数器自增1，如果计数器未达到位数k-1，则在下个时钟信号到来前保持循环状态，否则进入计算完成状态final，随后输出完成信号done，并进入输出状态out；在输出状态时，表示已经完成一次蒙哥马利模乘，将结果输出给顶层收发模块的同时，保持输出状态，直到收到复位信号reset＝1，进入复位状态，准备进入下次模乘运算。

技术总结本发明提供了一种基‑2低延迟蒙哥马利模乘ASIC模块及其方法。其模块包括：顶层收发模块，用于获取第一输入变量A、第二输入变量B、模数N以及来自5‑2CSA核心计算单元模块的中间结果S’，并控制MMM控制迭代模块及5‑2CSA核心计算单元模块进行计算，得到蒙哥马利模乘结果S；5‑2CSA核心计算单元模块，用于接受顶层收发模块传输的第一输入变量A、第二输入变量B以及模数N，进行蒙哥马利模乘计算，并将得到的中间结果S’传输回顶层收发模块中；MMM控制迭代模块，用于控制5‑2CSA核心计算单元模块的蒙哥马利模乘计算的迭代过程。本发明优化了电路模块的面积开销，使实际运行中所需的时延和资源大大减少。技术研发人员：王宇宣,詹远志,崔展豪,梅正宇,彭成磊,潘红兵受保护的技术使用者：南京大学技术研发日：技术公布日：2024/8/27