一种海底反射条件下的水下航行器吸声材料拓扑优化方法

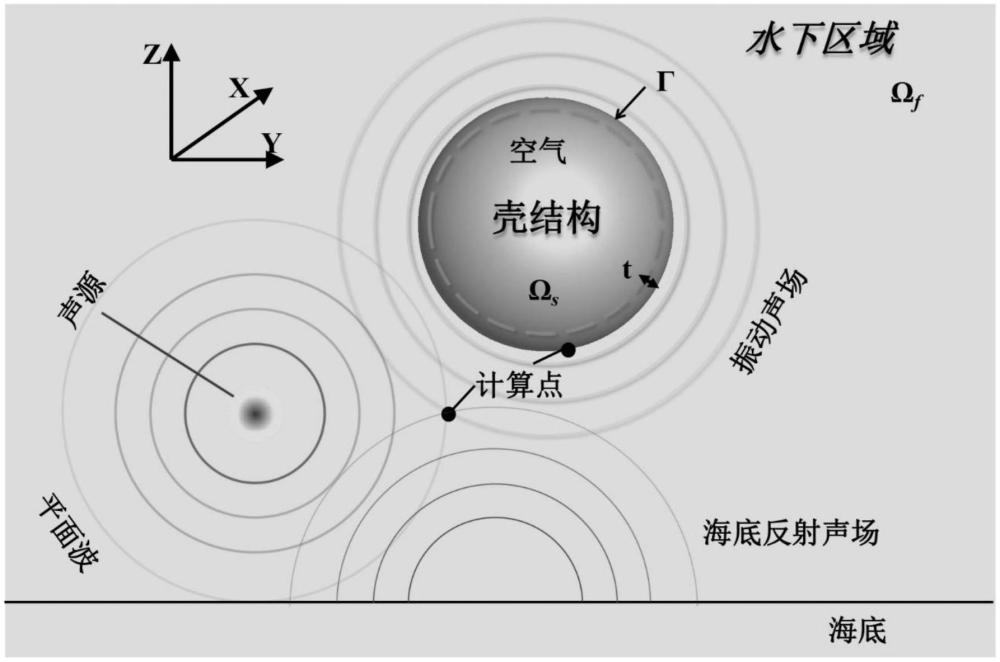
本发明涉及一种在海底反射条件下的水下航行器吸声材料拓扑优化方法，属于声学计算与结构优化领域。

背景技术：

1、

2、传统的材料分布设计方法主要依靠工程经验和反复试错，效率低下。拓扑优化方法结合了声学仿真(如边界元法)和约束优化算法，可以自动寻找最优的拓扑构形或材料布局，是结构设计领域的研究热点。目前已涌现出以变密度法、渐进结构优化和水平集优化等为代表的一系列拓扑优化方法。其中变密度法提出较早，计算效率高，适用于各种不规则结构，是现今应用最为广泛，商业软件开发最为成熟的算法之一。

3、在现实场景中，海底反射会严重干涉目标振动声场，大幅增加声学数值计算与拓扑优化的复杂度。此外，在水声场问题中，声波多在宽频范围内分布，同时考虑到传统声学边界元的矩阵为非对称系数满阵，计算成本和存储成本往往难以承受。尤为重要的是，在传统拓扑优化方法中，复杂结构的cad模型到cae模型的转化是一个非常繁琐的过程，网格划分消耗了大量人力和时间，优化以后的模型也需要后处理才可以导入cad系统，这严重制约了优化过程的自动化程度，难以满足产品快速研发的需求。

技术实现思路

1、有鉴于现有技术的上述缺陷，本发明旨在提供一种高效的水下航行器吸声材料拓扑优化方法。技术方案如下：

2、st1、准备计算数据，获取计算相关参数，使用非均匀有理b样条(nurbs)建构三维几何模型。

3、st2、构建海底反射条件下的水下航行器声学等几何边界元方程，并采用宽频快速多极方法进行加速，计算目标物体表面和相邻区域的声场分布。

4、st3、基于变密度法建立拓扑优化模型，使用伴随变量法和等几何边界元求解敏感度，对结构表面的吸声材料分布进行拓扑优化。

5、st4、计算结果后处理，得到目标表面和周围区域的声场分布图，再给出优化后的声场分布图，以及吸声材料分布的拓扑优化建议。

6、st5、树状计算结构，使用该结构明确计算流程，联结前四步，实现低频和高频计算的转换以及连续优化。

7、所述步骤st1包括：

8、st1.1、首先明确计算参数，包括：入射波频率ω，外部液体密度ρf，目标物体密度ρs，物体几何尺寸，杨氏模量e，泊松比μ，物体壳厚度t。假设存在区域ωf，边界补集ωc＝u\ωf，u表示全集。本问题为外声场问题，分析域ωf为有限域，补集ωc为无限域。假设ωf内充满均匀的理想流体介质，则声压满足波动方程：

9、

10、式中，表示拉普拉斯算子，p(x,t)为时刻t声场ωf中点x处的声压，cf表示波速，d表示维数，可取2或3，分别代表二维或三维问题。

11、st1.2、使用三维建模软件(如rhino3d)构建三维结构的nurbs几何模型。

12、所述步骤st2包括：

13、st2.1、构建海底反射条件下的声学边界积分方程，主要公式如下：

14、静态线性声场中的helmholtz方程边界积分形式为

15、

16、上式中，γ是结构边界；如果源点x周围边界γ光滑，相关系数c(x)为p(x)是声压，pi(x)是事件波，q(y)和q*(x,y)是p(y)和p*(x,y)的常微分，y是域内点，p*(x,y)是基本解。是计算柯西主值的积分。对于3d全空间声波问题，p*(x,y)的值为其中k是波数，r＝|y-x|。在半空间问题中，用表示基本解，表达式为

17、

18、其中x是x关于无限平面γh的镜像，β是海底反射系数，固体平面取1，软平面取-1。对于半空间散射问题，如果事件波与平面不平行，亥姆霍兹方程中的pi(x)应该包含无限平面的反射波。

19、考虑γ上的边界条件：

20、

21、

22、p(x)＝zv(x),onγz,

23、其中，i是虚拟单元，p是介质密度，ω是角频率，v(x)是法向速度，z是声阻抗。带上横线的量是给定边界值。

24、将helmholtz边界积分方程记为cbie，使用burton-miller方法解决cbie在本征频率处有非唯一解的问题。burton-miller方程的微分形式为：

25、

26、其中，α是耦合常数，这里为符号为发散积分的hadamard有限部分，且有

27、

28、st2.2、利用nubrs基函数离散声学边界积分方程，主要公式如下：

29、把声学边界积分方程中的区域边界γ离散为ne个不重叠的nurbs单元，可得：

30、

31、其中，对于cbie有

32、

33、

34、或者对于burton-miller方程有

35、

36、

37、以上方程中，γj表示单元j，在所有边界点处计算并表示为矩阵形式，可得：

38、hp＝gq,

39、引入边界条件，上式可改写为以下形式：

40、aψ＝bφ,

41、其中ψ和φ分别为未知和已知向量。a和b为系数矩阵。所有边界条件已给出，现在该方程已可以求解。

42、st2.3、使用宽频法扩展快速多极算法的应用范围，以解决快速多极边界中低频和高频方法不兼容的问题。在低频区，扩充全空间基本解为以下形式：

43、

44、其中，o是靠近y的展开点，和分别为

45、

46、

47、其中，是的共轭复数，jn和hn分别为一类n阶球形bessel和hankel方程，是球谐函数且

48、

49、其中，表示相关的legendre函数；r，θ和φ表示向量a的球坐标。

50、全空间基本解的平面波展开方程可以写为

51、

52、这里，x'是x附近的展开点(如图3所示)，在单位球s上进行积分，k表示s上指向外部的单位向量，t为对角平移函数且有

53、

54、其中，a＝|a|,a＝a/a，pn是legendre多项式。

55、下面扩展快速多极边界元使其适合半空间问题，首先调整半空间基本解至以下形式：

56、

57、再重写hij和gij的表达式得到

58、

59、

60、然后根据全空间基本解方程，在远离源点x的边界单元γj应用边界积分，具体如下：

61、

62、以及

63、

64、其中，yj是γj上的域点；和分别是低频和高频fmm在实数域的多极矩，具体形式为

65、

66、以及

67、

68、接近o的边界单元组的多极矩，所有在相同叶空间且集中在o的单元，均能相加组成叶空间的矩，即

69、

70、

71、在低频fmm方法中，如果根据m2m(矩到矩)变换方程，矩中心可以从o转换为o'，即

72、

73、这里，wn,n',m,m',l为

74、

75、其中，为wigner的3j符号，集合l为

76、l(n,n',m,m')＝{l|l∈z,n+n'-l:even,max{|m+m'|,|n-n'|}≤l≤n+n'}.在m2l(矩到局部展开系数)转换方程中，考虑了无限或对称平面的影响，表达式为：

77、

78、然后，使用l2l(局部展开到局部展开)转换方程，局部展开中心可以从x'转换至x”，表达式为

79、

80、

81、

82、最后，对于接近o并且原理源点x的边界单元组，或可以使用局部展开系数在低频fmm以展开式的形式表达为

83、或

84、在高频快速多极算法中，表达式为：

85、或

86、在宽频快速多极算法中，m2f方程被用来将低频矩转换为高频矩，表达式为

87、

88、使用以下形式的h2l方程，高频快速多极算法的局部展开系数可以被转换为低频快速多极算法中的形式，表达式为

89、

90、最后，burton-miller方程的转换系数为：

91、或

92、或

93、所述步骤st3包括：

94、st3.1、首先，采用delany-bazley-mikiji经验公式对吸声材料进行插值，具体形式为

95、

96、

97、其中，表示吸声材料的声抗阻率，为无量纲值，ρc为平面波对应的声抗阻值。为复数波，σ为流阻，单位为n·s/m4，f为频率。其中，铺设单层多孔吸声材料结构表面的声阻抗可以根据阻抗传递定理计算，具体为

98、

99、其中，z为多孔吸声材料承受入射波表面的声阻抗，即整体多孔结构表面的声阻抗，为多孔吸声材料的声阻抗，zs为未布置吸声材料结构表面的声阻抗值，d为多孔吸声材料的厚度。

100、当假设结构为刚性结构时，zs＝∞，则上式可以化简为：

101、

102、根据该声阻抗值，多孔结构的反射系数r和吸声系数αs分别为：

103、

104、αs＝1-|r|2.

105、st3.2、接着，使用导纳形式将材料模型引入到声学边界元求解中。首先，导纳边界条件为：

106、q(x)＝ikβ(x)p(x),

107、其中，β(x)＝ρc/z(x)为归一化导纳值，将上式离散后代入边界元系统方程中，可以得到：

108、(h-gy)p＝pi,

109、式中，h和g为边界元系数矩阵，pi为入射波对应的列向量。y是块状对角矩阵，使用常单元离散边界，该矩阵变为对角矩阵，可以表示为

110、

111、其中，βe表示第e个单元的归一化导纳值。考虑导纳边界条件，计算域内点处声压值的系统方程可同样写为

112、

113、式中，pf为域内点对应的声压列向量，hf和gf为场点x位于域内时对应的系数矩阵，为入射波在域内点处的声压列向量。

114、st3.3、最后，针对材料边界元公式，以目标物体表面的声压作为优化目标。将目标函数π表示为结构边界声压p和域内点处声压pf的实函数，则结构表面的吸声材料拓扑优化问题的数学模型可表示为

115、

116、s.t.g(u)-g0≤0,

117、(h-gb)p-pin＝0,

118、

119、0≤μmin≤μe≤1,e＝1,...,nd,

120、其中，为设计变量的列向量，其元素值为实数，nd为设计变量的个数。μe＝0表示该单元表面没有被吸声材料覆盖，μe＝1则表示表面敷设有吸声材料。约束条件包含四个，第一个表示为设计变量的函数，第二个和第三个分别为边界积分方程和域内积分方程的离散形式，第四个为设计变量的上下限。

121、利用变密度拓扑优化方法(simp)方法将导纳值插值为设计变量μe的函数，有

122、

123、其中，βe表示单元e表面归一化导纳值，β0表示单元表面覆盖有吸声材料时的归一化导纳值。η为惩罚因子，目的是使中间密度值向0和1逼近，从而获得边界清晰的拓扑分布。当吸声材料敷设在刚性壁面上时，β0可以表示为

124、

125、式中，可以根据delany-bazley-miki阻抗模型计算得到。

126、下面将给出基于伴随变量法的灵敏度推导过程。首先，将目标函数对任一设计变量μe的导数值拆分为三部分，如下式所示：

127、

128、其中，z1、z2和z3同样为辅助变量，可根据链式微分法则和目标函数的具体形式推导得出，z3不含任何状态变量对设计变量的导数值，即不含和为了保证计算效率，使用伴随变量法直接计算目标函数对设计变量的导数值。为此，将边界积分方程和域内积分方程的离散形式代入目标函数中，得到新的目标函数具体表达式为

129、

130、其中，和为任意选取的伴随变量，其大小分别等于边界上的自由度数和域内计算点的数目。对上式进行微分运算，可以得到

131、

132、其中，系数矩阵h和g只受分析边界γ和频率影响，而hf和gf则只受分析边界γ、域内点位置和频率影响。假设优化过程中，分析边界γ、域内点位置和频率都不会发生变化，则这些系数矩阵的导数项可以直接舍去。此外假设外激励在优化过程中同样保持不变，则有和因此，上式可以简化为

133、

134、对上式进行重组且代入公式中，可以得到

135、

136、由于伴随向量和可以任意选择，让它们满足伴随方程：

137、

138、这里，有根据可以使用广义最小残差法(gmres)求解器联合伴随状态下的快速算法快速求解出求解得到伴随变量和后，目标函数对任意设计变量μe的导数可根据的公式表示为

139、

140、其中，和都可以使用伴随状态下的快速算法进行加速计算得到。

141、最后，以获得域内声压最小值为目标，目标函数可表示为

142、

143、其中，上标表示共轭转置。根据目标函数的具体形式和公式可以得到辅助变量和z3为

144、

145、在推导上式过程中使用了到以下关系：

146、

147、st4、使用绘图工具，将st2中的声压分布绘制成云图，同时将优化后的声压分布绘制成图，并给出优化后的吸声材料拓扑分布，即可实现声压预测以及相应的吸声材料优化。

148、st5、使用树结构实现循环计算和优化，其中，m为低频多极矩，f为低频向高频转换的方程，h为高频多极矩，l为局部展开。两符号之间的“2”代表“转换”，例如m2m表示由低频矩到高频矩的转换。

149、计算时，假设一个包含γ的立方体为0级空间。将该空间(父空间)分为八个相同的1级子空间(内部含边界单元)。不断将空间细分直到其中单元数小于指定值，将最后的(最低级)空间称为叶空间。现做出如下定义，相同等级的空间如果拥有至少一个共同顶点，则称其为“相邻”，如果两个空间不相邻但其父空间相邻，则称其为“完全分离”。空间c中全部“完全分离”的空间集合组成c的交互集合。与c空间的父空间不相邻的空间称为c空间的“远空间”。在高-低频快速多极算法间的转换等级s需满足ds+1＜d且ds≥d(ds和ds+1为s和s+1级空间的尺寸，d是高-低频快速多极算法的阈值)。

150、计算过程主要分为向上传递和向下传递。向上传递时，计算2级以下空间的多极矩。对于l级叶空间c，多极矩是包含从c到c中心的所有边界单元的和。如果l＞s，使用低频矩，否则使用高频矩。对于l级非叶空间c，如果l≥s，使用m2m转换将多极矩从其子空间的中心转换至其中心，如果l＜s，则使用f2f转换。然后对所有转换后的矩求和来获得空间c的多极矩。对于l＝s，在m2m转换之后需要使用m2f转换来将低频矩转换为高频矩。

151、向下传递时，对于l≥2级空间计算其局部展开系数，l级空间c的局部展开系数包含两部分：一个使用m2l转换(l＞s)或f2h转换(l≤s)，通过在c的交互集合中的全部空间获得；另一个使用l2l转换(l＞s)或h2h转换(l≤s)，通过c的远空间获得。对于任意2级空间，系数仅通过m2l或f2h转换获得。在向下传递过程中，当l＝s，需要使用h2l转换来将高频快速多极算法的局部展开系数转换为对应低频快速多极算法转换系数。

152、本发明的有益效果：

153、本发明提出了一种海底反射条件下的水下航行器吸声材料拓扑优化方法。本方法的优势在于，整合了cad与cae，无需划分网格，可以快速计算受海底反射影响的水下航行器振动声场以及敏感度，自动搜寻最优的吸声材料拓扑分布，且优化模型可以直接导入cad系统，从而为水下航行器的优化设计提供指导。