一种自扩散式平面扩散系数测量方法

本发明涉及一种扩散系数测量方法，具体涉及一种自扩散式平面扩散系数测量方法。

背景技术：

1、扩散现象是指物质分子从高浓度区域向低浓度区域转移直到均匀分布的现象。扩散现象是基于分子热运动的输运现象，是趋向于热平衡态的驰豫过程，是熵驱动的过程。从微观角度上看，粒子无规则热运动将会引起扩散，而从宏观角度，浓度梯度的存在造成了扩散。随着时间的进行，扩散系统中浓度梯度会逐渐变小，直至消失。扩散现象广泛存在于三相态中，不仅是同种态之间会存在扩散现象，不同态之间也存在扩散现象，甚至同种物质的不同浓度之间都会发生扩散现象。扩散现象表明，一切物质的分子都在不停地做无规则的运动。扩散现象广泛应用于物理、化工、生物及医学等领域中，在生活中也较为常见，但其微观机制却较为复杂，特别是液体体系中的扩散。由于液体粒子间的相互作用十分复杂，液体运动学说远远没有气体运动学说那样深入，使得对液体扩散理论的处理远比气体或固体困难。

2、扩散系数是从宏观的角度描述扩散程度的物理量。对扩散系数的测量为研究物质扩散的微观机制提供了重要的实验手段，因而扩散系数是科学工作者研究的重中之重。液相扩散系数是溶液粘度与纯溶剂粘度的比值，是研究传质过程，计算传质速率及化工设计与开发的重要基础数据。目前对于液相分子扩散系数的测定还不是很准确；因此，进行对液相分子扩散系数测定的研究很有实用价值，能够很好地解决液相分子扩散系数研究缺乏的问题。

3、传统的测量液相扩散系数的方法包括膜池法、全息干涉法、泰勒分散法、毛细管法等。其中，膜池法所需操作时间长，全息干涉法测量精度高但对实验装置的稳定性要求高，泰勒分散法由于设备加工精度的限制导致其测量精度较低，而且传统的对液体扩散系数的测定多为重力场下的扩散情形。

4、近年来，anand等研究者发明了数字全息干涉法测量液相扩散系数，该方法用ccd相机作为探测器，与计算机相连，实时记录干涉条纹，通过其携带的浓度信息解出扩散系数。该测量方法有着较高的液相扩散系数测量精确度，但其抗环境干扰能力不强，易出现由于装置不稳导致干涉条纹模糊造成较大的误差的情况，对所需要的实验环境和实验条件要求较为严格；国内也有较多关于测定液体扩散系数装置的相关研究，天津大学的张建侯、袁继堂等研究者针对膜池法的主要缺点，选用了金属扩散膜代替传统的玻璃膜，扩散池由池体、扩散膜、池塞及搅拌棒组成，金属扩散膜将池体分割成a、b两室，但测定时间仍需1.5至4小时。该方法需要测量液体稳态时的浓度，操作时间较长，且该方法只能测量两种浓度相差较小的溶液间的扩散，不适用于多数情况下的扩散系数测定。

5、除此之外，云南大学物理与天文学院的陈艳学者基于液芯柱透镜的焦平面成像原理,用等折射率薄层移动法测量了不同体系以及不同浓度的扩散系数,并在此基础上利用matlab软件，基于光线追踪法，把扩散系数分别视为常数和随浓度变化的函数关系式对扩散图像进行仿真，验证了实验结果的准确性。这种测量方法测得的实验图像与仿真图像轮廓较为接近，测得的扩散系数较为准确，但这种测量方法实验工作量大，测量所耗时间较长，而且如果测量的二元溶液间折射率相差较大，将收集不到完整扩散图像。

技术实现思路

1、本发明的技术目的，是为了解决背景技术中的问题，提供一种自扩散式平面扩散系数测量方法。

2、本发明的实验原理如下：

3、菲克第一定律是描述扩散现象的基本方程。菲克第一定律指出，在任何浓度梯度驱动的扩散体系中，在单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量(j)与该截面处的浓度梯度成正比。数学表达式如下：

4、

5、其中，d为扩散系数，c为扩散物质的体积浓度，为浓度梯度，“-”号表示扩散方向为浓度梯度的反方向，即扩散组元由高浓度区向低浓度区扩散。

6、菲克第二定律是在第一定律的基础上推导出来的。菲克第二定律指出，在非稳态扩散过程中，在距离x处，浓度随时间的变化率等于该处的扩散通量随距离变化率的负值。数学表达式如下：

7、

8、如果扩散系数d随坐标x变化不大，可近似看成常数，该式可以写成：

9、

10、其中，c为扩散物质的体积浓度，t为扩散时间，x为距离。实际上，扩散系数d是随浓度变化的，为了使求解扩散方程简单些，往往近似地把d看作恒量处理。

11、运用菲克第一定律和第二定律计算扩散系数的方法较为常见，但浓度梯度往往难以求得，常常需要借助一些精密复杂的仪器，实验门槛较高，故需要优化测量方法，由此引出采用从分子动力学原理角度出发，通过均方位移计算扩散系数的方法，测定墨水移动距离与时间来计算扩散系数。

12、分子动力学是一种确定性模拟方法，按体系内部的内部动力学规律来计算并确定位形的转变，通过计算机，在原子量级上模拟材料的性质。模拟的根本问题是确定一群有相互作用的粒子在时空中的演化规律，通过建立数学模型，把关于微观粒子或粒子团的结构、粒子间力的知识与牛顿力学结合起来，指定粒子运动应遵循的自然规律和粒子间的相互作用的形式；再利用计算机计算粒子集合的相轨迹，从而确定系统的静态和动态性质。

13、分子动力学得天独厚的优势是能够模拟分子的运动轨道，即能够提供分子运动和变化的最为微观的、细致的信息，突破了传统的力学、热力学、光谱学等实验方法的制约。通过分子动力学计算得到运行轨道，就能通过直接的计算公式给出感兴趣的非平衡态物理量。正是这种不可替代的作用，使得分子动力学在当今自然科学研究中获得了广泛和深入的应用，占有重要地位。

14、原则上，分子动力学方法所适用的微观物理体系并无什么限制，适用的体系既可以是少体系统，也可以是多体系统；既可以是点粒子体系，也可以是具有内部结构的体系；处理的微观客体既可以是分子，也可以是其它的微观粒子。

15、分子动力学方法与蒙特卡洛方法一起已经成为计算机模拟的重要方法。应用分子动力学方法在气体或液体的状态方程、相变问题、以及非平衡过程的研究等多个研究领域都取得了许多重要成果。

16、从微观角度进行分析，首先需要建立一组分子的运动方程，并通过直接对系统中的一个个分子运动方程进行数值求解，得到每个时刻各个分子的坐标与动量，即在相空间的运动轨迹，再利用统计计算方法得到多体系统的静态和动态特性,从而得到系统的宏观性质。在这样的处理过程中可以看出：分子动力学方法中不存在任何随机因素。由于在处理过程中，方程组的建立是通过对物理体系的微观数学描述给出的，故系统的动力学机制决定了运动方程的形式。

17、流体中单一分子的运动并非沿着一个简单的路径，在它的移动过程中，它不断和其它分子发生碰撞并被推离原本的方向。如果进一步仔细观察它的路径，就会发现，这非常近似于数学上随机漫步。这种路径由爱因斯坦在对布朗运动的研究中进行了著名的分析，他发现：做随机漫步的粒子的移动距离的平方的平均数与时间成正比。这个关系式可以表示为：〈r〉2＝4dt+c。其中，〈r〉2是位移平方的平均，t是时间，d和c是常数。d是其中最重要的参数，又叫做扩散系数。

18、大多数情况下msd研究的是简单扩散模式，在此假定下求扩散系数的步骤是先计算msd,然后拟合msd线性部分的斜率,再除以4就是平面下的扩散系数。

19、记录第一帧的粒子位置作为初始位置，然后依次计算后续所有帧的粒子位置与初始位置的偏差，并对同种粒子进行加和求平均。其中一种粒子的msd计算公式如下：

20、

21、当体系处于液态时，均方位移与时间呈线性关系，平面情形下，其斜率与扩散系数存在下列关系：

22、

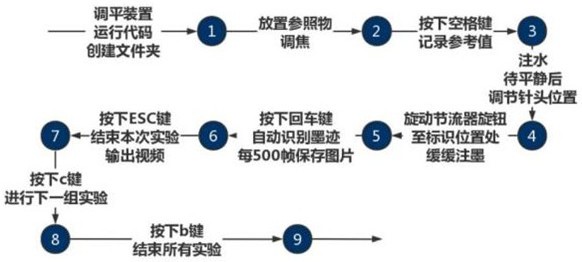
23、一种自扩散式平面扩散系数测量方法，采用均方位移msd法来测量平面下的液体扩散系数，机器识别测量操作流程为：

24、s1首先利用水平仪调平装置，打开摄像头，运行代码，先后输入f和数字在树莓派桌面上创建文件夹；

25、s2放置参照物，调节摄像头焦距直至图像清晰，并调节灯光使得摄像头能正常框选范围；

26、s3按下空格记录参考值；

27、s4向器皿中注水，待水面平静后，调节升降滴墨装置，将针管降至装置底部；

28、s5轻旋节流器旋钮，调至标识位置处，向装置缓缓注入墨水；

29、s6待装置稳定后，按下回车键，摄像头自动识别墨迹大小，每隔500帧保存一次图片并输出墨水扩散过程的视频录制，储存在文件夹中；

30、s7按下esc键自动结束本次实验，若需要重复实验，按下按键c，重复以上步骤进行下一组实验；

31、s8按下键盘上的按键b，结束所有实验录制；最后将得到的实验数据分析，计算出均方位移和坐标轴时间，计算得到扩散系数。

32、作为优选，所述s5注墨方式为使用带节流器的点滴输液器注入墨水。

33、采用本发明，优点在于传统的注墨方式一般为手推注射器注入墨水但是手推注墨可能会导致实验存在如下问题：1.手推装置不稳定，受外界干扰，使墨水不呈圆形扩散；2.由于液体表面张力的作用，液面顶部产生一圈墨晕；3.墨水初动能过大，需要很长时间才能达到稳定的扩散。进行多组手推注墨实验，分析实验数据得到，采用手推注射器注入墨水的方式得到的扩散系数与理论值存在30％至50％的相对误差。因此改进注墨方式，使用带节流器的点滴输液器注入墨水，为了尽量减小墨水扩散的初动能，从而实现墨水在清水中的平面自扩散，探究墨水初速度近似为零的条件。改变输液器滚轮位置，测量针头截面、流过的水的体积和所用时间，通过公式q＝s×v×t计算输液器出墨速度；滚轮位置与输液器出墨速度关系图如图2所示，可以看到其变化大致为一个二次函数，节流器旋钮位置数值越大说明节流器开口越大。利用该函数与x轴的交点，找到使得流速为0的旋钮位置在1.46cm处，并做好记录。之后将节流器旋钮调至该位置，可以使得从针管截面流出的流速近似为0，从而实现墨水初动能最小。

34、作为优选，所述s5注墨位置为将针头置于液面底部注入墨水进行实验，测定扩散系数。

35、采用本发明，优点在于将针头置于液面底部注入墨水时，针头出墨口与底部距离微小，墨水落下时受重力作用与容器底部的碰撞可忽略不计，从而在一定程度上减小了墨水扩散初动能的影响，使墨迹完整清晰。然而当将针头置于液面顶部注入墨水时，由于液体表面张力的影响，墨水与水面接触，墨水内表面活性剂减小了与墨接触水面的张力。与墨水接触的水面和外围一圈水面形成张力差，于是墨水受外围一圈水面的表面张力吸引而快速晕开。将针头置于液面中部注入墨水时，墨水落下时受重力作用，到达底部的过程中重力势能转化为动能，使得扩散初期受墨水流动影响较大，到达稳定的自扩散的时间长，容易出现扩散系数测定偏大。

36、作为优选，利用material studio软件模拟的过程参数为：计算1atm、25℃下水分子无定形体系的径向分布函数和扩散系数并进行分子动力学模拟，构建多分子水的无定型体系；利用amorphous cell模块，设置水分子数量，温度设置为298k，构建1个立方盒，设置celltype为periodiccell，水密度为0.997g/cc；选用compass力场；计算结束后即产生水分子无定形体系的轨迹。

37、作为优选，对构建的水分子无定形体系轨迹进一步优化，优化过程中设置参数为用discover模块对体系进行平衡计算，设定温度为298k，温度控制方法选择为nose，压力为0.0001gpa，压力控制方法为berendsen，步数设为10000，时间步长为1fs，计算结束后完成优化。

38、作为优选，对优化后的水分子无定形体系轨迹最后进行分析，分析过程为将所有h原子命名为h，用同样的方法将体系中的o原子命名为o，选中所有水分子命名为h2o，设置完成后对水分子进行分析。

39、作为优选，所述均方位移msd法计算方法为先以第一帧的粒子位置作为初始位置计算，然后依次计算后续所有帧的粒子位置与初始位置的偏差，并对同种粒子进行加和求平均，其中一种粒子的msd计算公式如下：

40、

41、当体系处于液态时，均方位移与时间呈线性关系，平面情形下，其斜率与扩散系数存在下列关系：

42、

43、即得到扩散系数d。

44、采用本发明，优点在于通过分析均方位移(msd)来间接求出体系的扩散系数，更加方便简洁，操作难度低。

45、作为优选，用一次性医用点滴输液器注射的方式代替传统的用注射器手动注射的方式，其中滑轮式开关作为流量调节器能够便捷地控制墨水注入的速度，斜口平整光滑的针头能够使墨水平稳地注射到容器底部。

46、作为优选，使用一个可进行上下左右调节的手摇杆来调节摄像头位置，使摄像头对准扩散装置；配合一个可升降的摇杆，摇杆与步进电机相连，步进电机上装有齿轮，齿轮卡在摇杆的缺口上，并将点滴输液器安装在可升降摇杆上。

47、作为优选，所述扩散装置整体放置于一个仅一端开口的木制外壳中，木壳内部周围防止亮度可调节灯带。

48、采用本发明，优点在于用一次性医用点滴输液器注射的方式代替传统的用注射器手动注射的方式，其中滑轮式开关作为流量调节器能够便捷地控制墨水注入的速度，斜口平整光滑的针头能够使墨水平稳地注射到容器底部；此外，为使摄像头识别出的图像清晰可视，设计了一个可进行上下左右调节的手摇杆来调节摄像头位置，使摄像头对准定制亚克力盒，保证摄像头能够成功框定定制的亚克力盒和墨水扩散图样，从而增加识别出的图像的准确度；设计了一个可升降的摇杆，摇杆与步进电机相连，步进电机上装有齿轮，齿轮卡在摇杆的缺口上。当按动装置上的按钮时，步进电机上的齿轮转动，从而带动摇杆的升降。再将点滴输液器安装在可升降摇杆上后，就可以通过控制摇杆的升降来调整输液器针头的高度，从而能够使墨水平稳地注射到容器底部，在一定程度上减小了人为手动注射不稳使液面晃动带来的误差。在利用摄像头识别墨水扩散边缘的过程中，可能会出现由于外部光线变化导致扩散图像边缘识别错误导致较大误差的情况。为了有效减小实验误差，将扩散装置整体放置于一个仅一端开口的木制外壳中，再在木制壳内部周围放置灯带，灯带与滑动变阻器相结合后，使得装置内的光强可以自由调控，从而能够人为调节到一个使摄像头识别所得图像清晰可视的亮度。

49、采用本发明，优点在于为了更精确测定扩散系数，在装置上增加摄像头作为辅助装置代替人眼读数，并在装置上方安装液晶显示屏以使扩散图片及视频显示在装置上，再通过树莓派和显示屏相结合，就能够脱离电脑，形成一个独立的装置。由于墨水总量有限，实验进行到后期，不断接近纯扩散时，由于墨水浓度不断降低，扩散图像的边缘将变得模糊，依靠人眼读数困难且容易造成较大误差，而利用摄像头识别，即使在浓度很低时，依然能够进行范围的框定，有效减少实验偶然误差。

50、综上，本发明的有益效果是：

51、1、利用与测量方法配套的扩散装置，通过点滴输液器、可调节手摇杆、可升降摇杆与亮度可调节灯带配合摄像头，装置设计简洁、操作便捷、结果可靠，能够更精确测定扩散系数，有效减少实验偶然误差；

52、2、装置配合ms软件均方位移的方法来测定扩散系数，通过分析均方位移(msd)来间接求出体系的扩散系数，简单可靠，过程简单。