一种基于改进神经网络的自动优化课程安排方法与流程

本发明涉及智慧课堂，尤其涉及一种基于改进神经网络的自动优化课程安排方法。

背景技术：

1、随着信息技术的发展和教育管理的日益复杂，课程安排已成为教育管理中的一个重要问题。在高等教育、职业教育和各类培训机构中，课程安排不仅需要考虑教师的时间表、教室的容量，还要兼顾学生的选课需求和课程的重要性。这些因素的复杂性和多变性使得传统的课程安排方法面临巨大的挑战。

2、现有的课程安排方法主要依赖于人工操作或简单的规则算法。在人工操作中，教育管理者通常通过经验和直觉来制定课程表，但这种方法效率低下且容易出错，特别是在面对大规模的数据和复杂的约束条件时。例如，教师的时间表可能会随时变化，教室的容量需要实时更新，学生的选课需求也会不断调整。这些复杂的因素使得人工操作难以快速、准确地生成最优的课程安排方案。

3、在规则算法方面，常用的方法包括线性规划、整数规划和启发式算法等。然而，这些方法通常只能解决较为简单的课程安排问题，对于多维度、多变量的复杂约束条件，效果并不理想。线性规划和整数规划需要将问题转化为数学模型，但由于课程安排问题的非线性和高维性，建模过程复杂且计算量巨大。启发式算法如遗传算法、模拟退火算法等虽然能够在一定程度上提高求解效率，但仍存在收敛速度慢、容易陷入局部最优等问题。

4、此外，现有的课程安排方法大多是静态的，即在生成课程表后，无法根据实际情况进行动态调整。一旦出现教师请假、学生选课变化等突发情况，需要重新进行排课，这不仅耗费时间，还容易导致课程安排的混乱。对于大型教育机构来说，课程安排的频繁变动将严重影响教学秩序和教育资源的利用率。

技术实现思路

1、本发明的一个目的在于提出一种基于改进神经网络的自动优化课程安排方法，本发明通过引入深度学习和优化算法，不仅解决了传统方法的不足，还显著提高了课程安排的效率和准确性。

2、根据本发明实施例的一种基于改进神经网络的自动优化课程安排方法，包括如下步骤：

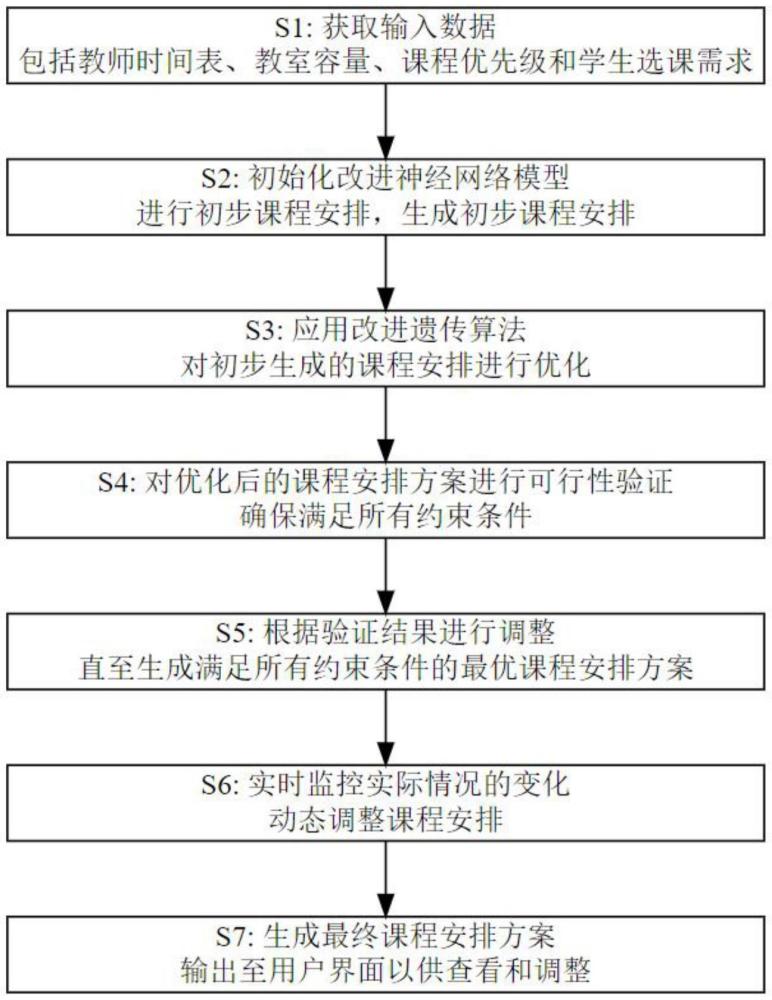
3、s1、获取输入数据，包括教师时间表、教室容量、课程优先级和学生选课需求；

4、s2、初始化改进神经网络模型，将获取的输入数据输入改进神经网络模型，进行初步课程安排，并初步生成课程安排；

5、s3、应用改进遗传算法对初步生成的课程安排进行优化：

6、s4、对优化后的课程安排方案进行可行性验证，确保满足所有约束条件；

7、s5、根据验证结果进行调整，直至生成满足所有约束条件的最优课程安排方案；

8、s6、在课程安排过程中实时监控实际情况的变化，利用改进神经网络模型和优化算法对课程安排进行动态调整；

9、s7、生成最终课程安排方案，并输出至用户界面以供查看和调整。

10、可选的，所述s1具体包括：

11、s11、获取教师时间表，包括每位教师的可用时间段及不可用时间段：

12、t＝{t1，t2，...，tn}；

13、其中，ti＝{ti1，ti2，...，tim}表示第i位教师的可用时间段，n表示教师总数，tij表示具体的时间段；

14、s12、获取教室容量，包括每个教室的最大容纳人数及教室的可用时间段：

15、c＝{c1，c2，...，ck}；

16、其中，cj＝(cj，{tj1，tj2，...，tjp})，k表示教室总数，cj表示第j个教室的最大容纳人数，tjl表示教室的具体可用时间段；

17、s13、获取课程优先级，包括每门课程的重要性等级及其对应的优先级：

18、p＝{p1，p2，...，pm}；

19、其中，pq＝(pq，lq)，m表示课程总数，pq表示第q门课程，lq表示该课程的重要性等级；

20、s14、获取学生选课需求，包括每位学生的选课意向及课程冲突信息：

21、d＝{d1，d2，...，dr}；

22、其中，ds＝{(ps1，ts1)，(ps2，ts2)，...，(psu，tsu)}，r表示学生总数，psi表示学生s选择的第i门课程，tsi表示该课程的具体时间段；

23、s15、将教师时间表t、教室容量c、课程优先级p和学生选课需求d输入至数据预处理模块，进行预处理，得到预处理后的教师时间表t′、教室容量c′、课程优先级p′和学生选课需求d′；

24、s16、构建输入数据集dinput，包括预处理后的教师时间表t′、教室容量c′、课程优先级p′和学生选课需求d′：

25、dinput＝{t′，c′,p′,d′}。

26、可选的，所述s2具体包括：

27、s21、初始化改进神经网络模型，所述改进神经网络模型包括输入层、关系图嵌入模块、特征融合模块和输出层；

28、s22、将输入数据集dinput输入至神经网络模型的输入层；

29、s23、在输入层中，分别将教师时间表t′、教室容量c′、课程优先级p′和学生选课需求d′进行特征提取和标准化处理，得到教师特征矩阵xt、教室特征矩阵xc、课程特征矩阵xp和学生特征矩阵xd；

30、s24、将教师特征矩阵xt、教室特征矩阵xc、课程特征矩阵xp和学生特征矩阵xd输入至关系图嵌入模块，构建表示教师、教室、课程和学生之间关系的图g，并对图g进行嵌入，嵌入操作表示为：

31、h＝graphembed(g，xt，xc，xp，xd)；

32、其中，图嵌入的具体为：

33、

34、其中，hi表示节点i的特征向量，n(v)表示节点v的邻居集合，w表示权重矩阵，b表示偏置向量，relu表示修正线性单元激活函数；

35、s25、将图嵌入模块输出的高维特征表示h输入至特征融合模块，特征融合模块通过多头注意力机制进行特征融合，表示为：

36、z＝multiheadattention(h)；

37、其中，多头注意力机制的具体为：

38、

39、multihead(q，k，v)＝concat(head1，head2，...，headh)wo；

40、

41、其中，q、k、v分别表示查询、键和值矩阵，和wo为权重矩阵，dk为缩放因子；

42、s26、将融合后的特征矩阵z输入至输出层，输出层由若干个全连接层组成，通过非线性变换生成初步课程安排方案ainitial，包括每门课程的时间安排、教室分配和教师分配；

43、s27、在输出层中，应用多目标损失函数l，包括资源利用率最大化、冲突最小化和优先级满足度，表示为：

44、l＝α·lresource+β·lconflict+γ·lpriority；

45、其中，θ、β和γ为权重系数，lresource表示资源利用率损失，lconflict表示冲突损失，lpriority表示优先级满足度。

46、可选的，所述资源利用率损失：

47、

48、其中，ui表示第i门课程的实际使用资源，ci表示第i门课程的最大可用资源，m表示课程总数；

49、所述冲突损失：

50、

51、其中，δ(ti，tj)表示第i门课程和第j门课程在时间安排上的冲突，若冲突则为1，否则为0，δ(ri，rj)表示在教室资源上的冲突，若冲突则为1，否则为0；

52、所述优先级满足度：

53、

54、其中，wi表示第i门课程的优先级满足度，pi表示第i门课程的优先级，di表示课程安排的优先级差异度，dmax表示最大优先级差异度。

55、可选的，所述s3具体包括：

56、s31、定义优化目标函数f，以最大化资源利用率u、最小化冲突c和最小化违约v为目标，优化目标函数表示为：

57、f＝α·u-β·c-y·v；

58、其中，α、，和γ为权重系数；

59、s32、初始化遗传算法的初始参数，包括种群大小n、交叉概率和变异概率；

60、s33、将初步生成的课程安排ainitial作为初始种群g＝{a1，a2，...，an}，每个个体ai进行编码表示；

61、ai＝(ai1，ai2，...，aim)；

62、其中，aij表示第i个个体中第j门课程的安排；

63、s34、计算初始种群中每个个体的适应度值f(ai)，根据优化目标函数f评估其优劣；

64、f(ai)＝α·u(ai)-β·c(ai)-γ·v(ai)；

65、s35、采用轮盘赌选择法选择适应度值较高的个体p(ai)进入下一代；

66、s36、采用多点交叉对选择的个体进行交叉操作，生成新的个体；

67、anew＝crossover(ap，aq)；

68、其中，ap和aq为选择的父代个体，anew为交叉操作生成的新个体；

69、交叉操作过程为：

70、anew＝(ap1，ap2，...，apk，aq(k+1)，aq(k+2)，...，aqm)；

71、其中，k为交叉点的位置；

72、s37、采用自适应变异对交叉后生成的个体进行变异操作；

73、amut＝mutation(anew)；

74、其中，amut为变异后的新个体；

75、变异操作过程为：

76、amut＝(ax，a2，...，aj-1，a′j，aj+1，...，am)；

77、其中，a′j为第j个基因的变异；

78、s38、计算新一代种群中每个个体的适应度值f(amut)，根据优化目标函数f评估其优劣；

79、s39、对比新一代种群中的个体与当前最优个体abest，选择适应度值最高的个体作为新的最优课程安排；

80、

81、s310、重复s35至s39，直至达到预设的迭代次数或满足终止条件；

82、s311、输出优化后的课程安排方案aopt。

83、可选的，所述资源利用率u表示为：

84、

85、所述冲突c表示为：

86、

87、所述违约v表示为：

88、

89、其中，vij表示第i门课程和第j位教师在课程安排中的违约情况，若违约则为1，否则为0。

90、可选的，所述s4具体包括：

91、s4l、对优化后的课程安排方案aopt进行时间约束验证，确保每门课程的时间安排不与教师和教室的可用时间冲突，验证条件表示为：

92、

93、其中，tij表示第i门课程在第j教室的时间安排，ti表示第i位教师的可用时间段，cj表示第j个教室的可用时间段；

94、s42、对优化后的课程安排方案aopt进行教室容量验证，确保每门课程的实际选课人数不超过教室的最大容纳人数，验证条件表示为：

95、

96、其中，di表示第i门课程的实际选课人数，cj表示第j个教室的最大容纳人数；

97、s43、对优化后的课程安排方案aopt进行课程优先级验证，确保每门课程的重要性等级符合预期，验证条件表示为：

98、

99、其中，pi表示第i门课程的优先级，li表示第i门课程的重要性等级；

100、s44、对优化后的课程安排方案aopt进行学生选课需求验证，确保每位学生的选课需求得到满足，验证条件表示为：

101、

102、其中，psi表示学生s选择的第i门课程，ds表示学生s的选课需求集合；

103、s45、对优化后的课程安排方案aopt进行冲突验证，确保没有课程在同一时间段安排在同一教室或由同一教师授课，验证条件表示为：

104、

105、其中，tij表示第i门课程在第j教室的时间安排，tik表示第i门课程由第k位教师授课，tkj表示第k门课程在第j教室的时间安排；

106、s46、根据验证结果对aopt进行必要调整，直至所有约束条件均得到满足，生成最终的最优课程安排方案afinal。

107、本发明的有益效果是：

108、(1)本发明通过改进神经网络模型，能够有效处理教师时间表、教室容量、课程优先级和学生选课需求等多维度、多变量的复杂约束条件。相比于传统的线性规划和整数规划方法，本发明能够在更短的时间内生成更优化的课程安排方案，显著提高了系统的计算效率和排课质量。

109、(2)本发明利用改进的神经网络模型和遗传算法，对初步生成的课程安排方案进行优化。通过定义优化目标函数，以最大化资源利用率、最小化冲突和违约为目标，确保生成的课程安排方案在各方面均达到最优状态，充分利用了教育资源。

110、(3)本发明能够实时监控实际情况的变化，如教师请假、学生选课变化等，利用改进神经网络模型和优化算法对课程安排进行动态调整，确保在突发情况下依然能够维持最优的安排方案。这种动态调整能力显著优于传统的静态排课方法，使得系统具备了高度的灵活性和适应性。

111、(4)本发明通过多目标优化算法，综合考虑资源利用率、冲突和违约等多个因素，采用多点交叉和自适应变异等技术手段，进一步提高了课程安排的质量。通过对优化后的课程安排方案进行可行性验证，确保最终方案满足所有约束条件，从而实现了多目标优化的效果。