具备减小偏差能力的低复杂度三维AOA移动目标定位方法

本发明涉及一种目标定位技术，尤其是涉及一种传感器位置部分已知的具有减小偏差能力的三维aoa(angle-of-arrival)移动目标定位方法。

背景技术：

1、在过去的几十年里，目标定位技术已在多个领域实现了广泛的应用，包括但不限于目标跟踪、自动驾驶、搜索与救援以及无线通信等。其中，信号的到达角(angle ofarrival，aoa)定位方法因其低廉的价格和定位精度高的优势已成为目标定位领域的热门研究主题。

2、现存的aoa定位方法需要对模型进行转换，然而，转换过程中通常会引入大量偏差，从而会给移动目标的位置和速度的估计带来不容忽视的影响。现有的考虑减小偏差的研究方法通常采用最大似然的方法或半正定松弛的方法对目标位置进行估计，但是最大似然的方法通常需要先验知识且在变量维度大、初始解不准确的情况下会陷入局部解；而半正定松弛的方法往往需要较高的计算复杂度，在实际工程领域并不适用。

3、现有的研究中，通常考虑所有传感器的位置都是已知的，这适用于固定地面站或可通过gps等技术获取位置的情况。然而，在诸如室内或水下等实际应用场景中，gps信号的缺失可能导致部分传感器的位置信息未知。因此，针对部分传感器位置未知的定位问题，值得进一步深入探索。现有文献对未知部分传感器位置情形下利用aoa进行定位的方法少有研究，而在传感器全部已知情况下的aoa定位方法对于测量噪声十分敏感，且对定位场景的几何分布要求较高。

技术实现思路

1、本发明所要解决的技术问题是提供一种传感器位置部分已知的具有减小偏差能力的三维aoa移动目标定位方法，其在不需要任何先验信息的前提下，使用aoa的测量信息在传感器位置部分已知的情况下对未知位置的传感器和移动目标进行联合定位，对定位场景的几何分布没有要求，且对测量噪声表现出很好的鲁棒性。

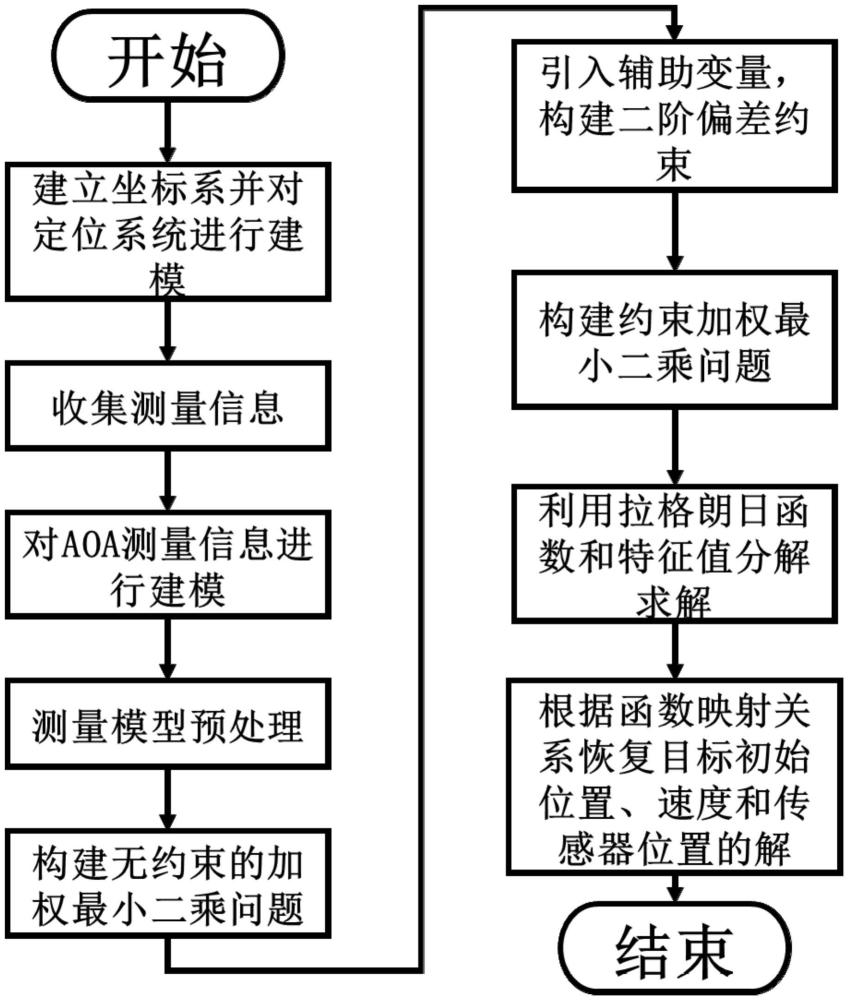
2、本发明解决上述技术问题所采用的技术方案为：一种具备减小偏差能力的低复杂度三维aoa移动目标定位方法，其特征在于包括以下步骤：

3、步骤1：在传感器网络中，建立一个三维坐标系作为参考坐标系，并设定存在j个传感器和一个匀速直线运动的移动目标，第1个传感器至第n个传感器的位置已知，第n+1个传感器至第j个传感器的位置未知，移动目标的初始位置和移动速度均未知，设定移动目标共移动k个时刻；任意一个已知位置的传感器在参考坐标系中的真实位置设定为参考坐标系的原点，当1≤i≤n时将第i个已知位置的传感器在参考坐标系中的真实位置记为si，si＝[sx,i,sy,i,sz,i]t，当n+1≤i≤j时将第i个未知位置的传感器在参考坐标系中的真实位置记为将移动目标在参考坐标系中的真实初始位置记为将移动目标的真实移动速度记为vo，将移动目标在第k个时刻在参考坐标系中的真实位置记为其中，k＞1，i＝1,...,j，sx,i,sy,i,sz,i对应表示si的横坐标、纵坐标、竖坐标，上标“t”表示向量或矩阵的转置，对应表示的横坐标、纵坐标、竖坐标，对应表示的横坐标、纵坐标、竖坐标，对应表示vo的沿参考坐标系的x轴的速度分量、沿参考坐标系的y轴的速度分量、沿参考坐标系的z轴的速度分量，k＝1,...,k，表示时间间隔；

4、步骤2：在传感器网络中，移动目标在第k个时刻发射的信号被第i个传感器接收，第i个传感器获得到达信号的受噪声污染的aoa测量值，aoa测量值包括方位角测量值和俯仰角测量值，对应记为θk,i和φk,i；其中，k＝1,...,k，i＝1,...,j；

5、步骤3：构建移动目标发射的信号被已知位置的传感器接收后获得的到达信号的aoa测量模型，描述为：

6、

7、并构建移动目标发射的信号被未知位置的传感器接收后获得的到达信号的aoa测量模型，描述为：

8、

9、其中，θk,i即为移动目标在第k个时刻发射的信号被第i个传感器接收后获得的到达信号的受噪声污染的方位角测量值，表示移动目标在第k个时刻发射的信号被第i个传感器接收后获得的到达信号的方位角真实值，表示移动目标在第k个时刻发射的信号被第i个传感器接收后获得的到达信号的方位角测量噪声，φk,i即为移动目标在第k个时刻发射的信号被第i个传感器接收后获得的到达信号的受噪声污染的俯仰角测量值，表示移动目标在第k个时刻发射的信号被第i个传感器接收后获得的到达信号的俯仰角真实值，表示移动目标在第k个时刻发射的信号被第i个传感器接收后获得的到达信号的俯仰角测量噪声，当1≤i≤n时rk,i表示移动目标与第i个已知位置的传感器在参考坐标系的x-o-y平面上的二维距离，当n+1≤i≤j时表示移动目标与第i个未知位置的传感器在参考坐标系的x-o-y平面上的二维距离，

10、步骤4：对式(1)进行预处理：忽略式(1)的两个等式中的噪声项，并取正切得到然后将式(1.1)的两个等式各自的两边交叉相乘并整理得到

11、再根据对式(1.2)的两个等式中的正弦项和余弦项进行一阶泰勒展开，得到

12、对式(2)进行预处理：忽略式(2)的两个等式中的噪声项，并取正切得到然后将式(2.1)的两个等式各自的两边交叉相乘并整理得到再根据对式(2.2)的两个等式中的正弦项和余弦项进行一阶泰勒展开，得到

13、步骤5：联立式(1.3)和式(2.3)，构建由传感器位置部分已知的联合定位的加权最小二乘问题，描述为：

14、

15、其中，为加权最小二乘问题的优化变量，表示移动目标的初始位置变量，表示移动目标的移动速度变量，表示第i个未知位置的传感器的位置变量，为加权最小二乘问题的目标函数，为系数矩阵，中的第k个子矩阵为的第i行向量为的第i行向量为0n×3m表示维度为n×3m的全0矩阵，n表示已知位置的传感器的数量，m表示未知位置的传感器的数量，m＝j-n，blkdiag()为求块对角矩阵函数，中的第i-n个块对角子矩阵为中的第i-n个块对角子矩阵为为引入的系数向量，的第k列向量为01×m表示维度为1×m的全0向量，的第i元素为的第i元素为为引入的权重矩阵，表示求数学期望，为引入的系数矩阵，中的第k个块对角子矩阵为diag()为求对角矩阵函数，|| ||为二范数运算符号，表示测量噪声向量，的第k个子向量为服从均值为0且协方差矩阵为的高斯分布，表示的协方差矩阵，的协方差矩阵为

16、步骤6：在步骤5构建的加权最小二乘问题中引入新的辅助变量将步骤5构建的加权最小二乘问题的目标函数转换为然后定义和将转换为再将拆分成由真实值和误差构建的矩阵，即：最后将引入中，得到：其中，中的θk,i和φk,i对应替换为和后得到中的第k个子矩阵为的第i行向量为的第i行向量为中的第i-n个块对角子矩阵为中的i-n个块对角子矩阵为中的θk,i和φk,i对应替换为和后得到的第k列向量为的第i个元素为的第i个元素为的第i行向量为的第i行向量为的第i行向量为中的第i-n个块对角子矩阵为中的第i-n个块对角子矩阵为中的第i-n个块对角子矩阵为v＝blkdiag(v1,...,vk)，v中的第k个块对角子矩阵为vk，⊙为哈达玛积运算符号，表示中的第1行至第j行和第1列至第j列构成的子矩阵，表示中的第j+1行至第2j行和第j+1列至第2j列构成的子矩阵，表示中的第1行至第j行和第j+1列至第2j列构成的子矩阵，由得到，表示中的第k个块对角子矩阵，的第k列向量为的第i元素为的第i元素为的第i元素为

17、步骤7：在步骤6的基础上，构建在传感器位置部分已知情况下的具有减小偏差能力的约束加权最小二乘问题，描述为：

18、

19、其中，为约束加权最小二乘问题的优化变量，的维数为(7+3m)×1，表示一个常数；

20、步骤8：对步骤7构建的约束加权最小二乘问题构造拉格朗日函数，表示为：然后根据拉格朗日函数采用kkt条件，得到带有的最优解的式子再对采用特征值分解，分解出最后根据得到移动目标的初始位置变量的估计值移动目标的移动速度变量的估计值第i个未知位置的传感器的位置变量的估计值其中，l()表示拉格朗日函数，为拉格朗日乘子，表示的第1个元素至第3个元素构成的向量，表示的第7+3m个元素，表示的第4个元素至第6个元素构成的向量，表示的第4+3(i-n)个元素至第6+3(i-n)个元素构成的向量。

21、与现有技术相比，本发明的优点在于：

22、1)在现有的研究中，传感器布置的位置通常被假定为已知，然而，在gps信号无法覆盖的环境下，如水下、地下或室内定位场景，传感器的位置信息可能无法获取，值得注意的是，对于aoa测量信息的获取，并不需要确切知道传感器的绝对位置，这为未来的研究开辟了新的可能性。

23、2)传统的aoa定位方法在模型转换过程中往往会产生较大的偏差，本发明方法通过在由传感器位置部分已知的联合定位的加权最小二乘问题中引入新的辅助变量，并将二阶偏差作为约束条件进行考虑，成功降低了偏差，使得定位精度得到了显著的提升。

24、3)本发明方法在不需要任何先验信息的前提下，巧妙地利用角度测量信息来构造俯仰角，从而极大地简化了原本复杂且非线性的距离测量模型，这种方法不仅减少了耦合变量的数量，还能通过构造拉格朗日函数和特征值分解的方法获得闭式解，计算复杂度低。

25、4)现有的移动目标定位方法对于定位场景的几何分布要求较高，当定位场景的几何分布对于估计精度不利时，使得该方法的定位性能急剧下降，而本发明方法对于定位场景的几何分布在任意定位场景下都能够表现出较好的定位性能。

26、5)本发明方法的实验结果显示，其可以达到克拉美-罗下界(crlb)的定位精度，表现出稳定的性能。对于测量噪声表现出了极好的鲁棒性，即使在测量噪声功率较大的情况下，它依然能够展现出鲁棒的定位性能。此外，值得一提的是，即便未知位置的传感器数量增加，本发明方法的性能也并不会受到负面影响，反而可能进一步提高已存在的移动目标的定位精度。