一种卫星相位偏差解算方法、系统、设备及存储介质

本发明属于卫星信号处理，具体涉及一种卫星相位偏差解算方法、系统、设备及存储介质。

背景技术：

1、全球卫星导航系统（global navigation satellite system，简称gnss）的发展为高精度定位技术带来了革命性变化，作为其中代表性的精密单点定位（precise pointpositioning，简称ppp）技术以其单台 gnss接收机实现高精度定位、不受作用距离限制、作业机动灵活等诸多显著优点，已经被广泛应用于诸多工程应用和科学研究领域，具有重要的研究和应用价值。

2、然而，较长的首次初始化时间（bds-3 ppp首次初始化时间在30分钟左右）一直是制约ppp技术发展的瓶颈问题，限制了其在变形监测、点位坐标采集等传统高精度定位领域，以及自动（辅助）驾驶、无人机和可穿戴设备等新兴的高精度定位领域中的应用。ppp较长的首次初始化时间主要是因为在ppp解算中同时包含了接收机三维位置、接收机钟差、大气延迟误差以及整周模糊度等过多的待求参数，使得待求参数之间的相关性增强，需要较长时间积累足够多而有效的观测信息才能精确分离各类待求参数。近20多年来，虽然许多学者从定位模型、误差模型精化、非差整数模糊度固定以及质量控制等方面，针对如何缩短ppp首次初始化时间展开了细致的研究，但在无密集参考站增强的情况下，仍未解决这一难题。

3、随着“pnt”以及“通讯、导航和遥感一体化”等空间战略的发展，低轨（low earthorbit，简称 leo）星座已被列入我国第四代卫星导航建设计划，进入了蓬勃的发展期。相比bds-3星座，leo星座卫星运行速度快、使得卫星与接收机间的几何构型迅速变化，能够快速削弱参数间的相关性，对增强bds-3的定位精度、收敛时间具有显著优势，有望从根本上解决ppp快速首次初始化这一难题。最近几年，一些学者对leo增强bds或multi-gnssppp进行了研究，结果表明，融合leo观测数据后，ppp浮点解的收敛时间可由30分钟缩短至1分钟以内，并且收敛性能改善的程度取决于低轨卫星的数量以及低轨卫星的空间几何分布，以上研究论证了leo卫星增强ppp的可行性，有望从根本上解决ppp快速首次初始化这一难题。

4、但是，纵观国内外研究现状，目前有关leo增强ppp的研究主要聚焦于ppp浮点解，对于leo星座增强ppp固定解的研究十分有限，如上所述，相比ppp浮点解，ppp固定解定位精度更高，更重要的是，在ppp固定解中具有一套能判定定位结果可靠性的检验指标，因而定位结果具有更高的可靠性，这在涉及生命安全场景（如自动驾驶）的实时动态定位至关重要，因此，十分有必要对leo星座增强ppp固定解进行深入研究。然而，若要实现leo/bds-3异构星座ppp固定解，高精度卫星相位偏差产品是其前提。但是，由于leo卫星高动态、短弧段观测条件，使其在ppp服务端数据利用率低，提取出的浮点模糊度弧段短，精度难以保证，给leo卫星相位偏差精确估计带来了不确定性。

技术实现思路

1、为了现有偏差解算方法给leo卫星相位偏差精确估计带来的不确定性问题，本发明提供了一种卫星相位偏差解算方法、系统、设备及存储介质。

2、为了实现上述目的，本发明提供如下技术方案：

3、一种卫星相位偏差解算方法，包括以下步骤：

4、获取leo/bds-3异构星座观测数据；

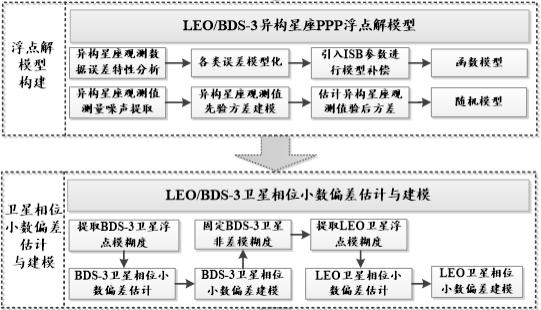
5、对leo/bds-3异构星座观测数据进行误差特性分析，根据分析结果对各类误差进行模型化，并引入系统性偏差isb参数进行模型补偿，构建浮点解函数模型；同时提取leo/bds-3异构星座观测数据的测量噪声，并根据测量噪声确定异构星座观测值先验方差、评估异构星座观测值验后方差，根据异构星座观测值先验方差和异构星座观测值验后方差构建随机模型；所述浮点解函数模型和随机模构成leo/bds-3异构星座ppp模型；

6、基于leo/bds-3异构星座ppp模型估计bds-3浮点模糊度，基于bds-3浮点模糊度估计出bds-3卫星相位偏差；

7、利用所述bds-3卫星相位偏差固定bds-3非差整数模糊度，并用已固定的bds-3非差整数模糊度约束leo/bds-3异构星座ppp模型，解算出leo浮点模糊度；利用所述leo浮点模糊度估计leo卫星相位偏差。

8、优选地，所述根据分析结果对各类误差进行模型化，并引入系统性偏差isb参数进行模型补偿，补偿关系表达式如下：

9、（1）

10、式中，tl为 leo接收机钟差参数，tc为 bds-3接收机钟差参数，isbc−l为leo/bds-3卫星系统性偏差之和。

11、优选地，确定异构星座观测值先验方差具体为：

12、采用零基线历元间差分方法，其测量噪声模型表达为：

13、

14、式中，和分别表示各类星座历元i双差伪距观测值和双差载波相位观测值；在得到各星座伪距和相位观测值噪声序列后，分别建立其标准差σ与卫星高度角e的函数，函数表达式为：

15、

16、式中，a和b为模型拟合常系数，通过最小二乘拟合或minque法求得，完成先验标准差模型建立，根据先验标准差模型确定异构星座观测值先验方差。

17、优选地，所述估计异构星座观测值验后方差，具体为：

18、将异构星座融合的ppp观测模型分成四类独立观测值la、lb、lc以及ld，并基于已建立的geo、igso、meo、leo各星座先验标准差模型，求取其先验方差，确定各星座观测值的初权pa、pb、pc和pd，其误差方程和初权表示为：

19、（4）

20、式中，、、和表示基于各类观测值先验标准差模型求取的方差；m为任意常数，、、、为各类观测值所形成的误差方程的系数阵，为函数模型中的待估参数；

21、同时，有下列关系式：

22、（5）

23、式中，n为由（4）式各误差方程所构造的法方程的系数阵，w为法方程的常数项；

24、按照上式进行间接平差，得、、和；然后，顾及数据解算效率，采用简化赫尔默特方差分量估计方法求取各类观测值单位权误差，其表达式如下：

25、（6）

26、式中，、、、分别为各类观测值的验后方程；、、和分别为各类观测值的数量；

27、根据求得的各类观测值单位权重误差和初权，对各类观测值重新定权重分别为、、和，其表达式如下：

28、（7）

29、重复上述步骤，即定权-平差-方差分量估计-再定权-再平差的过程，迭代至，从而完成异构星座各类观测值验后方差及其权比的确定。

30、优选地，所述基于leo/bds-3异构星座ppp模型估计bds-3浮点模糊度，基于bds-3浮点模糊度估计出bds-3卫星相位偏差，包括以下步骤：

31、采用leo/bds-3异构星座ppp模型进行 ppp浮点解解算，求解出leo浮点模糊度；

32、（8）

33、式中，表示ppp浮点解参数；b为leo/bds-3异构星座ppp模型构造的误差方程系数阵；p为其误差方程的权阵，由（7）式得出；l为误差方程的常数项；n和w表示对应的法方程的系数阵和常数项；

34、利用已经估计出的bds-3卫星相位偏差，进行bds-3非差整数模糊度固定，得到bds-3非差整数模糊度，并将其作为虚拟观测方程约束原ppp浮点解；

35、（9）

36、（10）

37、式（9）表示bds-3非差整周模糊度虚拟误差方程，其中为其误差方程的系数阵；为其误差方程的常数项；

38、式（10）中表示bds-3非差整周模糊度约束后的ppp浮点解参数；

39、从bds-3非差整数模糊度约束后的ppp浮点解中提取leo浮点模糊度，然后按照类似bds-3卫星相位偏差估计方法依次估计超宽巷、宽巷和窄巷卫星相位偏差。

40、优选地，还包括对bds-3和leo卫星相位偏差进行建模，包括以下步骤：

41、采用逐历元估计的策略获取geo、igso、meo和leo四类星座超宽巷/宽巷/窄巷卫星相位偏差估值时间序列；

42、基于多天的卫星相位小数估值时间序列，统计各类星座超宽巷/宽巷/窄巷卫星相位偏差估值变化超过0.1周阈值所用时间，确定其时间窗口；

43、基于时间窗口统计结果，分别建立geo、igso、meo和leo四类星座超宽巷/宽巷/窄巷卫星相位偏差分段常数模型。

44、本发明还提供一种卫星相位偏差解算系统，包括：

45、数据获取模块，用于获取leo/bds-3异构星座观测数据；

46、第一建模单元，用于对leo/bds-3异构星座观测数据进行误差特性分析，根据分析结果对各类误差进行模型化，并引入系统性偏差isb参数进行模型补偿，构建浮点解函数模型；

47、模型构建单元，用于对leo/bds-3异构星座观测数据进行误差特性分析，根据分析结果对各类误差进行模型化，并引入系统性偏差isb参数进行模型补偿，构建浮点解函数模型；同时提取leo/bds-3异构星座观测数据的测量噪声，并根据测量噪声确定异构星座观测值先验方差、评估异构星座观测值验后方差，根据异构星座观测值先验方差和异构星座观测值验后方差构建随机模型；所述浮点解函数模型和随机模构成leo/bds-3异构星座ppp模型；

48、第一偏差估计单元，用于基于leo/bds-3异构星座ppp模型估计bds-3浮点模糊度，基于bds-3浮点模糊度估计出bds-3卫星相位偏差；

49、第二偏差估计单元，用于利用所述bds-3卫星相位偏差固定bds-3非差整数模糊度，并用已固定的bds-3非差整数模糊度约束leo/bds-3异构星座ppp模型，解算出leo浮点模糊度；用于利用所述leo浮点模糊度估计leo卫星相位偏差。

50、本发明还提供一种计算机设备，包括存储器、处理器及存储在存储器上的计算机程序，所述处理器执行所述计算机程序以实现所述非差整数模糊度辅助卫星相位偏差解算方法中任一项所述的步骤。

51、本发明还提供一种计算机可读存储介质，所述存储介质上存储有计算机程序，其特征在于，该计算机程序被处理器加载时，能够执行所述非差整数模糊度辅助卫星相位偏差解算方法中任一项所述的步骤。

52、本发明提供的非差整数模糊度辅助卫星相位偏差解算方法具有以下有益效果：

53、本发明首先构建了浮点解函数模型和随机模型，基于上述模型构成了异构星座融合的leo/bds-3异构星座ppp模型，降低了对leo可见星数的要求，服务端测站的选择更加灵活，增加了数据的可用性，同时融合的ppp模型中由于bds-3观测值的辅助特性，提高了leo短弧度浮点模糊度估计的精度，将bds-3非差整数模糊度固定并将其约束到ppp浮点解，也进一步提高了leo浮点模糊度精度，为leo卫星相位偏差精确快速解算提供有力保障。