一种受限玻尔兹曼机形式的可逆逻辑门的构建方法

本申请属于可逆逻辑门设计相关，更具体地，涉及一种受限玻尔兹曼机形式的可逆逻辑门的构建方法。

背景技术：

1、机器学习(ml)和人工智能(ai)凭借其高认知能力和强大的工具，最近在各个领域变得越来越流行，但是数据中心的强大计算能力建立在能源和碳的使用量显著增加的基础上，且由于半导体缩放的物理限制，我们很难降低这些计算的能耗。而概率计算是解决当前基于布尔逻辑的计算机系统能耗问题的有效方法之一。

2、受限玻尔兹曼机是实现概率计算的一种常用模型，其具有两层结构，分别为可见层和隐藏层，每层具有若干神经元节点，每个神经元节点为由概率计算单元(p-bit)构成的二值节点，逻辑门的变量输入可见层，经可见层与隐藏层的概率计算后在可见层输出符合逻辑门的因变量。

3、目前，利用受限玻尔兹曼机实现可逆逻辑门时，需要利用大量数据训练受限玻尔兹曼机模型来学习可逆逻辑，以确定受限玻尔兹曼机模型的参数，而通过训练的方式确定模型参数存在耗时较长且学习可能陷入局部最优的问题。

技术实现思路

1、针对现有技术的以上缺陷或改进需求，本申请提供了一种受限玻尔兹曼机形式的可逆逻辑门的构建方法，其目的在于通过计算直接确定受限玻尔兹曼机模型的参数，无需进行训练，由此解决通过训练的方式确定模型参数存在耗时较长且学习可能陷入局部最优的问题。

2、为实现上述目的，按照本申请的一个方面，提供了一种受限玻尔兹曼机形式的可逆逻辑门的构建方法，包括：

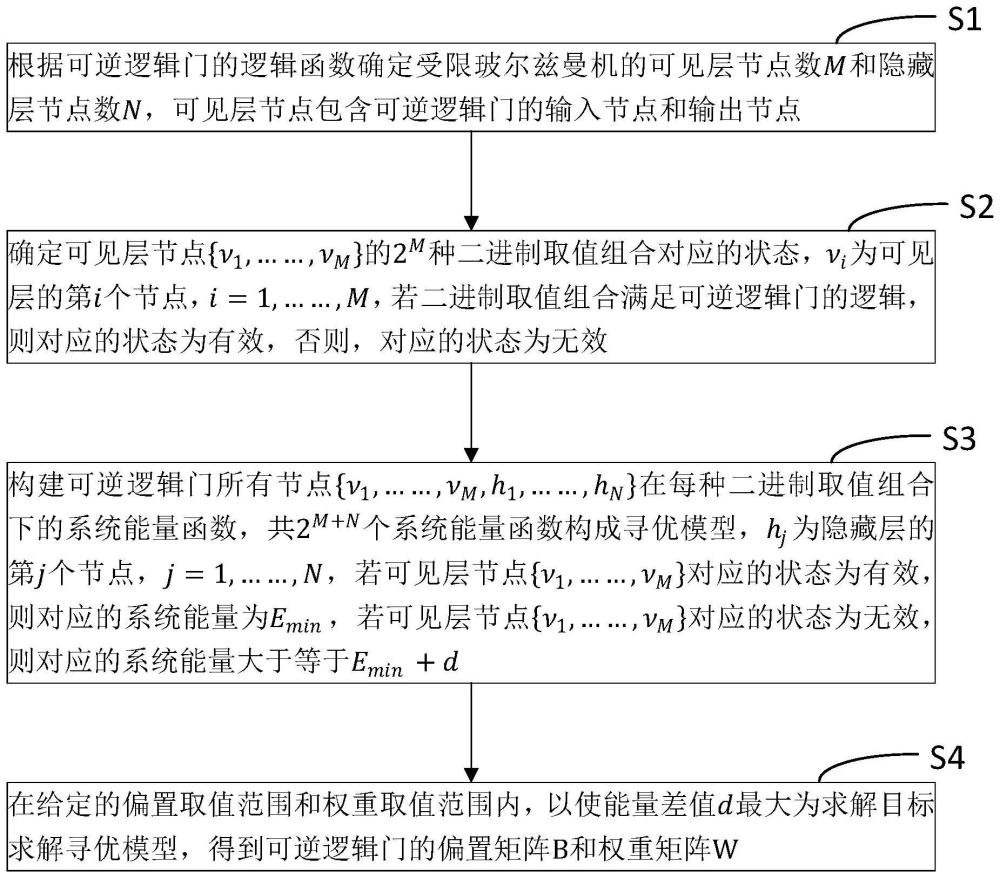
3、根据可逆逻辑门的逻辑函数确定受限玻尔兹曼机的可见层节点数m和隐藏层节点数n，可见层节点包含所述可逆逻辑门的输入节点和输出节点；

4、确定可见层节点{v1,……,vm}的2m种二进制取值组合对应的状态，vi为可见层的第i个节点，i＝1,……,m，若二进制取值组合满足所述可逆逻辑门的逻辑，则对应的状态为有效，否则，对应的状态为无效；

5、构建所述可逆逻辑门所有节点{v1,……,vm,h1,……,hn}在每种二进制取值组合下的系统能量函数，共2m+n个系统能量函数构成寻优模型，hj为隐藏层的第j个节点，j＝1,……,n，若可见层节点{v1,……,vm}对应的状态为有效，则对应的系统能量等于emin，若可见层节点{v1,……,vm}对应的状态为无效，则对应的系统能量大于等于emin+d；第k个系统能量函数式中，ai、分别为可见层的第i个节点的偏置和双极能量计算值，bj、分别为隐藏层的第j个节点的偏置和双极能量计算值，若节点的二进制取值为1，则对应的能量计算值为1，若节点的二进制取值为0，则对应的能量计算值为-1，wij为可见层的第i个节点与隐藏层的第j个节点的连接权重，偏置矩阵b＝[a1,……,am,b1,……,bn]、权重矩阵能量最小值emin和能量差值d为待求解量；

6、在给定的偏置取值范围和权重取值范围内，以使能量差值d最大为目标求解所述寻优模型，得到所述可逆逻辑门的偏置矩阵b和权重矩阵w。

7、在其中一个实施例中：利用线性规划方法求解所述寻优模型。

8、在其中一个实施例中：利用python中的lp工具pulp求解所述寻优模型。

9、在其中一个实施例中：隐藏层节点数n与可见层节点数m的关系为：n≤m-1。

10、在其中一个实施例中：所述受限玻尔兹曼机各节点的神经元的激活函数为取值从-1到1的双曲正切函数。

11、在其中一个实施例中：所述受限玻尔兹曼机各节点的神经元由自旋电子器件构成。

12、在其中一个实施例中：给定的偏置取值范围为-4～+4，给定的权重取值范围为-4～+4。

13、按照本申请的另一方面，提供了一种电子设备，包括存储器和处理器，所述存储器存储有计算机程序，所述处理器执行所述计算机程序时实现如上所述的方法的步骤。

14、按照本申请的另一方面，提供了一种计算机可读存储介质，其上存储有计算机程序，所述计算机程序被处理器执行时实现如上所述的方法的步骤。

15、总体而言，通过本申请所构思的以上技术方案与现有技术相比，本申请提供的受限玻尔兹曼机形式的可逆逻辑门的构建方法主要具有以下有益效果：

16、1.本申请提供的受限玻尔兹曼机形式的可逆逻辑门的构建方法，根据逻辑函数确定节点数量，根据逻辑门真值表确定不同二进制组合的状态，根据不同的状态将所有情形的能量函数值也分为对应的两种，当可见层输入输出节点的二进制取值满足可逆逻辑门，则认定为有效，此时，受限玻尔兹曼机模型的能量为最低值，而当可见层输入输出节点的二进制取值不满足可逆逻辑门，则认定为无效，此时，受限玻尔兹曼机模型的能量较大，这种不同状态下的能量关系符合受限玻尔兹曼机模型的工作机制，有效和无效之间的能量差异越大，则模型的准确度越高，其输出结果为正确答案的概率越大。因此，以受限玻尔兹曼机系统的能量函数构建成寻优模型，以两种状态下的能量差值最大为目标求解寻优模型，便能直接得到受限玻尔兹曼机的模型参数，包括同一层的节点偏置和不同层之间的节点连接权重，代入所确定的参数，便能得到受限玻尔兹曼机形式的可逆逻辑门。以上方法通过计算直接确定受限玻尔兹曼机模型参数，无需进行训练，因此，可以快速确定参数且不会出现学习可能陷入局部最优的问题。

17、2.本申请一实施例提供的受限玻尔兹曼机形式的可逆逻辑门的构建方法，在进行模型求解时，具体采用线性规划方法求解，如此，可以快速准确地实现模型的求解。

18、3.本申请一实施例提供的受限玻尔兹曼机形式的可逆逻辑门的构建方法，其受限玻尔兹曼机各节点的神经元的激活函数为取值从-1到1的双曲正切函数，实验证明，该计算方法对于该类型的神经元的适用性更佳，更能得到准确的模型参数。

技术特征：

1.一种受限玻尔兹曼机形式的可逆逻辑门的构建方法，其特征在于，包括：

2.如权利要求1所述的受限玻尔兹曼机形式的可逆逻辑门的构建方法，其特征在于：利用线性规划方法求解所述寻优模型。

3.如权利要求2所述的受限玻尔兹曼机形式的可逆逻辑门的构建方法，其特征在于：利用python中的lp工具pulp求解所述寻优模型。

4.如权利要求1所述的受限玻尔兹曼机形式的可逆逻辑门的构建方法，其特征在于：隐藏层节点数n与可见层节点数m的关系为：n≤m-1。

5.如权利要求1所述的受限玻尔兹曼机形式的可逆逻辑门的构建方法，其特征在于：所述受限玻尔兹曼机各节点的神经元的激活函数为取值从-1到1的双曲正切函数。

6.如权利要求5所述的受限玻尔兹曼机形式的可逆逻辑门的构建方法，其特征在于：所述受限玻尔兹曼机各节点的神经元的激活函数为tanh函数。

7.如权利要求6所述的受限玻尔兹曼机形式的可逆逻辑门的构建方法，其特征在于：所述受限玻尔兹曼机各节点的神经元由自旋电子器件构成。

8.如权利要求1所述的受限玻尔兹曼机形式的可逆逻辑门的构建方法，其特征在于：给定的偏置取值范围为整数-4～+4，给定的权重取值范围为整数-4～+4。

9.一种电子设备，包括存储器和处理器，所述存储器存储有计算机程序，其特征在于，所述处理器执行所述计算机程序时实现如权利要求1至8中任一项所述的方法的步骤。

10.一种计算机可读存储介质，其上存储有计算机程序，其特征在于，所述计算机程序被处理器执行时实现如权利要求1至8中任一项所述的方法的步骤。

技术总结本申请属于可逆逻辑门设计相关技术领域，其公开了一种受限玻尔兹曼机形式的可逆逻辑门的构建方法，包括：根据可逆逻辑门的逻辑函数确定受限玻尔兹曼机的节点数；确定可见层节点二进制取值组合对应的状态，若满足可逆逻辑门的逻辑，则为有效，否则为无效；将各节点的二进制取值转换为双极格式之后，构建可逆逻辑门整个系统的能量函数，构成寻优模型，若状态为有效，整个可逆逻辑门系统能量为E<subgt;min</subgt;，若状态为无效，系统能量大于等于E<subgt;min</subgt;+d；以能量差值d最大为目标求解寻优模型，得到可逆逻辑门的偏置矩阵B和权重矩阵W。以上方法通过计算直接确定受限玻尔兹曼机模型参数，无需进行训练，因此，可以快速确定参数且不会出现学习可能陷入局部最优的问题。技术研发人员：游龙,王楷元,段威,曹真受保护的技术使用者：华中科技大学技术研发日：技术公布日：2024/7/29