一种基于数据驱动技术的IPT系统恒压输出控制器构建方法

本发明涉及无线电能传输，具体涉及一种基于数据驱动技术的ipt系统恒压输出控制器构建方法。

背景技术：

1、ipt(磁耦合式电能传输，inductive power transfer)利用高频磁场实现电能的非接触式传输。相较于拔插式电能传输方式，非接触传输方式有效地避免了开关动作时产生的电弧和损耗，进而提高用电设备的安全性和使用寿命。此外，ipt技术提供了灵活、美观的取电方式，解决了家用设备排线杂乱的问题。基于上述优点，该系统在电动汽车、家用设备和植入式医疗器械方面得到了广泛的应用，具有巨大的实际应用价值。

2、考虑到ipt系统正常工作中不可避免地受到参数摄动的影响，如在电池充电过程中电池电阻参数往往是变化的，线圈之间的相对位置不固定导致的耦合系数的变化。这些因素直接导致ipt系统输出产生波动。因此，设计在参数摄动下维持ipt系统恒定输出的控制器是十分重要的。

3、为设计控制器，主流的方法需要建立ipt系统的输入输出数学模型。考虑到ipt系统中存在较多的电感和电容，基于电路原理的建模方法导致建立的系统模型具有较高的系统阶次和非线性因素。而ipt系统大多要求工作在谐振频率附近，系统的输入输出特性与低阶系统输入输出特性相似。因此，基于数据驱动的控制器设计方法提供了一种较为简便设计方法。并且实际应用中对于闭环系统的超调量，收敛速度等暂态性能需要一定的约束，我们在设计控制器时应考虑这些约束。

技术实现思路

1、本发明要解决的技术问题是如何维持ipt系统在参数摄动下的恒压输出并优化系统的暂态性能，提供一种基于数据驱动技术的ipt系统恒压输出控制器构建方法。

2、本发明通过下述技术方案来解决上述技术问题：

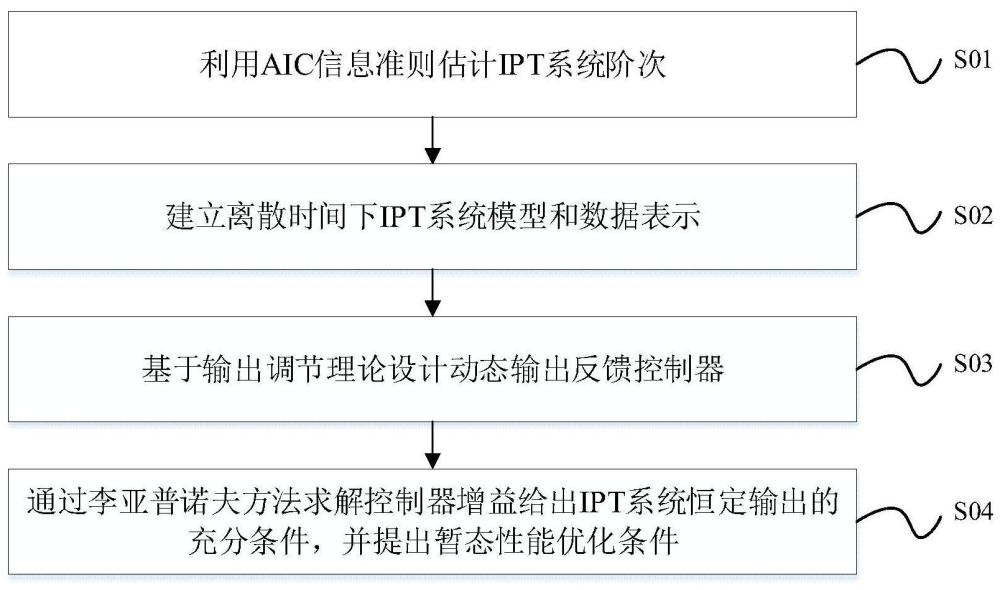
3、一种基于数据驱动技术的ipt系统恒压输出控制器构建方法，所述控制器构建方法包括：

4、结合aic信息准则估计ipt系统的阶次信息；

5、建立离散时间下ipt系统模型和数据表示；

6、基于输出调节理论设计动态输出反馈控制器；

7、通过李亚普诺夫方法求解控制器增益给出所述离散时间下ipt系统模型和数据表示恒定输出的充分条件，并提出暂态性能优化条件。

8、较佳地，所述控制器设计过程不需要先验了解系统阶次：

9、不同阶次下的aic值可由公式(1)确定：

10、vaic(n)＝nen(m(1+ln2π)+ln|∑n|)+2δnmn (1)

11、其中，nen为数据容量，n，m，mn，δn分别为系统阶次，输入维度，未知参数的数量，与nen相关的校正系数，具体参数表达式为：

12、

13、

14、

15、其中，y(k)代表实际测量输出，代表参数模型的输出。最优的系统阶次可由最小的aic值确定，避免了繁琐的阶次估计问题。

16、较佳地，所述离散时间下ipt系统模型和数据表示，包括：

17、根据子空间辨识方法建立所述离散时间下ipt系统模型并通过相似变换得到了简洁的状态空间方程描述；

18、ipt系统的数学模型可由子空间方法辨识得到，我们收集ipt系统的输入输出电压数据。之后，我们对收集到的数据进行qr分解

19、

20、其中，l11，l22是下三角矩阵，是正交阵。

21、根据ipt系统基于数据表示的状态空间方程的和输入输出数据的qr分解，我们得到

22、

23、在上述公式中右乘得到：

24、

25、对l22进行svd分解，我们得到：

26、

27、和拓展的能观性矩阵可选择为：

28、

29、之后，我们可以计算得到系统矩阵和输出矩阵

30、

31、其中，为的右逆。

32、接下来，我们估计和由于和我们在公式(5)两端左乘右乘得到：

33、

34、注意到公式(10)是一个关于参数矩阵和的超定方程，其解可由最小二乘方法得到。至此，我们得到了离散时间下ipt系统的数学模型。为了得到简洁的数学模型表达式，我们引入下列相似变换矩阵：

35、

36、其中，ai，i＝1，2，…，n-1是矩阵的特征多项式的系数，满足

37、zn+a1zn-1+…+an＝0。

38、通过相似变换矩阵(11)，我们得到了系统的伴随标准型矩阵：

39、

40、其中，xc(k)为辨识系统的状态，和为辨识系统参数矩阵，且满足如下关系：

41、

42、

43、上述基于子空间辨识过程可总结为算法1。至此，我们得到所述离散时间下ipt系统模型。

44、

45、根据奇偶向量构建所述离散时间下ipt系统的数据表示，具体为：

46、考虑ipt系统的基于数据表示的状态空间方程，对下列的输入输出数据进行qr分解：

47、

48、其中，称为历史数据，r11，r22，r33为下三角矩阵，q1，q2，q3为正交阵。

49、

50、

51、根据算法2得到的奇偶向量，我们可以构建如下数据驱动无差拍观测器：

52、

53、其中，z(k)为状态x(k)的估计，

54、

55、

56、

57、注意到我们称这一性质为无差拍性质，这意味着观测器状态在有限步内收敛至实际系统的状态。

58、至此，根据所述的数据驱动观测器，我们将输入输出数据转换为输入状态数据，得到了所述离散时间下ipt系统的数据表示。

59、z(k+1)＝z1，tgkz(k)， (15)

60、其中，gk满足：

61、

62、较佳地，通过李亚普诺夫方法求解控制器增益给出ipt系统恒定输出的充分条件，并提出暂态性能优化条件，包括：

63、基于所述离散时间下ipt系统模型，通过李亚普诺夫方法求解控制器增益给出实现ipt系统恒定输出的充分条件可由定理1求解得到：

64、定理1：给定参数矩阵qξ，r和系统模型如果存在矩阵w＞0和适当维数矩阵x和y为下列最小化问题的解：

65、

66、满足：

67、

68、

69、其中，trace{…}代表方阵的迹，代表单位阵，增广系统其参数为：

70、

71、控制器增益可由求解得到。

72、基于所述离散时间下ipt系统的数据表示，通过李亚普诺夫方法求解控制器增益给出实现所述离散时间下ipt系统的数据表示恒定输出的充分条件可由定理2得到：

73、定理2：给定参数矩阵qξ，r和数据表示x0，t，x1，t，如果存在适当维数矩阵和x为下列最小化问题的解:

74、

75、满足

76、

77、

78、其中，z0，t为包含观测器状态z(k)和误差的和项的数据序列。那么，控制器增益可由k＝u0，tq(z0，tq)-1求解得到。

79、类似的，为了优化系统的暂态性能，我们引入如下不等式约束闭环系统的极点分布：

80、

81、其中，表示矩阵的kronecker积。求解引入约束条件(22)后的定理2，我们得到控制器增益klmi＝u0，tq(z0，tq)-1。

82、在所述李亚普诺夫方法求解控制器增益给出ipt系统恒定输出的充分条件的基础上提出暂态性能优化条件：

83、进一步，为了优化闭环系统的暂态性能如收敛速度、阻尼比，我们引入lmi区域约束闭环系统的极点分布。考虑z平面中的椭圆区域：

84、

85、其中，矩阵是hermitian矩阵，lmi区域的形状参数为：

86、

87、xe为椭圆的中心，μ1>0为椭圆的长半轴，μ2>0为短半轴。

88、对于闭环系统acl＝a+bk的全部特征根位于lmi区域中，当且仅当，存在对称正定矩阵p＞0满足：

89、

90、其中，表示矩阵的kronecker积。

91、较佳地，输出调节理论设计动态输出反馈控制器可保证闭环系统在参数摄动实现所述ipt系统的恒压输出的控制目标。

92、我们构造如公式(16)所示的动态输出反馈控制器。

93、

94、其中，g1＝diag{ao，mi}，k为待设计的参数矩阵。基于输出调节理论，我们引入误差的和项以实现对恒定参考信号的跟踪和对参数摄动的抑制。因此，我们选择mi＝1，ni＝1。我们还需要设计观测器增益lo使得系统ao-loc为schur稳定和控制器增益k镇定如下形式的增广系统：

95、

96、基于输出调节理论，如果控制器(16)中观测器增益lo使得系统ao-loc为schur稳定和控制器增益k镇定增广系统(17)，那么该控制器可实现对原系统中恒定参考信号的误差跟踪和抑制参数摄动。一般地，为了实现观测器快速准确地估计系统状态，我们可以基于极点配置的方法设计观测器增益lo，将观测器ao-loc的极点配置到原点。而镇定控制增益可使用李亚普诺夫方法求解得到。

97、本发明的积极进步效果在于：本发明提出的基于数据驱动技术的ipt系统恒压输出控制器构建方法考虑了在模型阶次和参数未知的情况下建立离散时间下的系统模型和控制器设计，同时所设计控制器实现在参数摄动和暂态性能约束情况下的恒压输出，显著提高了ipt系统的鲁棒性和恒压输出跟踪性能，而且所设计控制器可直接部署在单片机中，避免了控制器离散化导致的性能下降。