一种格基层次型全同态数字签名方法及装置

本发明涉及信息安全与密码，特别是指一种格基层次型全同态数字签名方法及装置。

背景技术：

1、随着量子计算机的应用与发展，传统基于大整数分解、离散对数、椭圆曲线等数学问题的公钥密码算法将面临更具有威胁的量子计算攻击，为对抗量子计算对信息安全的影响，新一代具有抵抗量子计算攻击能力的后量子密码算法的研究及优化工作迫在眉睫。

2、2022年7月，美国国家标准与技术研究院发布了第一批标准化的后量子密码算法，第一批被标准化的算法中包括一种公钥加密算法crystals-kyber和三种数字签名算法、crystals-dilithium、falcon、sphincs+。其中falcon是具备实用化潜力的格基签名方案，falcon底层基于数论研究单元格上的环上小整数解困难问题和gpv架构，通过使用快速傅里叶采样算法提升签名方案的效率。

3、现有的围绕falcon后量子签名算法的应用主要集中在算法本身的优化以及在ca和区块链中的应用，结合同态签名算法的改进与应用暂时还没有。

4、现有的层次型全同态签名算法多为基于标准格上的同态签名算法，研究重点多围绕同态运算的设计，关于签名部分的设计较为简单且多停留于理论设计层面，缺乏实际实现与效率分析。

技术实现思路

1、为了解决现有技术存在的层次型全同态签名算法的签名部分的设计较为简单，且多停留于理论设计层面，实现与应用较为困难问题，本发明实施例提供了一种格基层次型全同态数字签名方法及装置。所述技术方案如下：

2、一方面，提供了一种格基层次型全同态数字签名方法，该方法通过格基层次型全同态数字签名装置实现，方法包括：

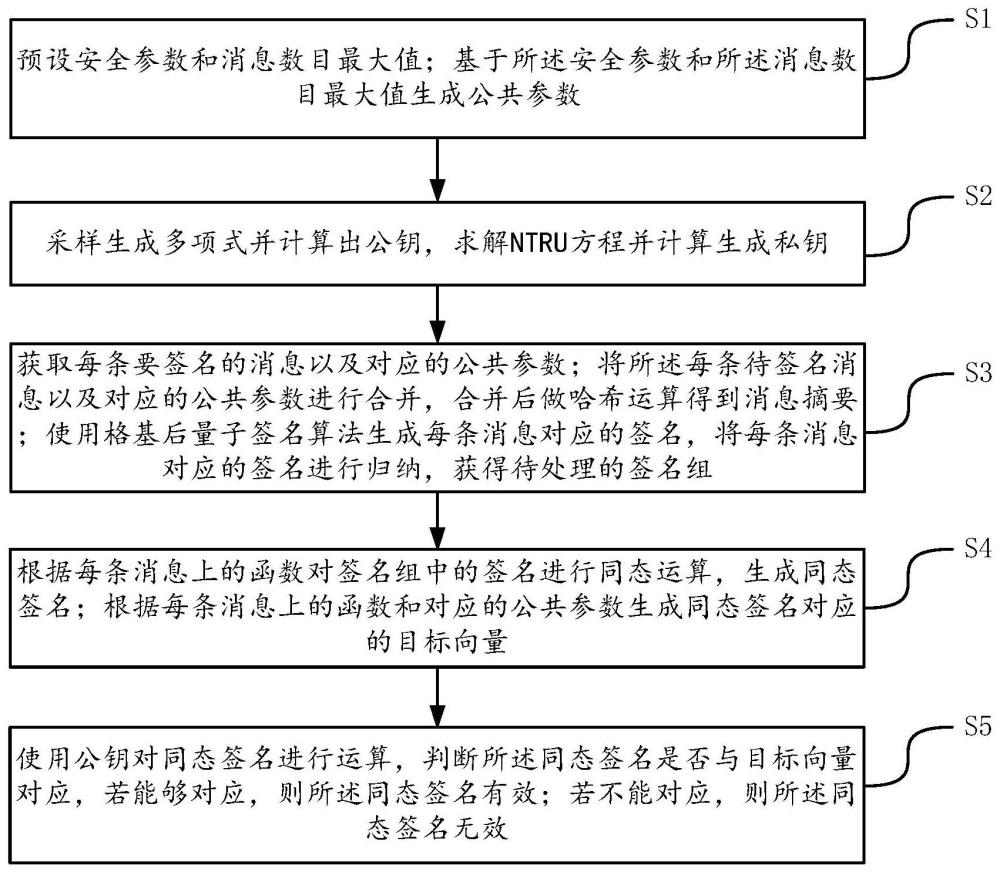
3、s1、预设安全参数和消息数目最大值；基于安全参数和消息数目最大值生成公共参数；

4、s2、采样生成多项式并计算出公钥，求解ntru方程并计算生成私钥；

5、s3、获取每条要签名的消息以及对应的公共参数；将每条待签名消息以及对应的公共参数进行合并，合并后做哈希运算得到消息摘要；使用格基后量子签名算法生成每条消息对应的签名，将每条消息对应的签名进行归纳，获得待处理的签名组；

6、s4、根据每条消息空间上的函数对签名组中的签名进行同态运算，生成同态签名；根据每条消息上的函数和对应的公共参数生成同态签名对应的目标向量；

7、s5、使用公钥对同态签名进行运算，判断同态签名是否与目标向量对应，若能够对应，则同态签名有效；若不能对应，则同态签名无效。

8、可选地，s1中，预设安全参数和消息数目最大值；基于安全参数和消息数目最大值生成公共参数，包括：

9、预设安全参数和消息数目最大值n；

10、根据安全参数和消息数目最大值n，以每个参数ri对应的消息mi或序号i为种子，通过高斯采样输出公共参数r1，r2…rn，将公共参数ri作为盐值与消息mi混合后，将混合后的数值经哈希函数运算，生成环上小整数解问题的目标向量；

11、其中，公共参数的数目与消息数目最大值n一致。

12、可选地，s2中，采样生成多项式并计算出公钥，求解ntru方程并计算生成私钥，包括：

13、构建一元n次不可约多项式φ＝xn+1和模数q，从整数上的离散高斯分布中采样n次多项式f，g，其中，多项式f，g为随机的n次多项式，多项式f满足模q可逆，且多项式g和-f的范数满足：

14、

15、基于多项式f和多项式g，求解ntru方程得到多项式f,g，对f，g，f，g做快速傅里叶变换后组合获得二元矩阵b；

16、基于二元矩阵b，使用快速傅里叶采样算法得到falcon树t；私钥sk由b和t两部分组成；将多项式g和f的逆相乘并模q得到公钥pk的值h。

17、可选地，s3中，获取每条要签名的消息以及对应的公共参数；将每条待签名消息以及对应的公共参数进行合并，合并后做哈希运算得到消息摘要；使用格基后量子签名算法生成每条消息对应的签名，将每条消息对应的签名进行归纳，获得待处理的签名组，包括：

18、输入消息m1，m2，…mi…，mn，私钥sk，系统参数r1，r2，…ri…，rn以及最大签名平方范数；

19、将公共参数中的盐值ri和消息mi组合成串，经哈希函数处理后生成环上小整数解困难问题的目标向量vi；将vi转换为fft的形式，并与私钥中的矩阵b的逆相乘得到ti；

20、将ti和私钥中的falcon树t输入快速傅里叶采样算法得到zi，将ti和zi的差与私钥中的矩阵b相乘得到签名值的fft形式si；

21、检验签名值si的平方范数是否小于等于输入的最大签名平方范数，若不满足，则返回重新进行采样；若满足，则对si做fft逆变换，得到签名向量si1和si2；

22、判断签名向量si1和si2能否验证通过，若不能，则重新采样；若验证通过，则取si2进行压缩编码得到签名值si；循环操作n次获得待处理签名组。

23、可选地，s4中，根据每条消息上的函数对签名组中的签名进行同态运算，生成同态签名；根据每条消息上的函数和对应的公共参数生成同态签名对应的目标向量，包括：

24、输入消息空间上的函数e，消息m1，m2，…mi…，mn，签名s1,s2,…si…,sn以及系统参数r1，r2，…ri…，rn；

25、对每个签名si进行解压缩处理得到si1和si2，通过哈希函数计算si的目标向量值vi；

26、将函数e分解为基本运算的组合表达：e1，e2…ei，…en；其中，基本运算的组合包括：加法、乘法和数乘的组合；

27、分别读取每个基本运算ei，以及对应的消息所对应的签名值和目标向量值；将签名值和目标向量值输入对应的基本同态运算算法，生成新的签名值和目标向量值并保存，作为下一次运算的输入；

28、循环操作直到完成所有运算操作，对得到的签名值进行压缩编码，输出同态签名值se和对应的目标向量值ve。

29、可选地，s4中，当基本运算e(m1,m2)＝m1+m2时，包括：

30、对于消息空间上的基本运算函数e，对m1,m2的签名s1,s2进行同态运算s1+s2得到同态签名，对s1,s2对应的目标向量v1,v2进行同态运算v1+v2得到同态签名对应的目标向量。

31、可选地，s4中，当基本运算e(m1,m2)＝m1·m2时，包括：

32、对于消息空间上的基本运算函数e，对m1,m2的签名s1,s2进行同态运算s1·v2得到同态签名，对s1,s2对应的目标向量v1,v2进行同态运算v1·v2得到同态签名对应的目标向量。

33、可选地，s4中，当基本运算e(m1)＝c·m1时，包括：

34、对于消息空间上的基本运算函数e，对m1的签名s1进行同态运算c·s1得到同态签名，对s1对应的目标向量v1进行同态运算c·v1得到同态签名对应的目标向量，其中c为常数。

35、可选地，s5中，使用公钥对同态签名进行运算，判断同态签名是否与目标向量对应，若能够对应，则同态签名有效；若不能对应，则同态签名无效，包括：

36、输入同态签名se，以及对应的目标向量ve和公钥pk；

37、解压缩同态签名se得到se1，se2，判断se1，se2的大小是否在-q/2和q/2之间，若不满足则对se1，se2进行模q处理，使其每个系数都在-q/2和q/2范围内；若满足，判断se1，se2是否满足se1+se2h＝vemod(φ,q)，若满足，则验证通过，否则验证不通过。

38、另一方面，提供了一种格基层次型全同态数字签名装置，该装置应用于格基层次型全同态数字签名方法，该装置包括：

39、参数生成模块，用于预设安全参数和消息数目最大值；基于安全参数和消息数目最大值生成公共参数；

40、密钥计算模块，用于采样生成多项式并计算出公钥，求解ntru方程并计算生成私钥；

41、签名生成模块，用于获取每条要签名的消息以及对应的公共参数；将每条待签名消息以及对应的公共参数进行合并，合并后做哈希运算得到消息摘要；使用格基后量子签名算法生成每条消息对应的签名，将每条消息对应的签名进行归纳，获得待处理的签名组；

42、同态运算模块，用于根据每条消息空间上的函数对签名组中的签名进行同态运算，生成同态签名；根据每条消息上的函数和对应的公共参数生成同态签名对应的目标向量；

43、签名验证模块，用于使用公钥对同态签名进行运算，判断同态签名是否与目标向量对应，若能够对应，则同态签名有效；若不能对应，则同态签名无效。

44、另一方面，提供一种格基层次型全同态数字签名设备，所述格基层次型全同态数字签名设备包括：处理器；存储器，所述存储器上存储有计算机可读指令，所述计算机可读指令被所述处理器执行时，实现如上述格基层次型全同态数字签名方法中的任一项方法。

45、另一方面，提供了一种计算机可读存储介质，所述存储介质中存储有至少一条指令，所述至少一条指令由处理器加载并执行以实现上述格基层次型全同态数字签名方法中的任一项方法。

46、本发明实施例提供的技术方案带来的有益效果至少包括：

47、本发明提供的方法和装置采用falcon算法构造单个消息的签名方案，该签名方案的安全性依赖falcon的安全性，具有十分可靠的后量子安全保证，填补了现行国产商用数字签名算法不可抗量子的空缺。

48、结合实用化的格基签名算法，基于gpv架构设计了基本同态运算算法，本发明缩短了进行一次同态乘法运算所需时间，且生成的同态签名长度与单个签名长度相近，进而提升了层次型全同态签名方案的效率。

49、在安全性方面，本发明基于数论研究单元格上的环上小整数解困难问题，而非标准格上的其他困难问题，安全证明更加简明，提升了方案的安全性。

50、本发明基于实用化的格基签名方案，由此构造的签名方案，不仅拓宽了格基签名算法的应用领域，且使得本方案具有良好的兼容性与适用性，能部署于各种资源受限的软硬件平台，具有广泛的应用领域。