一种多谐振体组合结构低频宽带抑振方法与流程

本发明涉及水下结构低频振动噪声控制，尤其涉及一种多谐振体组合结构低频宽带抑振方法。

背景技术：

1、低频振动噪声由于波长较长，常规控制手段效果不佳，一直是振动噪声控制领域的难点问题，基于局域共振机理的周期结构具有弹性波带隙，其带隙的产生取决于谐振体共振特性与基体中弯曲波的相互作用，因而带隙频率与谐振体的共振频率密切相关，可在低频形成带隙，从而为低频振动噪声控制提供了新的技术途径，但目前针对水下结构的设计较少。

2、公开号为cn106678271a的一种局域共振低频带隙抑振周期结构，包括包括周期分布的质量元件、弹性元件和基体；周期单元包括金属结构即质量元件，质量元件侧面包围一圈橡胶或硅胶材料环状结构即弹性元件，质量元件周向侧面为带有一定形状的曲面，并且弹性元件与质量元件之间相互贴合，然后将弹性元件包围质量元件作为整体周期排列在弹性结构基体中，其中弹性元件与基体之间也是相互贴合的。

3、但现有技术中在相对较小的附加质量比条件下，局域共振周期结构普遍存在“带隙过窄”的问题，再加上水下环境中流体附加质量的影响，使得在较低频率范围内很难获得较宽的抑振频带，多谐振体组合型局域共振周期结构可在一定程度上改善这一情况，但效果比较有限，当胞元内的谐振体数量增加时，带隙数量也会相应增加，但这并不能保证抑振频带的拓宽，主要是带隙数量虽然增加了，但单个带隙的宽度往往会变窄，使得总的带隙宽度增加不如预期，其次，多个带隙在频域上往往是离散分布的，使得所获得的振动衰减区域也是离散的，并不能获得真正意义上的宽频抑振效果，此外，多组谐振体或多自由度谐振体的频率如何组合并无一定之规，设计人员往往根据被控结构的模态特性与工程经验确定，因而并不能充分发挥多组谐振体或多自由度谐振体局域共振结构的宽带抑振优势，这使得目前的局域共振周期结构无法兼顾低频和宽频抑振效果，难以满足实际工程中的减振需求。

技术实现思路

1、有鉴于此，本发明提出了一种多谐振体组合结构低频宽带抑振方法，用于实现局域共振结构的灵活设计并在兼顾低频特性的基础上大幅拓宽抑振频带。

2、本发明的技术方案是这样实现的：本发明提供了一种多谐振体组合结构低频宽带抑振方法，其特征在于，包括以下步骤：

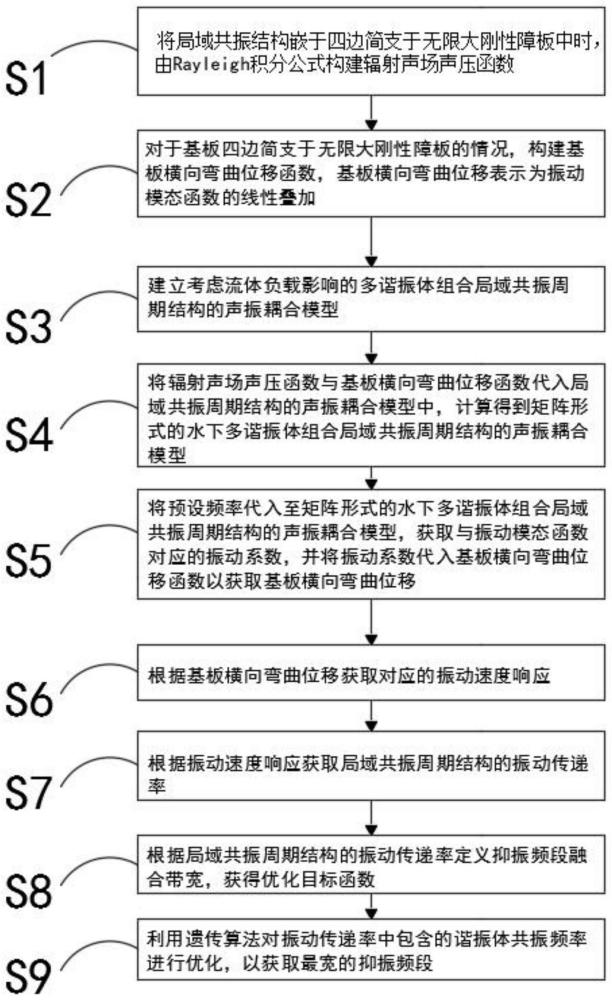
3、s1，将局域共振结构嵌于四边简支于无限大刚性障板中时，由rayleigh积分公式构建辐射声场声压函数；

4、s2，对于基板四边简支于无限大刚性障板的情况，构建基板横向弯曲位移函数，基板横向弯曲位移表示为振动模态函数的线性叠加；

5、s3，建立考虑流体负载影响的多谐振体组合局域共振周期结构的声振耦合模型；

6、s4，将辐射声场声压函数与基板横向弯曲位移函数代入局域共振周期结构的声振耦合模型中，计算得到矩阵形式的水下多谐振体组合局域共振周期结构的声振耦合模型；

7、s5，将预设频率代入至矩阵形式的水下多谐振体组合局域共振周期结构的声振耦合模型，获取与振动模态函数对应的振动系数，并将振动系数代入基板横向弯曲位移函数以获取基板横向弯曲位移；

8、s6，根据基板横向弯曲位移获取对应的振动速度响应；

9、s7，根据振动速度响应获取局域共振周期结构的振动传递率；

10、s8，根据局域共振周期结构的振动传递率定义抑振频段融合带宽，获得优化目标函数；

11、s9，利用遗传算法对振动传递率中包含的谐振体共振频率进行优化，以获取最宽的抑振频段。

12、在以上技术方案的基础上，优选的，所述步骤s1中将局域共振结构嵌于四边简支于无限大刚性障板中时，由rayleigh积分公式构建辐射声场声压函数，表达式为：

13、

14、式中，为基板表面振速；ω为角频率；ρf为水的密度，r表示场点、r′＝(x′，y′，z′)到基板表面一点r＝(x，y，0)的距离，a为基板的长度，b为基板的宽度，k为波数，x和y分别为基板上的位置坐标，j为虚数单位。

15、在以上技术方案的基础上，优选的，所述步骤s2中对于基板四边简支于无限大刚性障板的情况，构建基板横向弯曲位移函数，基板横向弯曲位移w(x，y)表示为振动模态函数的线性叠加，表达式为：

16、

17、其中，wmn为(m，n)阶振动模态函数；amn为振动模态函数对应的振动系数；其(m，n)阶振动模态函数的表达式为：

18、wmn(x，y)＝sin(kmx)sin(kny)；

19、式中，km＝mπ/a；kn＝nπ/b，其中，a为基板的长度，b为基板的宽度。

20、在以上技术方案的基础上，优选的，所述步骤s3中建立考虑流体负载影响的多谐振体组合局域共振周期结构的声振耦合模型，表达式为：

21、

22、其中，dp为基板弯曲刚度，其表达式为：dp＝ephp3/12(1-νp2)；式中，ep为基板的杨氏模量，vp为基板的泊松比；的表达式为：ω为角频率；ρp为基板的密度；hp为基板的厚度；w(r)为基板横向弯曲位移；f0为作用在基板(x0,y0)位置处的简谐点力；p(x，y，0)为基板表面声压；fs为各谐振体对基板的反作用力，表达式为：对于单自由度谐振体zfs＝ω2msks/(ks-ω2ms)，其中ms为胞元内第s个谐振体的质量，ks为胞元内第s个谐振体的刚度；rt＝（xt，yt)表示由原点指向第t个胞元中心点的向量，代表了胞元的位置，rs＝(f1s,r2s)表示由胞元中心点指向胞元内第s个谐振体的向量，代表了胞元内谐振体的相对位置。

23、在以上技术方案的基础上，优选的，所述步骤s4中将辐射声场声压函数与基板横向弯曲位移函数代入局域共振周期结构的声振耦合模型后，再将无穷级数进行截断，并利用正余弦函数积分正交性进行化简，最终计算得到矩阵形式的水下多谐振体组合局域共振周期结构的声振耦合模型。

24、在以上技术方案的基础上，优选的，所述步骤s4中的矩阵形式的水下多谐振体组合局域共振周期结构的声振耦合模型，表达为：

25、(k+jωz-ω2m-fa)a＝f；

26、式中，矩阵k、m、z、f中的元素分别为：

27、

28、矩阵fa表示为：

29、

30、其中，矩阵w中元素为：

31、wsti，1＝sin(km(xt+r1s))sin(kn(yt+r2s))。

32、在以上技术方案的基础上，优选的，所述步骤s6中根据基板位移获取对应的振动速度响应，其中，计算表达式为：

33、v＝jω*w；

34、式中，v为振动速度响应，ω为角频率，w为基板横向弯曲位移。

35、在以上技术方案的基础上，优选的，所述步骤s7中根据振动速度响应获取局域共振周期结构的振动传递率，其中，还包括以下步骤：

36、s71，选取基板上若干个点位置，分别提取各点位置的振动响应；

37、s72，根据振动速度响应和振动传递函数计算局域共振周期结构的振动传递率；

38、其中，振动传递函数的表达式为：

39、

40、式中，vf为激励点的速度响应，vri为所选取传递路径上的各点速度响应。

41、在以上技术方案的基础上，优选的，所述步骤s8中根据局域共振周期结构的振动传递率定义抑振频段融合带宽，获得优化目标函数，其中，定义表达式为：

42、bwm＝max(ω)，{tl(ω)＜0，fs∈ω}；

43、式中，bwm为优化目标函数，ω为振动传递率tl＜0的频率范围，在局域共振结构的振动传递率曲线中，包含所有谐振体的共振频率，tl＜0的最大频率范围，即为抑振频段融合带宽。

44、在以上技术方案的基础上，优选的，所述步骤s9中利用遗传算法对振动传递率中包含的谐振体共振频率进行优化，以获取最宽的抑振频段，其中，以谐振体的质量、刚度为遗传算法优化变量，以质量占比为约束条件，以抑振频段的最大宽度bwm和抑振频段内的振动衰减量最大值为目标函数进行多目标优化，最后求得一组最佳变量，即获得最宽的抑振频段。

45、本发明的多谐振体组合结构低频宽带抑振方法相对于现有技术具有以下有益效果：

46、(1)通过建立考虑流体负载影响的多谐振体组合局域共振周期结构的声振耦合模型，将辐射声场声压函数与基板横向弯曲位移函数代入局域共振周期结构的声振耦合模型中，计算得到矩阵形式的水下多谐振体组合局域共振周期结构的声振耦合模型，将预设频率代入到矩阵形式的水下多谐振体组合局域共振周期结构的声振耦合模型中，并通过基板横向弯曲位移函数获得基板的横向弯曲位移，进而可获得局域共振周期结构板的振动传递率，并定义抑振频段融合带宽，可保证抑振频带的拓宽，能够获得真正意义上的宽频抑振效果，并使得多组谐振体或多自由度谐振体的频率组合效果提升，充分发挥多组谐振体或多自由度谐振体局域共振结构的宽带抑振优势；

47、(2)通过定义抑振频段融合带宽，获得优化目标函数后，利用遗传算法对振子的共振频率进行优化，以获得最宽的抑振频段，实现局域共振结构的灵活设计并在兼顾低频特性的基础上大幅拓宽抑振频带，满足实际工程中的减振需求。