一种偏安全型大坝安全监测数据分段统计模型构建方法与流程

本发明涉及大坝运行安全监测与管理，特别是一种偏安全型大坝安全监测数据分段统计模型构建方法。

背景技术：

1、大坝是水利工程建设的核心之一，是提高水资源调控和配置的重要工程。为保证大坝安全运行，相关变形监测理论和方法备受关注，其中，各类大坝变形预测模型通过挖掘外界因素和变形测值的内在联系，反映大坝安全运行状态，成为研究大坝变形的重要手段，为大坝安全运行期间的安全管理提供重要技术支持。

2、对于大坝安全监测数据，由于统计模型执行速度快，输入变量和相应变量间有高度相关性，统计模型得到广泛应用。进行统计模型的构建，进而对大坝安全性态进行评估、分析、诊断、预测、预警，是发挥大坝安全监测数据价值的重要途径之一。随着各种新理论和新思路新方法的出现，大坝变形监测模型的精度不断提高。智能算法和统计模型结合，能够对大坝变形监测序列等非线性时间序列有更好的预测效果。

3、但由于大坝自身结构受外界因素影响，会产生复杂的动态变化，因此监测模型的精度会随着时间的延长而减弱，同时由于平方损失函数的数学特性表现良好，最小二乘回归模型等一系列方法被用来进行大坝安全监测模型的建立，但该种方法只能提供平均状况的数据信息，对于数据本身的极值变化情况无法解决。

技术实现思路

1、本发明的目的在于克服上述不足，提供一种偏安全型大坝安全监测数据分段统计模型构建方法，旨在考虑大坝安全监测数据特征值的相对重要性，反映数据本身特征值在建立模型中的重要程度，并在线识别大坝自身结构性态的变化，对大坝安全监测数据进行分割，进而构建和估计偏安全型大坝安全监测数据分段统计模型。

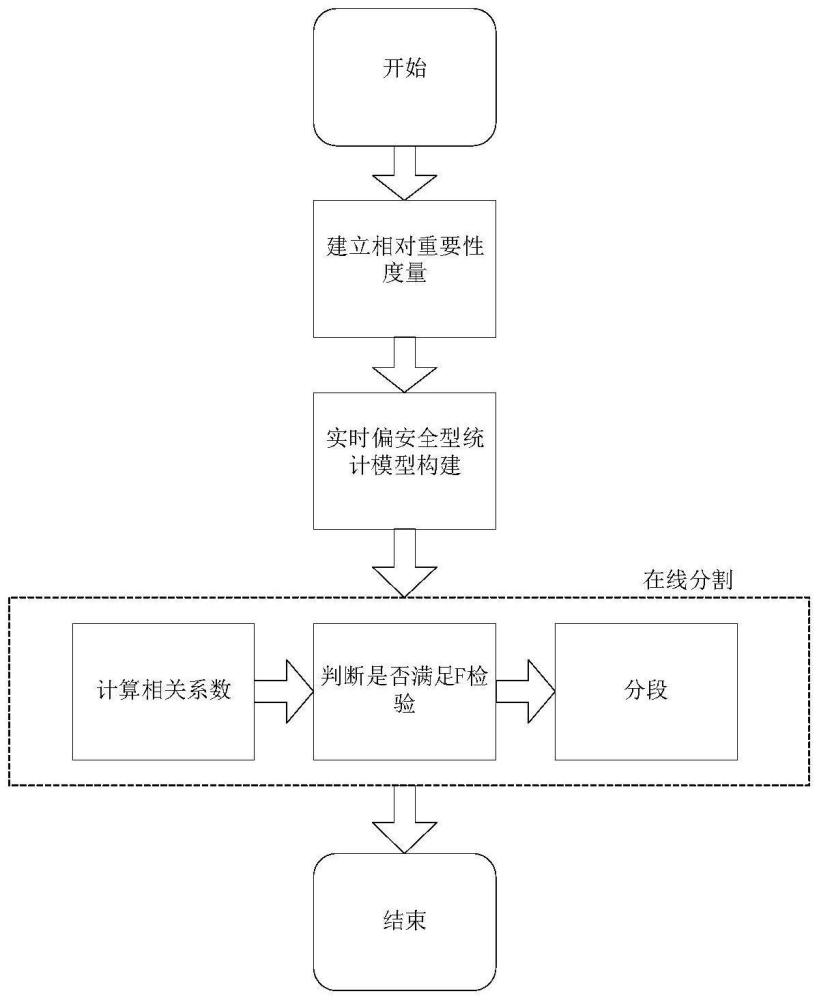
2、为解决上述技术问题，本发明所采用的技术方案是：一种偏安全型大坝安全监测数据分段统计模型构建方法，它包括如下步骤：

3、s1、在分析大坝安全监测数据特性的基础上，考虑大坝安全监测数据与大坝安全的关系，建立大坝安全监测数据的相对重要性度量，衡量监测数据映射的大坝安全状态；

4、s2、将大坝安全监测数据的相对重要性度量归一化后，借鉴加权最小二乘法原理，将其作为权重因子，构建偏安全型统计模型；

5、s3、采用pearson相关系数衡量偏安全统计模型的准确性，并通过在线分割算法动态识别大坝自身结构性态变化，对大坝安全监测数据序列进行在线分割，实时发现和预测大坝变形特性。

6、进一步地，所述步骤s1中建立大坝安全监测数据的相对重要性度量，其构建方法如下：

7、将大坝安全监测数据作为一组时间序列，记为yn,n＝1,2,…,n，在某一时间范围内，监测数据围绕其均值μn进行波动变化，构建的监测数据相对重要性度量指标mi(yn)表示为：

8、mi(yn)＝|yn-μn|p,n＝1,2,…,n (1)

9、式中，mi(yn)为监测数据yn所对应的相对重要性，yn为第n个监测数据，μn为监测数据yn所对应的均值，n为监测数据总的个数，p为相对重要性指数，取1或2。

10、进一步地，所述步骤s2具体如下：

11、针对大坝安全监测数据的统计模型，以混凝土重力坝变形监测量统计模型建立对应的偏安全型统计模型；

12、混凝土重力坝变形监测数据统计模型，表示为：

13、δ＝δh+δt+δθ+ε (2)

14、式中，δ表示混凝土坝的变形，δh表示变形中的水压分量，δt表示变形中的温度分量，δθ表示变形中的时效分量，ε表示变形误差；

15、只考虑库水压力对混凝土重力坝变形的影响，则：

16、

17、式中，ai表示待估计的系数，h表示水库上游水深；

18、只考虑周期项温度对混凝土重力坝变形的影响，则：

19、

20、式中，t为监测时间对应的天数，b1i和b2i为待估计的系数，m为考虑的每年内变形周期数；

21、考虑线性和对数型时效分量，即：

22、δθ＝c1lnθ+c2θ (5)

23、式中，θ以年为单位，为监测时间相对于监测起始时刻的年数，c1和c2为待估计的系数；

24、将式(2)表示为时间序列的形式，并结合式(1)，则偏安全型大坝安全监测数据统计模型表示为：

25、

26、式中，δn为n时刻的混凝土坝变形，δhn表示n时刻变形中的水压分量，δtn表示n时刻变形中的温度分量，δθn表示n时刻变形中的时效分量，εn表示n时刻变形误差；n为混凝土坝变形时间序列的总个数；μn为监测数据yn所对应的均值，p为相对重要性指数，取1或2；

27、针对式(5)，为了实现该模型的参数估计，将式(6)中的mi(δn)进行归一化处理，记为ωn，将其作为加权最小二乘法中的权重，即：

28、

29、从而，式(6)对应的加权最小二乘估计模型可表示为：

30、

31、式中，δ为监测数据向量，x为水压、温度和时效构成的自变量向量，β为水压、温度和时效分量对应的待估计参数组成的参数向量，ε为误差向量，w为ωn,n＝1,2,…,n构成的权重矩阵，qw(β)为最小二乘估计的代价函数；

32、若x为列满秩阵、w为正定阵，则式(8)中β的估计结果为：

33、β＝(x′wx)-1x′wδ (9)

34、进一步地，所述步骤s3具体如下：

35、设有序列u＝(u1,u2,…,um),且u～n(0,σ)，其中m为序列的总个数，n(0,σ)表示期望为0，标准差为σ的正态分布；令

36、f(1,m)＝t(0,m) (10)

37、表示序列u只分成1段的似然函数；而

38、f(2,m)＝t(1,m-1) (11)

39、表示序列u从m处分为2段的似然函数，其中

40、t(h,m)＝(m-h)lg(s*2) (12)

41、式中s*2表示序列uh+1,uh+2,…,um的样本方差，如果

42、

43、表示u从m处分为2段更合理，其中δ为阈值；

44、在上式中，f服从fα(m,m-1)；当给定显著性水平α时，可以确定fα(m,m-1)的值；

45、偏安全型大坝安全监测数据统计模型在线分割流程如下：

46、(1)给定大坝安全监测序列δ＝(δ1,δ2,…δm)，随着监测序列采集当前时刻数据，建立偏安全型大坝安全监测数据统计模型；

47、(2)计算当前时刻偏安全型大坝安全监测数据统计模型的pearson相关系数，将其作为随时间变化的时间序列u＝(u1,u2,…,um)；

48、(3)分别计算序列u的样本方差其中t＝1,2,…,m-1，计算f(1,m)和f(2,m)；

49、(4)在给定显著性水平的情况下，可以确定阈值δ＝fα(m,m-1)的值，为排除某时刻数据测量误差，当ft+ft+1+ft+2＞3δ时，则从该点进行分段，否则返回步骤(1)。

50、本发明有益效果：相对于现有的预测分析模型，本发明在分析大坝安全监测数据特性的基础上，考虑大坝安全监测数据与大坝安全的关系，对大坝监测数据的相对重要性进行度量，借鉴加权最小二乘法的相关思想和技术，以及在线分割递推算法，构建和估计了偏安全型大坝安全监测数据分段统计分析模型，能够发现和预测大坝自身结构性态在外界因素影响下的时态变化，保留实际监测数据中波动性、包络监测数据中极值、分析结果偏于安全的能力和特征。