一种基于粒子群优化算法的工程问题优化方法

本发明适用于数据处理领域，尤其涉及一种基于粒子群优化算法的工程问题优化方法。

背景技术：

1、自遗传算法被提出以来，计算智能引起了广泛的关注，并成为处理复杂理论和现实生活中优化问题的有效工具。目前，每年都有许多基于种群的随机优化算法涌现。与传统的优化方法相比，基于种群的算法易于实现，并且可以在大多数问题上能提供近似最优解。此外，它们还适用于非连续和不可微分问题。当没有数学模型时，基于种群的算法仍然适用。基于种群的算法为解决np-难问题提供了一种有效的途径。

2、作为一种广泛适用的基于种群的算法，粒子群算法(pso)收敛速度快，可以获得比大多数其他同行算法更好的解。然而现有的粒子群算法普遍存在性能较差且适用范围小的问题。

3、因此亟需一种新的基于粒子群优化算法的工程问题优化方法解决上述技术问题。

技术实现思路

1、本发明提供了一种基于粒子群优化算法的工程问题优化方法，旨在提高现有粒子群优化算法的性能和适应性，以应用于机械制造行业的工程问题优化，降低工程成本。

2、本发明提供了一种基于粒子群优化算法的工程问题优化方法，包括以下步骤：

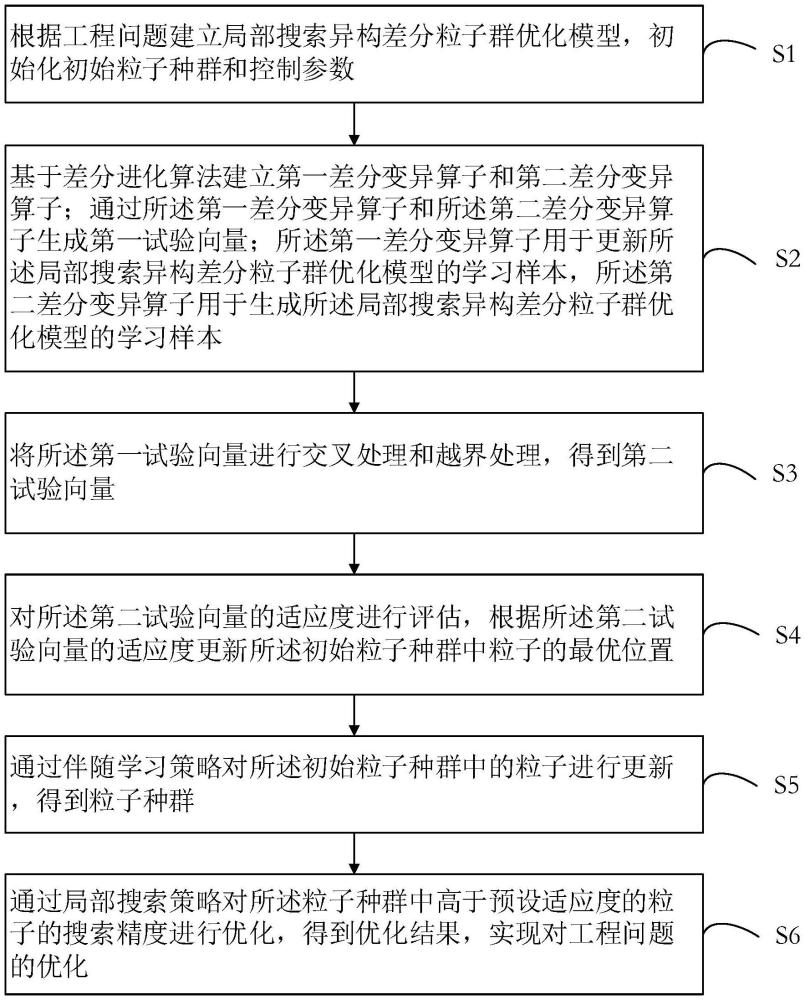
3、s1、根据工程问题建立局部搜索异构差分粒子群优化模型，初始化初始粒子种群和控制参数；

4、s2、基于差分进化算法建立第一差分变异算子和第二差分变异算子；通过所述第一差分变异算子和所述第二差分变异算子生成第一试验向量；所述第一差分变异算子用于更新所述局部搜索异构差分粒子群优化模型的学习样本，所述第二差分变异算子用于生成所述局部搜索异构差分粒子群优化模型的学习样本；

5、s3、将所述第一试验向量进行交叉处理和越界处理，得到第二试验向量；

6、s4、对所述第二试验向量的适应度进行评估，根据所述第二试验向量的适应度更新所述初始粒子种群中粒子的最优位置；

7、s5、通过伴随学习策略对所述初始粒子种群中的粒子进行更新，得到粒子种群；

8、s6、通过局部搜索策略对所述粒子种群中高于预设适应度的粒子的搜索精度进行优化，得到优化结果，实现对工程问题的优化。

9、优选的，定义vi为所述第一试验向量，则所述第一差分变异算子满足以下关系式：

10、vi＝pbestr1+f(pbestr2+epbestr3) (i<ps1)；

11、其中，epbestr3表示从当前粒子种群中随机选择的个体最佳位置，ps1表示所述第一差分变异算子的子种群大小，r1，r2，r3为互斥的随机整数，f表示缩放因子。

12、优选的，所述第二差分变异算子满足以下关系式：

13、vi＝pbesti+f(pbestibest-pbesti)+f(pbestr4-epbestr5)；

14、其中，epbestr5表示从当前粒子种群中随机选择的个体最佳位置，r4和r5为互斥的随机整数。

15、优选的，所述交叉处理满足以下关系式：

16、

17、其中，ui,j表示第i个粒子在第j维变量的试验向量，xi,j表示第i个粒子在第j维变量的目标向量，cri为交叉概率，k为随机维数。

18、优选的，所述越界处理满足以下关系式：

19、ui,j＝(pbesti,j+upj)/2 if ui,j>upj；

20、ui,j＝(pbesti,j+lowj)/2 if ui,j<lowj；

21、其中，pbesti,j表示第i个粒子的个体最佳位置，upj表示第j维变量的上限，lowj表示第j维变量的下限。

22、优选的，所述伴随学习策略为：对所述初始粒子群中的学习粒子随机生成对应的伴随粒子，判断所述学习粒子的适应度是否高于所述伴随粒子，若是则根据预设方法对所述学习粒子进行更新。

23、优选的，所述预设方法为

24、veli,d＝w·veli,d+c·rd(pbesti,d-posi,d)；

25、其中，veli,d表示粒子的速度，w表示惯性权重，c表示加速因子，rd表示取值范围在0到1之间的随机数，posi,d表示第i个粒子的位置，pbesti,d表示i个粒子的个体最佳位置，d表示变量维数的序号。

26、与现有技术相比，本发明通过建立局部搜索异构差分粒子群优化模型，初始化初始粒子种群和控制参数；基于差分进化算法建立第一差分变异算子和第二差分变异算子；通过第一差分变异算子和第二差分变异算子生成第一试验向量；所述第一差分变异算子用于更新所述局部搜索异构差分粒子群优化模型的学习样本，所述第二差分变异算子用于生成所述局部搜索异构差分粒子群优化模型的学习样本；将所述第一试验向量进行交叉处理和越界处理，得到第二试验向量；对所述第二试验向量的适应度进行评估，根据所述第二试验向量的适应度更新所述初始粒子种群中粒子的最优位置；通过伴随学习策略对所述初始粒子种群中的粒子进行更新，得到粒子种群；通过局部搜索策略对所述粒子种群中高于预设适应度的粒子的搜索精度进行优化，得到优化结果，根据优化结果对工程进行优化，本发明提出的方法能广泛应用于机械设计、电力经济调度、化工生产过程优化、控制系统设计等工程优化问题。这样本发明有效提高了粒子群优化算法的性能和适应性，有效提高了对工程问题的优化效率。

技术特征：

1.一种基于粒子群优化算法的工程问题优化方法，其特征在于，包括以下步骤：

2.如权利要求1所述的基于粒子群优化算法的工程问题优化方法，其特征在于，定义vi为所述第一试验向量，则所述第一差分变异算子满足以下关系式：

3.如权利要求2所述的基于粒子群优化算法的工程问题优化方法，其特征在于，所述第二差分变异算子满足以下关系式：

4.如权利要求3所述的基于粒子群优化算法的工程问题优化方法，其特征在于，所述交叉处理满足以下关系式：

5.如权利要求4所述的基于粒子群优化算法的工程问题优化方法，其特征在于，所述越界处理满足以下关系式：

6.如权利要求5所述的基于粒子群优化算法的工程问题优化方法，其特征在于，所述伴随学习策略为：对所述初始粒子群中的学习粒子随机生成对应的伴随粒子，判断所述学习粒子的适应度是否高于所述伴随粒子，若是则根据预设方法对所述学习粒子进行更新。

7.如权利要求6所述的基于粒子群优化算法的工程问题优化方法，其特征在于，所述预设方法为

技术总结本发明适用于数据处理领域，尤其涉及一种基于粒子群优化算法的工程问题优化方法。与现有技术相比，本发明通过建立局部搜索异构差分粒子群优化模型，初始化初始粒子种群和控制参数；通过第一差分变异算子和第二差分变异算子生成第一试验向量；将所述第一试验向量进行交叉处理和越界处理，得到第二试验向量；对所述第二试验向量的适应度进行评估，根据所述第二试验向量的适应度更新所述初始粒子种群中粒子的最优位置；通过伴随学习策略对所述初始粒子种群中的粒子进行更新，得到粒子种群；通过局部搜索策略对所述粒子种群中高于预设适应度的粒子的搜索精度进行优化，得到优化结果。这样本发明有效提高了粒子群优化算法的性能和适应性。技术研发人员：林安平,彭乘风,廖勇,李翔,廖芳芳受保护的技术使用者：湘南学院技术研发日：技术公布日：2024/7/29