一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法

本发明涉及建筑工程和土木工程，具体为一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法。

背景技术：

1、在建筑工程和土木工程中，锚固浅基础是一种广泛应用的结构元素，用于提供对建筑物和其他结构的支撑并确保其稳定性。特别是在黏性土中，基础的抗滑承载力是设计中的一个关键参数。传统的计算方法主要针对无裙板浅基础或有裙板浅基础的抗滑承载力进行设计。传统方法中，极限锚固抗力的计算基于基础与泥面接触面积乘以原状土体不排水抗剪强度。在这些情况下，基础的开孔部分被视为减少了可用于抵抗滑移的有效面积。

2、然而，随着工程需求的演变和对结构效率的追求，新型开孔锚固浅基础被提出以优化结构性能和资源利用。与传统基础不同，新型开孔锚固浅基础的设计采用无顶盖的基础，允许基础整体入土，并与地基土体形成一个整体承载系统。在此系统中，基础开孔部分不再被视为单纯减少承载面积，而是通过入土的栅栏部分与土体共同工作，从而对承载力的减少产生较小影响。

3、现有技术中的计算方法无法准确评估这种新型基础的性能，尤其是在开孔设计方面。传统的有裙板或无裙板浅基础在开孔后会出现承载力与开孔率线性递减的关系，这种递减在开孔率增加到一定程度后可能导致承载力完全丧失。相比之下，新型开孔锚固浅基础在低开孔率时承载力基本不会随着开孔率的增加而降低，但当开孔率超过特定限值后，承载力会出现明显的降低。

4、因此，现有技术未能提供一种适用于新型开孔锚固浅基础的有效的抗滑承载力评估方法，特别是在计算最优开孔率方面存在显著的不足。针对这一技术挑战，本发明提出了一种新型开孔锚固浅基础的承载力和最优开孔率计算方法，旨在填补现有技术的空白，并提供一种更加精确、可靠的设计手段。

技术实现思路

1、针对现有技术的不足，本发明提供了一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，使用极限分析上限解思路，构建不同开孔率条件下的破坏机构，可以准确评估不同开孔率条件下新型开孔锚固浅基础承载能力，并有效计算新型开孔锚固浅基础的最优开孔率。

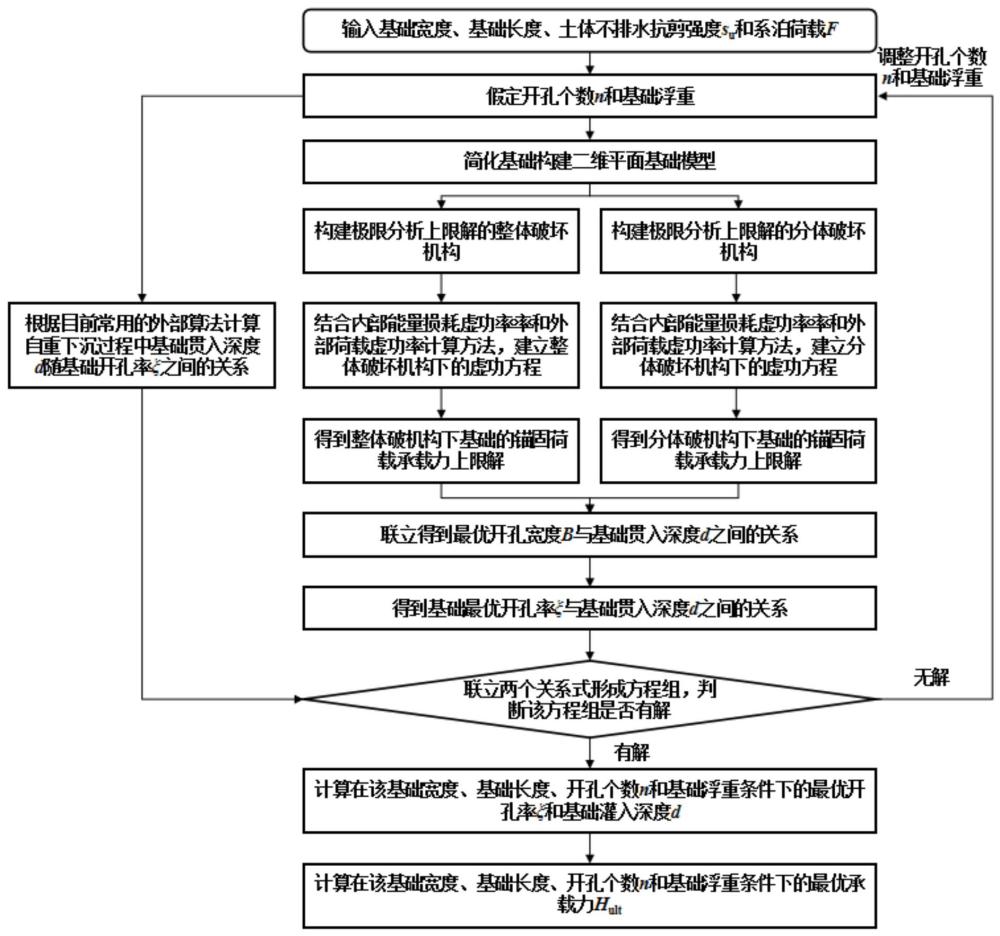
2、为实现以上目的，本发明通过以下技术方案予以实现一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，包括以下步骤：

3、根据基础埋深、基础宽度、基础长度以及开孔个数，简化开孔锚固浅基础为二维平面基础模型；

4、分别构建整体承载模式下和分体承载模式下的破坏机构；

5、根据所述二维平面基础模型，建立整体破坏机构和分体破坏机构的抗滑承载力极限分析上限解虚功率方程；

6、通过虚功率方程，对整体破坏模式和分体破坏模式的承载力进行分析，分别求解得到整体破坏模式和分体破坏模式下的水平向极限锚固承载力；

7、联立分体破坏机构和整体破坏机构下的水平向极限锚固承载力的计算结果，确定最优开孔宽度和开孔率。

8、优选的，所述虚功率方程利用开孔锚固浅基础的开孔部分与相邻的地基土体接触区域形成的内部夹角，来确定水平向极限承载力。

9、优选的，所述整体破坏机构下的承载力采用的虚功率方程公式为：

10、

11、其中，为整体破坏机构条件下的水平向极限锚固承载力；为基础埋深，表示从地面到基础底部的垂直距离；为开孔锚固浅基础的开孔部分与相邻的地基土体接触区域形成的内部夹角，为弧度制；为栅栏板宽度，表示开孔锚固浅基础中非开孔部分的水平宽度；为开孔宽度，表示开孔锚固浅基础中开孔部分的水平宽度；表示开孔个数；为原状土体的不排水抗剪强度；为荷载作用速率，用于计算整体破坏机构条件下的虚功率。

12、优选的，进一步包括根据极限分析上限解原理，求解满足所述整体破坏机构下的承载力采用的虚功率方程等式条件下的最小值，得到整体破坏机构条件下的水平向极限锚固承载力，公式为：

13、。

14、优选的，计算所述分体破坏机构下的极限抗滑承载力采用的虚功率方程公式为：

15、

16、其中，为分体破坏机构条件下的水平向极限锚固承载力。

17、优选的，进一步包括根据极限分析上限解原理，求解满足所述分体破坏机构下的承载力采用的虚功率方程等式条件下的最小值，得到分体破坏机构条件下的水平向极限锚固承载力，公式为：

18、。

19、优选的，所述确定最优开孔宽度和开孔率是通过使用计算整体破坏模式和分体破坏模式下的水平向极限锚固承载力等式条件下提取的参数计算得到

20、其中，开孔宽度公式为：；

21、其中，开孔率公式为：。

22、优选的，所述方法还包括：将得到的最优开孔宽度和最优开孔率带入所述承载力的计算，求解在该基础尺寸和埋深条件下最优设计锚固基础所能提供的极限承载力。

23、本发明还提供一种用于计算开孔锚固浅基础的锚固承载力和最优开孔率的装置，包括：

24、输入模块，用于接收关于开孔锚固浅基础的参数输入，包括基础埋深、基础宽度、基础长度及开孔个数；

25、处理模块，包括一个或多个处理器，配置为：

26、根据接收到的参数简化开孔锚固浅基础为二维平面基础模型；

27、分别构建整体承载模式下和分体承载模式下的破坏机构；

28、计算整体破坏机构和分体破坏机构的水平向极限锚固承载力；

29、计算模块，与处理模块相连，并配置为根据处理模块构建的破坏机构计算水平向极限锚固承载力，确定最优开孔宽度和开孔率，并求解在该基础尺寸和埋深条件下最优设计锚固基础所能提供的极限承载力；

30、输出模块，用于展示计算结果，包括极限抗滑承载力、最优开孔宽度及开孔率。

31、本发明还提供一种计算机设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述计算机程序时，实现如上述的方法。

32、本发明还提供一种存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现如上述的方法。

33、本发明提供了一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法。具备以下有益效果：

34、1、本发明充分考虑了新型开孔锚固基础在入泥之后，结构与土体之间形成的良好接触条件，考虑了结构和土体作为整体的受力模式，使计算结果更为可靠、合理。

35、2、本发明可以快速计算新型开孔锚固基础的开孔宽度及最优开孔率，方便新型开孔锚固基础的设计和使用。

技术特征：

1.一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，其特征在于，包括以下步骤：

2.根据权利要求1所述的一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，其特征在于，所述虚功率方程利用开孔锚固浅基础的开孔部分与相邻的地基土体接触区域形成的内部夹角，来确定水平向极限承载力。

3.根据权利要求2所述的一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，其特征在于，所述整体破坏机构下的承载力采用的虚功率方程公式为：

4.根据权利要求3所述的一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，其特征在于，进一步包括根据极限分析上限解原理，求解满足所述整体破坏机构下的承载力采用的虚功率方程等式条件下的最小值，得到整体破坏机构条件下的水平向极限锚固承载力，公式为：

5.根据权利要求3所述的一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，其特征在于，计算所述分体破坏机构下的极限抗滑承载力采用的虚功率方程公式为：

6.根据权利要求5所述的一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，其特征在于，进一步包括根据极限分析上限解原理，求解满足所述分体破坏机构下的承载力采用的虚功率方程等式条件下的最小值，得到分体破坏机构条件下的水平向极限锚固承载力，公式为：

7.根据权利要求1所述的一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，其特征在于，所述确定最优开孔宽度和开孔率是通过使用计算整体破坏模式和分体破坏模式下的水平向极限锚固承载力等式条件下提取的参数计算得到；

8.根据权利要求1所述的一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，其特征在于，所述方法还包括：将得到的最优开孔宽度和最优开孔率带入所述承载力的计算，求解在该基础尺寸和埋深条件下最优设计锚固基础所能提供的极限承载力。

9.一种用于计算开孔锚固浅基础的锚固承载力和最优开孔率的装置，实施如权利要求1-8任一项所述的方法，其特征在于，包括：

10.一种存储介质，其上存储有计算机程序，其特征在于，该计算机程序被处理器执行时实现如权利要求1-8任一项所述的方法。

技术总结本申请涉及建筑工程和土木工程领域，公开了一种开孔锚固浅基础的锚固承载力和最优开孔率计算方法，包括：S1、根据基础埋深、宽度、长度及开孔个数，将开孔锚固浅基础简化为二维模型；S2、构建整体和分体承载模式下的破坏机构；S3、建立整体和分体破坏机构的抗滑承载力极限分析上限解虚功率方程；S4、求解整体和分体破坏模式下的水平向极限锚固承载力；S5、联立分体和整体破坏机构下的计算结果，确定最优开孔宽度和开孔率；S6、将最优开孔宽度和开孔率带入抗滑极限承载力计算公式，求得最优设计锚固基础的抗滑极限承载力。本发明考虑了开孔锚固基础与土体形成的良好接触，考虑了结构和土体作为整体的受力模式，计算结果更为可靠合理。技术研发人员：汪嘉钰,刘润,陈炳桦,练继建,林大明受保护的技术使用者：天津理工大学技术研发日：技术公布日：2024/7/29