一种基于稳定节点光滑有限元法的磁滞问题求解方法与流程

本申请涉及磁滞问题求解，特别是涉及一种基于稳定节点光滑有限元法的磁滞问题求解方法。

背景技术：

1、计算铁磁材料的磁滞问题是计算电磁学中的重大挑战。目前，大多技术直接忽略铁磁材料的磁滞，直接采用b-h曲线对铁磁材料进行非线性计算，从而导致计算问题的精度下降。

2、jiles-atherton（j-a）磁滞模型，该模型由于构造效率较高且很容易和有限元数值算法进行耦合，因此j-a模型在有限元电磁算法上得到快速发展且具有广泛的应用，目前已经应用于二维和三维的矢量计算、各向异性计算和逆运算。然而，j-a模型也存在两大挑战，第一个挑战为该模型和线性非结构网格耦合处理复杂的电子设备的磁滞问题时，其计算精度和可靠性无法得到保证；第二个挑战是j-a模型具有很强的非线性且其非线性和历史相关，因此收敛性较难。

技术实现思路

1、基于此，有必要提供一种基于稳定节点光滑有限元法的磁滞问题求解方法，该方法包括：

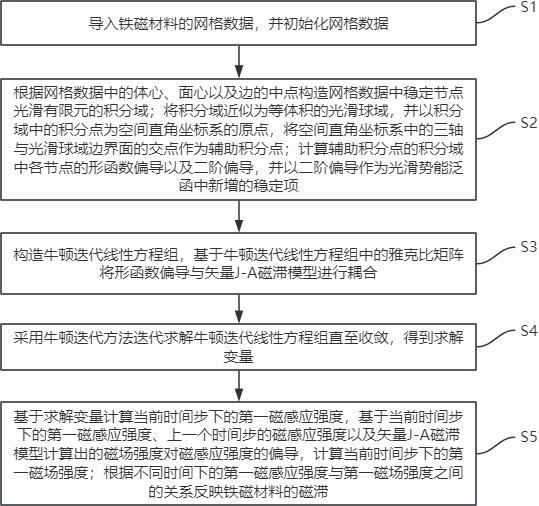
2、s1：导入铁磁材料的网格数据，并初始化所述网格数据；

3、s2：根据所述网格数据中的体心、面心以及边的中点构造网格数据中稳定节点光滑有限元的积分域；将所述积分域近似为等体积的光滑球域，并以积分域中的积分点为空间直角坐标系的原点，将空间直角坐标系中的三轴与光滑球域边界面的交点作为辅助积分点；计算辅助积分点的积分域中各节点的形函数偏导以及二阶偏导，并以所述二阶偏导作为光滑势能泛函中新增的稳定项；

4、s3：构造牛顿迭代线性方程组，基于所述牛顿迭代线性方程组中的雅克比矩阵将所述形函数偏导与矢量j-a磁滞模型进行耦合；

5、s4：采用牛顿迭代方法迭代求解所述牛顿迭代线性方程组直至收敛，得到求解变量；

6、s5：基于所述求解变量计算当前时间步下的第一磁感应强度，基于所述当前时间步下的第一磁感应强度、上一个时间步的磁感应强度以及所述矢量j-a磁滞模型计算出的磁场强度对磁感应强度的偏导，计算当前时间步下的第一磁场强度；根据不同时间下的第一磁感应强度与第一磁场强度之间的关系反映铁磁材料的磁滞。

7、有益效果：该方法提高了求解磁滞问题的计算精度和收敛稳定性，实现了复杂工程电磁场铁磁材料中高计算精度和可靠性需求；另外，实现了矢量j-a磁滞模型在磁记录、变压器、电机等复杂工程电磁场中的广泛应用。

技术特征：

1.一种基于稳定节点光滑有限元法的磁滞问题求解方法，其特征在于，包括：

2.根据权利要求1所述的基于稳定节点光滑有限元法的磁滞问题求解方法，其特征在于，s2中，所述辅助积分点包括六个，六个所述辅助积分点下在节点i处的形函数偏导分别为：

3.根据权利要求2所述的基于稳定节点光滑有限元法的磁滞问题求解方法，其特征在于，二阶偏导的计算公式为：

4.根据权利要求3所述的基于稳定节点光滑有限元法的磁滞问题求解方法，其特征在于，s2还包括在所述积分域中计算六个辅助积分点下的形函数偏导之间的相互点乘；计算公式为：

5.根据权利要求4所述的基于稳定节点光滑有限元法的磁滞问题求解方法，其特征在于，s3中，所述牛顿迭代线性方程组的表达式为：

6.根据权利要求5所述的基于稳定节点光滑有限元法的磁滞问题求解方法，其特征在于，基于雅克比矩阵将光滑稳定节点有限元中的所述形函数偏导与矢量j-a磁滞模型进行耦合包括：

7.根据权利要求5所述的基于稳定节点光滑有限元法的磁滞问题求解方法，其特征在于，s4中，牛顿迭代方法迭代求解过程包括：

8.根据权利要求1所述的基于稳定节点光滑有限元法的磁滞问题求解方法，其特征在于，基于所述求解变量计算当前时间步下的第一磁感应强度，计算公式为：

9.根据权利要求8所述的基于稳定节点光滑有限元法的磁滞问题求解方法，其特征在于，计算当前时间步下的第一磁场强度的计算公式为：

技术总结本申请涉及一种基于稳定节点光滑有限元法的磁滞问题求解方法，包括：根据网格数据中的体心、面心以及边的中点构造网格数据中稳定节点光滑有限元的积分域；将空间直角坐标系中的三轴与光滑球域边界面的交点作为辅助积分点；计算辅助积分点下的形函数偏导；基于牛顿迭代线性方程组中的雅克比矩阵将形函数偏导与矢量J‑A磁滞模型进行耦合；采用牛顿迭代方法迭代求解牛顿迭代线性方程组直至收敛，得到求解变量；基于求解变量计算第一磁感应强度，基于第一磁感应强度和磁场强度对磁感应强度的偏导计算第一磁场强度；根据第一磁感应强度与第一磁场强度之间的关系反映铁磁材料的磁滞。该方法提高了求解磁滞问题的计算精度和收敛稳定性。技术研发人员：郑景宇受保护的技术使用者：湖南迈曦软件有限责任公司技术研发日：技术公布日：2024/7/29