一种基于磷虾群算法改进BP神经网络模型的非饱和土壤水力参数预测方法

本发明属于地下水污染与修复领域，具体涉及一种基于磷虾群算法(krill herdalgorithm，kha)改进bp神经网络模型的非饱和土壤水力参数的预测方法，可应用于地下水补给、污染物运移等数值模拟过程。

背景技术：

1、地下水污染修复在实际工作中，场地的复杂条件和工程实施可能会给地下水污染修复带来诸多问题。例如，过高、过低的渗透性，地球化学、微生物条件制约，持续的污染释放，复杂混合污染物以及工程实施对地下水流场形成剧烈扰动等，导致地下水污染修复过程难以精准控制。

2、地下水数值模拟能可视化分析研究地下水流和溶质运移问题，具有直观性、有效性和灵活性的特点。构建地下水污染概念模型，需要对研究区域的包气带进行概化，以获得污染物在包气带中的迁移时间和通量，准确估算地下水系统的污染源强。构建包气带溶质运移模型，需确定模型的关键参数，包括土壤水分特征曲线van genuchten模型参数、土壤导水率等土壤水力参数，土壤孔隙度、土壤容重、粒径分布等土壤理化参数，以及土壤污染物吸附参数。土壤水力参数是水分运动方程的重要参数，包括土壤水分特征曲线(the soilwater characteristic curve，swcc)、土壤导水率、水分扩散率和弥散度等，其中土壤水分特征曲线和土壤导水率是反映土壤水动力的最重要物理参数，也是目前研究最关注的参数。土壤水分特征曲线是描述土壤体积含水率与基质势关系的函数曲线。土壤导水率是土壤压力水头的函数，其随着压力水头的降低而降低。土壤水力参数的可靠性在很大程度上影响着水分运动模拟的灵敏性，对水分运动模拟预测结果有直接影响。

3、在场地地下水污染修复工作中，土壤自身的高度异质性导致了土壤水力参数的批量获取存在着技术难题。土壤水力参数受到土壤容重、土壤颗粒组成、土壤孔隙度以及有机质含量等土壤理化性质和大气降水等众多因素影响，但上述影响因素对土壤水力参数的综合影响机制目前尚未研究清楚。同时土壤结构本身具有易破碎性，直接测定必然涉及到大量取样测试的问题，破坏土壤的天然结构，当采样条件有限或研究大尺度条件下水力参数时，工作量大，难以保证数据的完整，导致土壤水里参数的测试数据存在偏差。因此，土壤水力参数具有复杂性、随机性和区域变异性特征，致使了现有的土壤水分特征曲线、土壤导水率等土壤水力参数测定技术都存在不同的局限性。

4、目前获取土壤水分特征曲线的主要方法可以分为两类，直接测定法和间接测试法。直接测定法包括张力计法、压力膜法、离心机法、砂芯漏斗法、平衡水汽压法等测定方法，通过采集原状土，影响扰动土和原状土的脱水、吸水过程，测定多个土壤吸力下土壤水分，根据土壤水吸力与土壤含水率的关系，从而绘制出土壤水分特征曲线。其中，前3种直接测定土壤水分特征曲线的方法最为普遍应用，张力计法可测定0～0.08mpa的吸力范围(土壤有效水的50％～70％)，是监测田间土壤水分动态的唯一手段，但表头张力计存在准确度较差，有可能改变特征曲线的形状及测定范围有限的缺陷。压力膜法测定特征曲线的形状与土壤固有的特征曲线相符，适用于土壤水分动态模拟。但它测定周期长，步骤烦琐，存在土壤体积变化问题。离心机法比其他方法操作简单、省时，可测定较宽的吸力范围，但离心机法在测定过程中土壤体积质量随转速会发生明显的变化，特别是黏粒量高的土壤。同时，该方法在不同温度条件的测试结果下有明显异。

5、土壤水分特征曲线间接测试法包括经验公式法、分形几何法、土壤形态学方法、土壤转换函数方法等，利用易获取的土壤颗粒大小分布、土壤容重等基本性质预测土壤水力特性参数。文献(辛琳，等.“土壤水分特征曲线的4种经验公式拟合研究.”山西农业科学，02(2018)：256-259.)报道了土壤水力参数测试的经验公式法，该方法选取gardner、van-genuchten、mckee-bumb和frdlund-xing模型拟合swcc曲线，结果发现除van genuchten模型拟合精度较高(r2＝0.994)，其他模型效果较差(r2＝0.937-0.993)。并且，还需要大量实测数据，且不同经验模型适用范围不同，结果存在一定的不确定性。文献(郑子成，等.“基于分形理论的设施土壤水分特征曲线研究.”农业机械学报，43(2012)：49-54.)报道了土壤水力参数测试的分形几何法，该方法利用土壤粒径分布的分形维数结合brooks-corey经验模型，对设施土壤的水分特性曲线进行预测，预测精度较高(r2＝0.986-0.992)。但是，大部分的分形模型忽略了土壤颗粒表面化学性质、矿物学特性、流体性质等因素对土壤水力参数的影响，不能完整刻画水分持留过程，存在一定的局限性。文献(刘建立，等.“预测土壤水力性质的形态学网络模型应用研究.”土壤学报，02(2004)；218-224)报道了基于ct测试和网络模型相结合的土壤形态学方法，预测土壤的水力性质，预测结果与土壤水分特征曲线实测值相比存在较大的误差。同时，这种形态学方法的实验精度要求在微米级别，其仪器和分析过程十分昂贵，超过了直接实验测定水力性质的成本。文献(李爽，等.“基于土壤理化性质估计土壤水分特征曲线van genuchten模型参数.”地理科学,38(2018)：1189-1197)报道，通过测定东北黑土区土壤水分、机械组成、有机质和容重等指标，利用土壤转换函数rosetta模型估计了van genuchten模型的参数。该模型对砂粒含量较高的重度侵蚀黑土拟合较差(r2＝0.48)。同时，该模型仅适用于黑龙江省西北部土壤，没有考虑到土壤水力参数的研究区域变异性问题。

6、目前获取土壤导水率主要方法大致可以分为两类：直接测定法和间接推求法。直接测定法可分为稳态和瞬态两类，稳态法有水头控制法、长柱入渗法、基质通量势法和分离土柱法等。瞬态法有瞬时剖面法、压力板出流法和玻尔兹曼变换法等。但上述测定方法耗时、昂贵、烦琐，测定范围较窄，可获得的试验数据不能代表土壤水力特征完整关系，而且逆问题求解法也存在同样的限制以及参数的非唯一性。

7、土壤导水率的间接推求法是以统计孔隙大小分布burdine、mualem模型为基础，结合土壤水分持水特征模型拟合实测的数据获得土壤导水率。文献(shao m-a，et al.“determining the hydraulic conductivi2 ty and water diffusivity ofunsaturated soils from soil water redistri2 bution.”memoir of niswc,academiasinica and ministry of water conservancy,2(1985):47-53)报道了土壤水力参数测试的间接推求法，该方法是以土壤水分再分布过程的水分运动基本方程以及湿润锋湿度与土壤剖面平均湿度的一定函数关系(幂函数)为理论基础,结合土壤水分特征曲线推求出土壤的导水率。它具有理论基础坚实，测定准确度高，测定范围广(中湿与低湿情况)和设备简单等特点。但是，该方法也存在湿润锋湿度测定不标准和假定函数关系应用范围限制的缺陷。

8、在实际污染场地中，不同区域土壤理化性质通常差异较大，致使土壤水力参数在同一土壤的不同空间位置的测定值有较大差别。当溶质在包气带和含水层的迁移过程中，土壤水力参数随着空间地理位置的变化不断发生改变，使得实际包气带-含水层地下水溶质迁移体系复杂程度远大于实验室模拟尺度，不能反映实际污染场地的土壤水力参数的变化情况。目前，没有综合考虑土壤样点时空代表性和差异性的非饱和土壤水力参数预测模型，尤其关注土壤理化性质(土壤容重、粘粒含量、粉粒含量、砂粒含量、有机质含量、土壤孔隙度等)和区域气候条件影响的非饱和土壤水力参数预测模型。

9、因此，本发明围绕修复场地土壤水力参数因空间变异性强、批量获取难等技术难题，建立了一种基于磷虾群算法改进bp神经网络模型的土壤水力参数预测方法。首先，汇总与统计了面向陆面模拟的中国土壤数据集、面向陆面过程模型的中国土壤水文数据集和场地案例数据，构建了涵盖土粒密度、土壤容重、土壤质地、土壤颗粒组成以及有机质含量等参数的土壤属性数据集。筛选与识别出与土壤水力参数有较大关联度的土壤理化参数及气候条件参数，构建了一种基于磷虾群算法改进bp神经网络模型的土壤水力参数预测方法，为预测场地土壤水力参数提供理论支撑与模型参考。

技术实现思路

1、本发明的目的在于克服空间变异性强、批量获取难等技术难题，提供一种基于国内各省份土壤理化性质和气候条件数据，使用kha-bp神经网络模型对不同空间区域的土壤水力参数进行预测的方法。

2、本发明的技术方案：

3、一种基于磷虾群算法改进bp神经网络模型的非饱和土壤水力参数预测方法，包括以下步骤：

4、步骤s1：获取土壤理化性质和年均降雨量数据，对数据进行预处理，包括归一化处理、相关性分析；

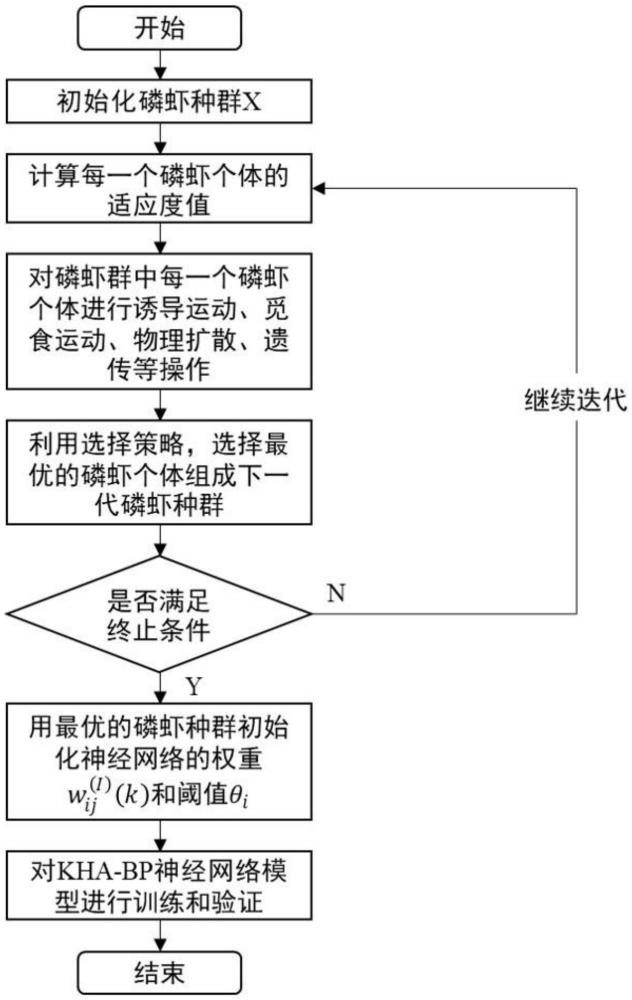
5、步骤s2：利用磷虾群算法的寻优机理对bp神经网络模型的网络权重和阈值进行优化，构建kha-bp神经网络模型；

6、步骤s2.1，采用磷虾群优化算法寻找最优的迭代权重和阈值参数，根据迭代权重和阈值参数的范围初始化种群x＝{x1，x2，x3…xn}，计算均方误差作为每个种群的适应度k＝{k1，k2，k3…kn}；种群速度的更新公式为：

7、

8、式中，ni为邻居磷虾的诱导运动，fi为磷虾群体的觅食运动，di为磷虾群体的物理扩散(扰动)；磷虾种群个体会根据种群的速度移动到下一个位置，完成一次位置更新；

9、诱导运动是邻居种群对于该种群的影响，其表达式为：

10、

11、式中，αi为诱导方向，由邻居位置和最优适应度个体位置决定；wn为惯性权重在[0,1]范围之内；为先前诱导运动；nmax为最大的诱导速度；

12、觅食运动是寻找食物的中心位置，即最佳权重和阈值参数的位置对于种群的吸引，其表达式为：

13、

14、式中，vf为觅食速度；bi为觅食方向，由食物和最优适应度个体位置决定；为先前觅食运动；wf为惯性权重在[0,1]范围之内；

15、物理扩散(扰动)为种群随机行为，随迭代次数的增加而减少。

16、

17、式中，i为迭代次数；δ为随机方向矢量，在[-1,1]之间；dmax为最大扰动速度；imax为迭代总数；

18、完成位置更新之后，采用基因繁殖机制，使用交叉操作对种族进行更新，然后继续下一次迭代。迭代完成后，获得最优适应度的种群位置，即为最优磷虾种群。

19、步骤s2.2，优化网络权重和阈值，利用步骤s2.1中得到最优磷虾种群对bp神经网络模型中的权重和阈值进行优化。

20、步骤s3：在步骤s2的kha-bp神经网络模型的基础上，选取输入输出指标，构建基于kha-bp的非饱和土壤水力参数预测模型；

21、步骤s3中构建基于kha-bp的非饱和土壤水力参数预测模型的具体步骤为：

22、步骤s3.1，输入输出指标的选择：选取经步骤s1相关性分析筛选出的与土壤水力参数相关的土壤理化性质和年均降雨量数据作为输入变量，选取土壤水分特征曲线的vangenuchten模型参数(土壤饱和含水率θs、土壤残余含水率θr、尺度参数a和形状参数n)和土壤非饱和导水率k作为输出指标，则基于kha-bp的非饱和土壤水力参数预测模型的输入输出为：

23、输入变量：x1＝粘粒含量，x2＝粉粒含量，x3＝砂粒含量，x4＝土壤容重，x5＝有机质含量，x6＝土壤孔隙度，x7＝ph，x8＝年均降雨量；

24、输出变量：y1＝土壤残余含水率，y2＝土壤饱和含水率、y3＝尺度参数，y4＝形状参数，y5＝土壤非饱和导水率；

25、步骤s3.2，根据步骤s3.1得到的输入输出变量建立模型的样本数据集，并使用mapminmax归一化函数对数据集中的数据进行归一化处理，过程为：

26、

27、式中，xi为样本数据集x的环境数据；ximin和ximax分别为归一化之前的最小值和最大值，完成对样本数据集归一化操作，归一化后数据样本集x′＝{x′1，x′2，x′3，x′4，x′5，x′6，x′7，x′8}，直接用于后续模型建立所需要的输入、输出变量；

28、步骤s3.3，确定网络结构的策略，根据步骤s3.1中选取的输入输出指标，确定网络结构的输入、输出及隐含层的层数，基于kha-bp的非饱和土壤水力参数预测模型的输入层的节点数m＝8，输出层节点数n＝5，其中隐层神经元的个数通过下式确定

29、

30、式中，s为隐含层节点数目，m为输入层节点数目，n为输出层节点数目，a为1～10之间的调节常数；

31、步骤s3.4，激活函数的选取，输入层采用tansig激活函数，输出层采用purelin激活函数，选取trainlm函数作为非饱和土壤水力参数预测模型的训练函数；

32、步骤s3.5，采用rsme和数据统计指标决定系数r2来对非饱和土壤水力参数预测模型的预测结果进行评估；决定系数r2的数学形式如下：

33、

34、式中，yi是实际值，fi是预测值，是实际值的平均值，i为样本数据集中数据序号；

35、当预测值越接近于实际值，即拟合程度越高，两者之间的残差就会越小，残差平方和∑i(yi-fi)2就会相应减少；这一点体现在r2上就会使r2的数值增大，因此，r2可以有效地反映预测值和实际值之间的拟合程度，评估模型预测结果的优劣。

36、均方根误差(rmse)的计算方式如下所示：

37、

38、式中，t为数据集中数据个数；

39、rmse是均方误差(mse)的平方根，而均方误差是预测值与真实值偏差的平方与观测次数的比值，可以有效衡量观测值同真值之间的偏差。rmse越大，说明偏差越大，模型拟合程度越低。

40、步骤s4：利用经过归一化处理的数据集对步骤s3中建立的基于kha-bp的非饱和土壤水力参数预测模型进行学习和训练，最终完成对土壤水力参数的预测；

41、步骤s4中利用经过归一化处理的数据集对步骤s3中建立的基于kha-bp的非饱和土壤水力参数预测模型进行学习和预测的具体步骤为：

42、步骤s4.1，训练数据集的选择策略，利用步骤s3.2中经过归一化处理的数据集，从中选择70％的数据集作为训练数据集，剩余30％的数据集作为测试数据集；

43、步骤s4.2，磷虾群算法中关键参数的设置，磷虾的种群数量popsize＝30，磷虾群的决策变量上界值为ub＝3，磷虾群的决策变量下界值lb＝-3，最大迭代次数maxgen＝50，其中变量的维数d＝89，具体是在步骤s3.3的基础之上通过如下公式计算

44、d＝m×s+s+s×n+n (9)

45、式中，m，n，s分别为网络的输入层神经元、输出层神经元以及隐藏层神经元的个数；

46、步骤s4.3，在步骤s4.2中磷虾群算法参数设置的基础上，使用步骤s4.1中选择的训练数据集对基于kha-bp的非饱和土壤水力参数预测模型进行训练，在网络训练过程中相关的参数设置：学习速率为0.01，训练次数为1000，最小训练误差为0.00001；

47、步骤s4.4，通过步骤s4.1～s4.3训练得到了基于kha-bp的非饱和土壤水力参数预测模型，使用步骤s4.1中选择的测试数据集，对模型的预测效果进行测试统计分析和实验仿真。

48、本发明的有益效果：本发明基于国内各省份的土壤理化性质和气候条件数据，改善了土壤水力参数存在空间变异性这个问题，同时提高了土壤水力参数的预测精度，降低了网络了迭代次数。本发明主要将磷虾群算法引入到bp神经网络模型中，利用磷虾群在觅食过程中，种群聚集、寻找食物和搜索生存空间三种运动同时运行的机制，对神经网络模型的权重和阈值参数进行优化，从而可以减少预测模型的迭代次数，提高模型预测的准确率。