基于径向基神经网络的无人直升机自抗扰容错控制方法

本发明属于无人直升机容错控制，具体涉及基于径向基神经网络的无人直升机自抗扰容错控制方法。

背景技术：

1、无人直升机由旋翼提供升力及操纵力矩，具备悬停、任意方向飞行以及小区域起降等优良的飞行特性，因此被广泛应用于军事及民用领域。随着无人直升机性能的日益提升，其飞行控制系统对传感器的要求也越来越高。此外，无人直升机面临的恶劣工作环境容易造成机载传感器发生故障，如果故障传感器信号反馈给控制系统，势必导致错误控制，严重者将发生坠机，此时有效的传感器容错控制是实现安全飞行的关键和前提。

2、近年来，针对飞行器传感器故障的容错控制研究受到关注。wang等提出了一种基于自适应滑模控制和自适应边界层的四旋翼飞行器双自适应容错控制策略，该方法能够在模型及故障信息不确定的情况下进行补偿，并采用最小间断控制增益，显著降低了控制抖振效果，但不同类型的外部扰动问题尚未得到研究，现有技术中提出了一种利用离线训练的深度神经网络对故障进行估计，并与非线性动态反演相结合，能够在不同故障类型和严重的风扰动条件下着陆飞机，但该方法不能做到实时估计故障信息，离工程实践还有一段距离。

3、自抗扰控制(active disturbance rejection control，adrc)将系统内部及外部扰动视为总扰动，通过状态扩张的办法建立扩张状态观测器，将总扰动用扩张状态进行估计，用于系统控制实时补偿。adrc不依赖于精确数学模型，克服了不确定性内外扰动的干扰，使控制系统具有较强的鲁棒性，已在工程实践和理论分析角度得到了有力的验证。由于非线性自抗扰控制技术的调节参数过多,限制了自抗扰的实际应用。现有技术中还公开了线性自抗扰控制(linear active disturbance rejection control,ladrc)技术,使得调节工作量大大降低，极大地促进了自抗扰控制技术的研究与应用。同时，径向基神经网络(radial basis function neural network，rbfnn)自适应能力强，且能够逼近任意连续函数，因此本发明公开了一种基于径向基神经网络的无人直升机自抗扰容错控制方法，引入状态输出信号积分变量对原系统进行增广，在此基础上，用rbfnn估计未知传感器故障，用ladrc技术获取无人直升机状态量及内外总扰动估计值，并将无人直升机系统转换为不包含扰动的标准积分串联型结构。该方法结构简单，自适应能力强，能够解决各种类型的传感器故障问题，具有较高的工程应用价值。

技术实现思路

1、本发明所要解决的技术问题是提供基于径向基神经网络的无人直升机自抗扰容错控制方法，解决含有传感器故障的无人直升机容错飞行控制问题。

2、本发明为了解决上述技术问题采用以下技术方案：本发明设计了基于径向基神经网络的无人直升机自抗扰容错控制方法，基于实时目标指令，实时执行如下步骤a至步骤c，实现对无人直升机的实时容错控制；

3、步骤a、根据无人直升机的6自由度运动特征，构建无人直升机所对应的姿态模型，在此基础上引入传感器故障模型，建立包含传感器故障的无人直升机姿态模型，然后进入步骤b；

4、步骤b、基于无人直升机所对应的姿态模型，根据实时目标指令，构建无人直升机姿态容错控制回路，获得无人直升机的姿态控制矢量；然后进入步骤c；

5、步骤c、根据无人直升机的姿态控制律输出量，针对无人直升机进行容错控制。

6、作为本发明的一种优选技术方案：所述步骤a中，根据无人直升机的6自由度运动特征，构建无人直升机所对应的运动学模型如下：

7、

8、

9、

10、

11、其中，v＝[u v w]t为无人直升机的前飞速度、横向速度、垂向速度；s＝[p q r]t为无人直升机的滚转角速度、俯仰角速度、偏航角速度；α＝[φ θ ψ]t为无人直升机的滚转欧拉角、俯仰欧拉角、偏航欧拉角；p＝[x y z]t为无人直升机地面坐标；m为无人直升机的全机质量；f、m分别为无人直升机全机各部件的合外力、以及合外力矩；i为无人直升机惯性矩矩阵，ω为无人直升机三轴角速率反对称矩阵，reb为机体坐标系到地面坐标系的转换矩阵，e为无人直升机机体角速度到欧拉角速度的转换矩阵。

12、以姿态模型为例，式(1-2)和式(1-3)可表示为

13、

14、

15、式中，w为外部扰动，uc＝[δlon δlat δtr]为纵向变距、横向变距和尾桨变距操纵量构成的控制矢量。联立式(1-5)与(1-6)可得二阶姿态模型

16、

17、其中，f3＝df1/dt,f1，f2，b为相应缩写。将α之外的内部动态特性、各通道之间的操纵耦合以及外扰视为总扰动，记为则式(1-7)变为

18、

19、式中，b0α为姿态控制增益矩阵，俯仰、滚转、偏航通道控制量uci与输出量yαi＝αi构成单输入-单输出关系。

20、式(1-8)以状态空间形式可表示为

21、

22、式中，x1＝[φ θ ψ]t，y表示系统输出。

23、一般的，传感器故障分为恒偏差故障、漂移故障与恒增益故障。基于此，传感器故障模型表示如下

24、y＝msx1+yt       (1-10)

25、式中，y为系统传感器输出的实际测量值，ms＝[ml ma mc]为传感器增益系数矩阵，yt＝[yl ya yc]为传感器偏差系数矩阵且ytmin<yt<ytmax，存在上下边界。

26、联立式(1-9)与(1-10)，可得包含传感器故障的无人直升机姿态模型为

27、

28、式中，fg(x1)＝(ms-i)x1+yt。

29、作为本发明的一种优选技术方案：所述步骤b中，基于无人直升机所对应的姿态模型，根据实时目标指令，按如下构建无人直升机姿态容错控制回路，获得无人直升机的姿态控制矢量；

30、由于姿态角传感器存在未知故障，系统输出测量值不能直接应用于ladrc的扩张状态观测器，因此采用状态増广的方法改造扩张状态观测器，采用rbfnn对传感器未知故障进行估计，解决传感器故障对系统状态真实值估计的影响。

31、定义系统输出信号的积分信号为

32、

33、综合式(1-11)与(1-12)，得

34、

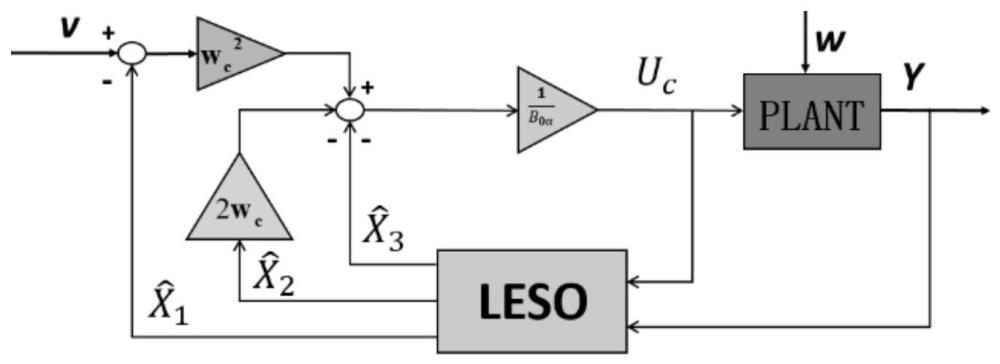
35、对増广系统(1-13)设计如下基于rbfnn的的线性扩张状态观测器(leso)

36、

37、式中，分别为x0,x1,x2的估计值；为扩张状态，表示对系统总扰动的估计值；表示采用rbfnn对姿态角传感器未知故障的估计，是权重系数的估计权值，其中：

38、

39、cj＝[c1j c2j … cnj]t      (1-16)

40、式中，cj为隐含层第j节点神经元高斯基函数中心点的坐标向量；bj为其高斯基函数的宽度，n表示输入变量数量。

41、ladrc控制律输出uc为：

42、

43、

44、式中，wc表示为控制器带宽，当系统输入v为常值时，v2＝0,v3＝0.

45、姿态模型(1-11)的经过控制律(1-17)的变换，转变为

46、

47、在扩张状态估计值补偿下系统成为积分串联型线性被控对象，即

48、

49、系统(1-13)中异于标准积分串联型部分视为总扰动(包括内扰和外扰)经leso估计，作为控制律的补偿，将带扰动的非线性系统处理成式(1-20)形式的标准积分串联型系统，实现了非线性被控对象的动态补偿线性化处理。通过rbfnn估计传感器故障fg(x1)，使系统输出信息传递到leso的串联型结构中不包含传感器的故障信息，保证为实际x1的估计值。

50、本发明所述基于径向基神经网络的无人直升机自抗扰容错控制方法，采用以上技术方案与现有技术相比，具有以下技术效果：

51、本发明所设计基于径向基神经网络的无人直升机自抗扰容错控制方法，建立无人直升机的姿态模型，并设计基于rbfnn的线性扩张状态观测器估计传感器故障与内外总扰动，据此构建无人直升机容错控制方法，能有效避免无人直升机姿态控制系统受传感器故障影响而不能稳定控制飞行姿态，本专利提出的基于径向基神经网络的无人直升机自抗扰容错控制方法能够有效克服传感器故障影响，并且抗干扰能力强，鲁棒性好。