基于改进稀疏贝叶斯算法的级联信道估计方法和介质

本发明属于无线通信，尤其是涉及一种基于改进稀疏贝叶斯算法的级联信道估计方法和介质。

背景技术：

1、信道估计技术借助于参考信号或发送数据的统计特性，估计衰落信道中各多径分量的衰落系数，能够提高信号传输的可靠性、增强通信系统的容量、降低传输功耗并支持高速数据传输，在无线通信系统中具有至关重要的作用。随着移动无线通信技术飞速发展，可重构智能表面(ris)作为第5代(5g)甚至第6代(6g)无线通信的候选技术，受到了越来越多的关注。ris是一种由大量无源反射元件组成的数字控制元表面，可以控制电磁波在通信信道中的传播以实现各种功能，如覆盖扩展、信道功率和信道秩的提高以及干扰抑制等。研究表明，ris可以用于增强许多现有技术，例如，添加ris可以增加通信距离，并提高毫米波(mmwave)和太赫兹(thz)频带的最佳接收功率，ris也可被用于增强期望的信号功率或抑制干扰，同时提高安全性。因此，可以考虑利用ris的潜在性能增益，通过ris辅助网络获得准确的信道状态信息(csi)。

2、ris辅助的无线通信系统与中继网络类似，包含单独信道和级联信道两种链路信息，前者描述了两个终端之间的散射特性，后者对应从基站到ris再到终端的路径。但不同于反向散射或中继网络，ris没有射频链，只能以可重新配置的方式将入射信号反射到期望的方向；此外，由于ris缺乏信号处理能力，信道估计的计算任务通常在终端而不是ris节点上实现，因此，单独估计ris到基站的信道和ris到终端的信道是非常困难的，通常需要根据设备发送的导频序列来估计级联的设备ris-bs信道，但具有大量单元的ris反射器会导致多用户系统的导频开销大幅度增高。中国专利申请cn202310382732.0公开了一种基于稀疏贝叶斯学习的信道估计方法，针对ris辅助的毫米波多输入多输出(mimo)通信系统，考虑毫米波信道在角度域的稀疏特点，将信道估计问题转化为结构化的稀疏信号恢复问题，结合稀疏贝叶斯学习框架，设计了一种消息传递迭代估计算法，具有较低的计算复杂度，大大降低了系统的导频开销。但传统稀疏贝叶斯算法中，当观测数据中存在严重的噪声干扰时，固定点更新方程可能无法准确地恢复稀疏信号，从而导致其估计精度在低信噪比情况下较差。因此，需要设计一种级联信道估计方法，进一步提高级联信道估计精度。

技术实现思路

1、本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种基于改进稀疏贝叶斯算法的级联信道估计方法和介质，进一步提高级联信道估计精度。

2、本发明的目的可以通过以下技术方案来实现：

3、本发明提供一种基于改进稀疏贝叶斯算法的级联信道估计方法，包括以下步骤：

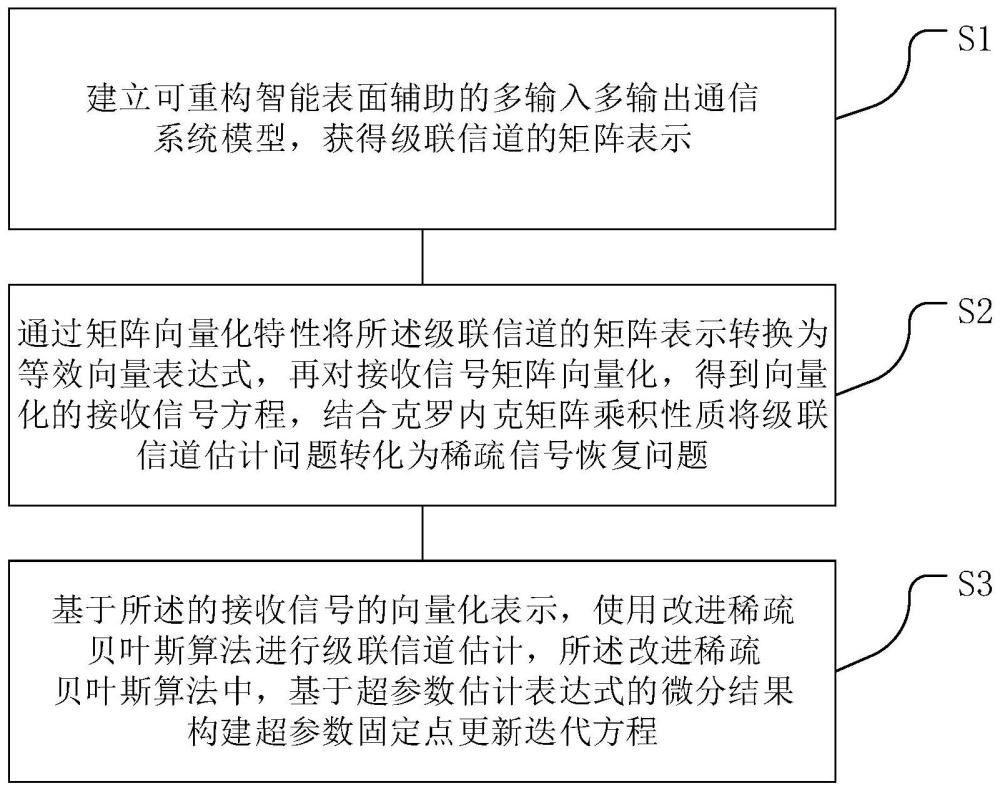
4、s1、建立可重构智能表面辅助的多输入多输出通信系统模型，获得级联信道的矩阵表示；

5、s2、通过矩阵向量化特性通过矩阵向量化特性将所述级联信道的矩阵表示转换为等效向量表达式，再对接收信号矩阵向量化，得到向量化的接收信号方程，结合克罗内克矩阵乘积性质将级联信道估计问题转化为稀疏信号恢复问题；

6、s3、基于所述的接收信号的向量化表示，使用改进稀疏贝叶斯算法进行级联信道估计，所述改进稀疏贝叶斯算法中，基于超参数估计表达式的微分结果构建超参数固定点更新迭代方程；

7、使用改进稀疏贝叶斯算法进行级联信道估计的过程具体如下：

8、s301、根据第一类最大似然估计方法，确定稀疏信号的先验分布；

9、s302、获取接收信号，结合所述稀疏信号的先验分布和第二类最大似然估计方法，获得证据函数；

10、s303、基于所述证据函数取对数的转换结果和第二类最大似然估计方法，获得超参数估计表达式；

11、s304、基于所述超参数估计表达式的微分结果构建超参数固定点更新迭代方程；

12、s305、根据所述超参数固定点更新迭代方程更新超参数，收敛后得到稀疏向量，基于所述接收信号的向量化表示估计级联信道。

13、进一步地，步骤s1中，所述的可重构智能表面辅助的多输入多输出通信系统模型包括基站和用户端，二者之间通过可重构智能表面ris进行信息传输，所述基站和所述可重构智能表面之间、所述可重构智能表面和所述用户端之间的信道为多径信道，所述基站和所述用户端之间级联信道的矩阵表示具体如下：

14、g＝h1θh2＝wraλwbθwuγwrd

15、其中，g为级联信道的矩阵表示，h1∈cr×n为基站-可重构智能表面，h2为可重构智能表面-用户端信道，θ为可重构智能表面中元件的相移，配备r根天线的基站和配备m根天线的用户端采用多输入多输出传输方式，辅助通信的可重构智能表面配备了n个元件，其每个元件具有单独的反射系数和相移，可重构智能表面的每个反射元件通过智能控制器对入射信号重新配置相移和幅度，构成ris的相移幅度矩阵θ，

16、和分别为基站-可重构智能表面信道的到达角aoa和离开角aod所构成的导向矩阵，为基站-可重构智能表面稀疏信道增益矩阵，nb和rb分别为可重构智能表面矩阵和透射角矩阵的网格尺寸，和分别为可重构智能表面-用户端信道中达角aoa和离开角aod所构成的导向矩阵，为可重构智能表面-用户端稀疏信道增益矩阵，nu和mu分别为可重构智能表面矩阵和透射角矩阵的网格尺寸。

17、进一步地，步骤s2中，将级联信道的矩阵表示g三次矩阵向量化转换得到g的等效向量表达式，具体如下：

18、

19、其中，⊙为卡特里-拉奥矩阵乘积，为克罗内克矩阵乘积，为ris相移幅度矩阵，为矩阵向量化性质，其中，a,b,c表示矩阵，vec(·)表示矩阵向量化算子，上标t表示矩阵转置，设置结合克罗内克矩阵乘积的混合乘积特性其中，a,b,c,d表示矩阵，将级联信道估计问题转化为稀疏信号恢复问题，

20、向量化处理后的接收信号方程为：

21、

22、其中，为感知矩阵，n为高斯噪声，x＝vec(k)为要恢复的信道增益稀疏信号。

23、进一步地，步骤s301中，对于第l个导频矩阵，l＝1,…,l，得到相应的接收信号向量yl，且接收信号在采样时隙中是独立的；为稀疏向量x设置先验条件，即假设稀疏信号xl是均值为0，协方差为φ的循环对称复高斯向量，将接收信号方程在l个导频下组成测量向量方程y＝ax+n；

24、所述稀疏信号的先验分布表达式如下：

25、

26、其中，yl为接收信号，xl为稀疏信号，σ2为噪声功率，i为单位阵，cn为高斯分布。

27、进一步地，步骤s302中，所述证据函数的表达式如下：

28、

29、其中，p(y)为证据函数，p(y|x)为先验分布，p(x)为稀疏信号的先验条件，∑y为证据函数协方差矩阵；对接收信号的似然函数进行证据最大化处理，采用第二类最大似然估计方法估计x；由于x的先验分布服从高斯分布，证据函数p(y)也服从高斯分布，得到证据函数的协方差矩阵∑y＝aγah+σ2i，其中，上标h表示共轭转置，a是感知矩阵，σ2是噪声功率，γ是稀疏信号x的协方差矩阵，i为单位矩阵。

30、进一步地，稀疏信号的先验条件p(x)包括均值为0，协方差为φ的循环对称复高斯向量。

31、进一步地，步骤s303中，所述证据函数的对数转换表达式如下：

32、

33、其中，∑l为第l个导频矩阵的协方差矩阵，|·|表示行列式，上标-1表示矩阵求逆，得到超参数γ的估计优化方程表达式如下：

34、

35、其中，为超参数估计，argmin{·}表示最小化，tr(·)表示矩阵的迹。

36、进一步地，步骤s304中，所述超参数估计表达式的求导表达式如下：

37、

38、其中，alc为感知矩阵的第l列向量；

39、根据上述求导结果，改进稀疏贝叶斯算法的超参数固定点更新迭代方程的表达式如下：

40、

41、其中，γnew和γold为两次相邻的超参数估计值，a为感知矩阵的列向量，b为收敛速度控制参数；

42、噪声功率σ2的固定点更新方程通过对数证据函数对σ2的偏导数得到，其表达式为：

43、

44、其中r为基站端天线数量，am为由整数元素集合m索引的a矩阵的c列组成，集合m指示稀疏向量x的稀疏项位置，对m的估计根据γ参数的估计得到，为矩阵am的伪逆矩阵，in为单位阵。

45、进一步地，步骤s305中，通过两次相邻的超参数估计值的l2范数差值和迭代次数，判断是否停止迭代。

46、本发明还提供一种计算机可读存储介质，其上存储有计算机程序，所述程序被处理器执行时实现上述方法。

47、与现有技术相比，本发明具有以下有益效果：

48、1、本发明建立可重构智能表面辅助的多输入多输出通信系统模型，获得级联信道的矩阵表示；然后通过矩阵向量化特性和克罗内克乘积性质对所述的级联信道的矩阵表示进行变换，得到接收信号的向量化表示；最后基于所述的接收信号的向量化表示，使用改进稀疏贝叶斯算法进行级联信道估计，其中，改进稀疏贝叶斯算法中，基于超参数估计表达式的微分结果构建超参数固定点更新迭代方程，可以在每一次迭代中逐渐逼近最优超参数值，更加精确地找到最优的超参数，避免因为搜索范围不够大而漏掉最优解的情况，进而可以提高级联信道估计精度。

49、2、本发明在计算证据函数时，引入了一个稀疏向量的先验条件，可以避免出现过学习现象，具有较高的泛化性。