一种基于信息新鲜度的多小区缓存更新方法

本发明属于边缘缓存，尤其涉及一种基于信息新鲜度的多小区缓存更新方法。

背景技术：

1、在云计算和物联网技术的飞速发展下，互联网视频、游戏和移动应用等高带宽、低延迟、高并发的应用呈现爆炸式增长，用户对于网络质量和响应速度的要求越来越高。在这种背景下，边缘缓存逐渐成为提高网络性能和用户体验的有效手段。边缘缓存是指将数据缓存到网络边缘节点，使得用户可以更快速地获取所需的内容，减少对服务器的请求并节约带宽资源。边缘缓存将计算和存储的负载分散到网络边缘，用户可以就近获取内容而不必经过远端的源站，与中心化缓存相比，显著降低了网络延迟，提高了用户访问速度和响应时间。

2、尽管边缘缓存能够满足一些用户的请求，但缓存基站的容量通常较小，不能够缓存所有的内容。此外，边缘缓存技术会使得缓存中存储的文件的新鲜度相对传统模式的较低。缓存什么样的内容以及如何有效地更新缓存内容同时保证内容的新鲜度成为一个挑战。因此，需要制定一个有效的缓存更新策略来缓存热门新鲜内容，以此尽可能地低成本满足更多的用户请求。

3、现有的缓存策略在场景方面大多由特定的单个边缘缓存服务器来满足用户的请求，未充分利用到附近的网络资源，通常多个小区基站之间存在重叠区域，位于重叠区域的用户可以有多个候选服务器的选择；在缓存模型方面，大多研究忽略了从基站下载内容的成本，且新鲜度的时变性也很少被考虑到；在缓存方法方面，由于边缘缓存问题通常为大规模优化问题，在缓存方法上还存在效率低下和结果精度不高等问题。为此，需要一种基于信息新鲜度的多小区缓存更新策略，实现缓存内容下载更新等成本与信息新鲜度时变性带来的缓存性能问题的权衡，以此以低成本来高效地满足更多的用户请求。

技术实现思路

1、本发明目的在于提供一种基于信息新鲜度的多小区缓存更新方法，以解决上述的技术问题。

2、针对多小区重叠区域网络资源利用率低、新鲜度时变性以及大规模优化问题求解复杂性等问题，本发明提供了一种基于信息新鲜度的多小区缓存更新策略，联合考虑内容下载成本、缓存内容更新成本和信息新鲜度下降带来的过时惩罚成本，建立多小区具有重叠区域的缓存更新模型，采用改进的分支定价算法实现在保证信息新鲜度的同时以低成本满足更多的用户下载请求。

3、为了达到发明目的，本发明公开了一种基于信息新鲜度的多小区缓存更新策略，具体步骤包括：

4、一种基于信息新鲜度的多小区缓存更新方法，包括以下步骤：

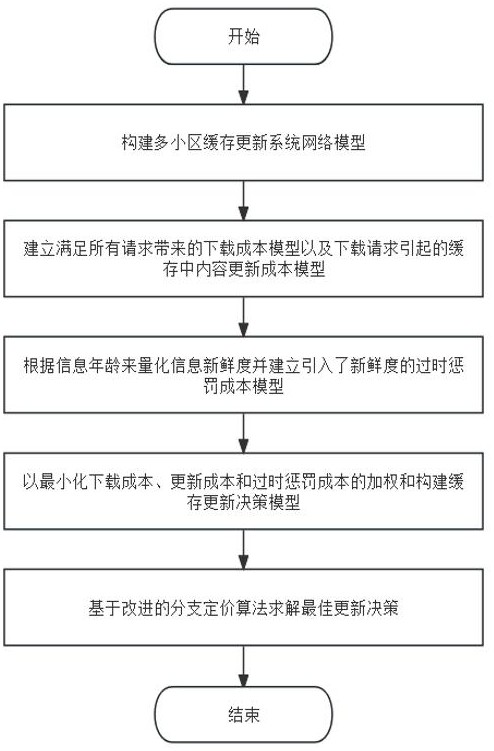
5、s1：构建多小区缓存更新系统网络模型；

6、s2：建立满足所有请求带来的下载成本模型以及下载请求引起的缓存中内容更新成本模型；

7、s3：根据信息年龄来量化信息新鲜度并建立引入了新鲜度的过时惩罚成本模型；

8、s4：以最小化下载成本、更新成本和过时惩罚成本的加权和构建缓存更新决策模型；

9、s5：基于改进的分支定价算法求解最佳更新决策。

10、进一步的，所述s1具体包括：系统由云服务器n和h个小区组成，每个小区中都有一个缓存服务器，缓存服务器集合用h＝{1,2,…,h}表示，小区之间存在重叠区域，边缘缓存节点以低成本的方式将文件发送给用户，用ch表示从缓存向用户提供文件的单元成本，通过缓存满足用户内容请求，缓存服务器的缓存容量限制记为vh，云服务器存储有f＝{1,2,…,f}个文件，通过云服务器直接将文件发送给用户，文件优先通过缓存发送。

11、进一步的，所述s1一组时隙t＝{1,2,…,t}组成的调度时域，用r＝{1,2,…,r}(r＝rm∪rs)表示请求集合，请求分为两种类型：

12、多选择请求：位于重叠区域的用户发起的请求，有多个候选缓存服务器供其选择，用rm表示多选择请求集合；

13、单选择请求：只有一个缓存服务器可满足的剩余请求，用rs表示单选择请求集合；

14、每个请求r由一个四元组fr，or，dr，hr组成，其中：fr表示r请求的内容，or表示请求r的时隙，dr表示满足请求r的截止时间，hr表示请求r的候选服务器集合；

15、对于一个请求，如果请求的内容在截止时间之前都没有缓存在候选缓存服务器中，则该内容将从云服务器下载。

16、进一步的，所述s2具体包括：

17、s2.1：计算满足所有请求带来的下载成本记为cd，即：

18、

19、式中，lfr表示内容fr的大小，cn和ch分别表示从云服务器和缓存服务器提供请求内容的单元成本，cn>ch，zrha是一个二进制变量，当且仅当请求r被缓存服务器h满足且具有a的aoi时为1，否则为0，当请求不被缓存服务器满足时，式子右边为0，即下载成本为从云服务器下载的成本；当请求被缓存满足时，式子左边为0，即下载成本为从缓存下载的成本。

20、一个请求最多需要服务器响应一次，所以有：

21、

22、此外，只有当缓存服务器h在时隙t∈{or,…,dr}中存在aoi为a∈{0,1,…,dr-1}的内容fr时，请求r才能被缓存服务器满足，定义二进制变量yhtfa，当且仅当内容f在t时隙缓存在服务器h中且具有a的aoi时为1，否则为0，则有：

23、

24、s2.2：计算缓存内容更新成本记为cu，即：

25、cu＝∑h∈h∑t∈t∑f∈flf(cn-ch)yhtf0  (4)

26、式中，lf表示内容f的大小，cn-ch表示缓存服务器从云服务器下载内容的单位成本，二进制变量yhtfa，当且仅当内容f在t时隙缓存在服务器h中且具有a的aoi时为1，否则为0，yhtf0为1时表示缓存服务器h在t时隙更新内容f，刚下载更新内容的aoi为0；

27、定义二进制变量xhtf，如果缓存服务器h在时隙t缓存内容f则等于1，则有：

28、

29、进一步的，所述s3：具体包括：

30、s3.1：存储在缓存中的内容的新鲜度会随着时隙的增加而降低，新鲜度用信息年龄aoi来量化，将信息年龄定义为缓存中的一个文件从当前时隙与最近一次更新时隙之间的时间之差，记为a，假设缓存服务器在时隙t刚刚下载内容f，当在时隙为t′时，内容的信息年龄a的表达式计算如下所示：

31、a＝t′-t  (6)

32、s3.2：定义内容f过时的惩罚成本，将其定义为内容的信息年龄与其大小的乘积，记为pf(a)，即：

33、pf(a)＝a×lf  (7)

34、s3.3：进一步定义系统内容新鲜度下降带来的过时惩罚成本ca，即：

35、进一步的，所述s4具体包括：

36、权衡下载成本、更新成本以及新鲜度下降带来的过时惩罚成本，目标是保证内容新鲜度同时降低网络负载，使系统总成本最小，构建优化问题，即：

37、

38、s.t.yh(t-1)f(a-1)≥yhtfa,h∈h,t∈t,f∈f,a∈{1,2,…,t-1}  (9a)

39、

40、

41、

42、∑f∈flfxhtf≤vh,h∈h,t∈t。  (9e)

43、进一步的，所述s5具体包括：

44、s5.1：重新简化表述原目标优化问题并松弛，定义决策对(xhf，yhf)表示节点对文件在所有时隙的缓存和更新决策，即：xhf＝[xh1f,xh2f,…,xhtf]′，yhf＝[yh1f0,yh2f0,…,yhtf(t-1)]′，一组决策对在每个时隙有三种可能：(0，0)、(1，0)和(1，1)，t个时隙共有3t个二进制变量的可能组合，包含了内容f的所有缓存可能，定义索引集k＝[1,2,…,3t]表示所有的决策(xhf，yhf)对组合，每个文件内容的一种在所有时隙内的(xhf，yhf)对组合为该索引集k中对应的一列，k∈k表示一种可能的解，定义二进制变量whfk当且仅当缓存服务器h及内容f的决策选择了第k列时为1，否则为0，对于任意给定的列，原目标优化问题的部分成本是确定的，包括有更新成本及服务器的单选择请求的下载成本和过时惩罚成本，使用chfk表示确定的成本之和，未知的成本大小与z变量有关，也就是多选择请求的下载成本和过时惩罚成本，分别用cdm和cam表示，则原目标优化问题重新表述并松弛为：

45、

46、

47、

48、(10c)

49、∑f∈flfxhfwhfk≤vh,h∈h,t∈t(10d)

50、∑k∈kwhfk＝1,h∈h,f∈f(10e)

51、式中，二进制变量brhak表示当且仅当缓存服务器h和内容f的第k列能够以aoi a满足请求r时为1；

52、s5.2：初始化分支定界树，生成根节点，在分支定界树上选取一个节点，选择每个决策变量的中间值作为初始值，这些取值则是当前子问题的一个可行解；

53、s5.3：初始化rmp并求解rmp的线性松弛问题，得到对偶变量值，通过公式(10)问题的k矩阵的子矩阵k′构造rmp问题，设置较小的k′能快速得到初始解；

54、s5.4：根据对偶变量值求解子问题，在rmp最优处，用分别表示(10c)、(10d)和(10e)对应的最优对偶变量，则对于任意缓存服务器h内容f，第k列的缩减成本为：

55、

56、则子问题可表述为：

57、

58、

59、yh(t-1)f(a-1)≥yhtfa,h∈h,t∈t,f∈f,a∈{1,2,…,t-1}(12b)

60、

61、通过最短路径迪杰斯特拉算法求解该子问题，找到从起点到终点的最短路径的过程等效于求解子问题；

62、s5.5：根据子问题的最优解判断是否向rmp中添加新的列，当子问题的最优解小于0时表示子问题检验的未被考虑的变量对原问题有改进，有改进就将变量的相关系数的列加入到rmp问题的系数矩阵中；

63、s5.6：根据rmp的解进行分支、剪支操作，判断rmp的解是否优于上界，当rmp的解差于上界时直接删除当前节点，进一步判断rmp的解是否为整数，当解优于上界且为整数时更新上界，否则继续进行分支；

64、s5.7：重复上述过程直到找到最优解，当分支定界搜索树为空时停止迭代，

65、算法结束。

66、本发明的一种基于信息新鲜度的多小区缓存更新方法具有以下优点：

67、本发明构建了一个在具有重叠区域的多小区场景下优化新鲜度和缓存成本的缓存更新模型，将基站下载更新内容成本和新鲜度过时惩罚成本考虑到系统总成本中，更具备实用性。

68、本发明充分利用到重叠区域的网络资源，在保证信息新鲜度的同时以低成本满足用户下载请求，提高了网络资源利用率，提升了缓存系统性能。

69、本发明设计了基于改进的分支定价算法来实现大规模的缓存更新优化问题，有效权衡系统成本与新鲜度性能，有效解决了问题规模大、子问题求解效率低下以及求解结果的精度问题，提高了算法的效率和准确性。