一种基于分布凸优化方法的多能源管控方法及系统

本发明涉及能源管理控制，具体而言，涉及一种基于分布凸优化方法的多能源管控方法及系统。

背景技术：

1、利用清洁能源的智能电网，集传统发电模块、清洁能源发电模块、用户需求模块、先进管理和智能控制技术于一体，相比于传统电网更加清洁、可靠、安全、高效和可持续，清洁能源智能电网配备智能可控电气设备和先进的通信网络，使分布式控制和分布式能源管理成为可能。与此同时，发电模块数量的增加也导致了发电模块控制器设计的复杂性。

2、在现有技术中，提出了一种自适应分布式算法，该方法将多节点分布式优化问题转化为共识条件下的一般形式，然后通过一个收敛到最优解的控制器来解决分布式最优共识问题，但其不足是，该方法从元件通信节点的角度建立的，这意味着该算法需要从其相邻元件中获得更多的通信信息，增加了通信通道的负担，导致通信成本昂贵。或从控制角度出发，提出了求解无向连通图上的集中式优化算法和分布式优化算法，并对这类算法进行了改进。但是其问题在于：已有的关于控制器增益选择的结果过分依赖于系统的整体信息，这对于一个复杂的网络系统来说尤其困难，并且它们可能会不可行。

技术实现思路

1、本发明要解决的技术问题是：

2、为了解决现有能源管理或从元件通信节点出发，增加了通信通道负担，导致成本高昂；或从控制角度出发，过分依赖系统整体信息，对于复杂网络难以执行的问题。

3、本发明为解决上述技术问题所采用的技术方案：

4、本发明提供了一种基于分布凸优化方法的多能源管控方法，包括以下步骤：

5、s100、构建包含传统发电元件、清洁能源发电元件和用户需求元件的多能源管控优化问题模型，包括传统发电单元费用的构建、清洁能源发电单元费用的构建、用户对能源需求满意度的构建，在考虑到微增输电损耗后对整个多能源管控优化问题进行建模；

6、s200、根据步骤s100中的多能源管控优化问题模型以及拉格朗日对偶问题的解存在性定理设计将优化问题转化为凸优化问题的充分条件；

7、s300、根据初始-对偶鞍点理论获取求解凸优化问题的迭代序列，包括根据步骤s200转化后的凸优化模型进行求解算法的设计，以使得从初值开始的解轨迹能够收敛到优化问题的全局最优解，实现原始分布凸优化问题的求解。

8、进一步地，在步骤s100中，具体包括：

9、将多能管理问题转化成一个如下所示的凸优化问题：

10、

11、其中，fi(xi(t))为凸性能指标函数，xi(t)为系统调控参数，n为能源单元数量，m为时间序列长度，g(xi(t))≤0代表不等式约束，h(xi(t))＝0代表等式约束，xi(t)∈ωi(t)代表优化变量约束；

12、设微电网网络模型中含有n个传统发电单元，q个清洁能源发电单元，以及m个需求单元，定义：

13、p1,g,…,pn,g为传统发电单元的发电功率；

14、p1,r,…,pq,r为清洁能源发电单元的发电功率；

15、p1,d,…,pm,d为用户单元的需求功率；

16、传统发电单元费用构建如下：

17、

18、清洁能源发电单元费用构建如下：

19、

20、其中，αi,g、bi,g、ci,g、αj,r、bj,r和cj,r均为发电费用函数固有参数，是能源网络中传统发电单元所在序号集合，是能源网络中清洁能源发电单元所在序号集合；

21、根据每个发电单元的微增输电损耗，输电损耗pi,l可表示为以下二次函数：

22、

23、

24、其中，li,g和lj,g分别为传统发电单元的损耗系数和清洁能源发电单元的损耗系数，且满足0≤li,g<ai,g，0≤lj,r<aj,r；

25、对于能源需求单元k，定义用户对能源需求的满意度为：

26、

27、其中，αk和βk均为预定义参数；是能源网络中用户单元所在序号集合；

28、整个多能源管控优化问题建模如下：

29、

30、

31、

32、

33、其中，为传统发电单元的最小发电功率，为传统发电单元的最大发电功率；为清洁能源发电单元的最小发电功率，为清洁能源发电单元的最大发电功率；为用户单元的最小需求功率，为用户单元的最大需求功率。

34、进一步地，在电网中，发电量应始终满足总需求功率的要求；因此，设总发电量满足需求要求，即有：

35、

36、进一步地，在步骤s200中，具体包括：

37、对于步骤s100中的优化建模问题，将其中的非凸约束进行凸化，原优化建模问题可转化为如下凸优化问题：

38、

39、

40、

41、

42、原优化建模问题的最优值和对偶问题的最优值具有强对偶性，转换问题的拉格朗日函数为：

43、

44、

45、其中，p＝[p1,p2,…,pn+q+m]t，p为优化变量向量，μ、π和λ均为拉格朗日乘数；代表

46、凸优化问题的最优解p*满足kkt条件：

47、

48、

49、

50、

51、

52、

53、当时，λ＝0成立；

54、当且则下面两式成立：

55、

56、

57、因此，

58、同理，可得到：

59、

60、因此，给出保证转化后的凸优化问题与原问题具有相同解的充分条件：

61、

62、对于转换问题的最优解，满足：

63、

64、进一步地，在步骤s300中，具体包括：

65、由于凸优化问题不包含等式约束，令n＝n+q+m，则可将原问题写成紧凑形式：

66、

67、首先利用一个拉格朗日鞍点表征，问题等价于：

68、

69、相关的拉格朗日对偶问题为：

70、

71、其中，拉格朗日对偶函数定义为拉格朗日对偶问题的对偶最优值用d*表示，拉格朗日对偶最优点的集合用表示；根据slater条件，强对偶成立；原问题和拉格朗日对偶问题的最优解可以被表征为拉格朗日函数的鞍点；为实数合集；为i个能源单元的功率约束；

72、为找到的一个超紧凑集合，包括，

73、为每个能源元件i定义以下基本问题：

74、

75、相应的对偶问题为：

76、

77、其中，对偶函数lagri(p,λ)为第i个能源元件的拉格朗日函数；对应的对偶最优值表示为

78、lagr可分解为局部拉格朗日函数的和，即：

79、

80、定义函数γ:为如果p是slater向量，则γ(p)>0；选择任意一个slater向量并令有：

81、

82、定义函数w:由于对偶性质，对于任意有fi(p)≥qi(λ)；因为因此对于任意都有取任意则下列集合就可以通过θi定义：

83、

84、因为有：

85、

86、又因为所以：

87、

88、因此，对于任意有

89、定义紧凑凸集

90、进一步地，在步骤s300中还包括：

91、首先，每个能量元件i选择一个共同的slater向量和一个共同的然后能量元件i利用θi通过最大共识算法计算出集合其中θi>0；能量元件i可选择任意初始状态和yi(1)＝nfi(pi(0))，在每一个t≥0，每一个能量元件i根据下式生成三个迭代结果pi(t+1)、λi(t+1)和yi(t+1)：

92、

93、

94、

95、

96、

97、yi(t+1)＝ci,y(t)+n[fi(pi(t))-fi(pi(t)-1))]

98、其中分别为集合和上的投影算子，标量为非负凸组合权重，标量ξ(t)>0为步长，t为时间；

99、定义lagri,λ(p):lagri,p(λ):定义为函数的子梯度算子，任意函数f:在处的子梯度有性质，对于有然后有

100、在每个时间t，每个能量元件i都保持对拉格朗日函数鞍点的估计(pi(t),λi(t))和对最优值p*的估计yi(t)；

101、为了产生pi(t+1)，能量元件i的值取其估计值pi(t)和与其相邻的能量元件在时间t上的估计值进行凸组合ci,p(t)，使次梯度步骤最小化局部拉格朗日函数lagri(p,λ)，并在局部约束上进行初始投影；

102、能量元件i通过将其估计值pi(t)与相邻节点在时间t的估计值进行凸组合ci,x(t)，并通过一步跟踪局部目标函数fi的变化来生成估计pi(t+1)；

103、通过迭代，pi(t+1)收敛到分布式凸优化问题的最优解，实现能源系统最优效益的发电与需求功率分布求解。

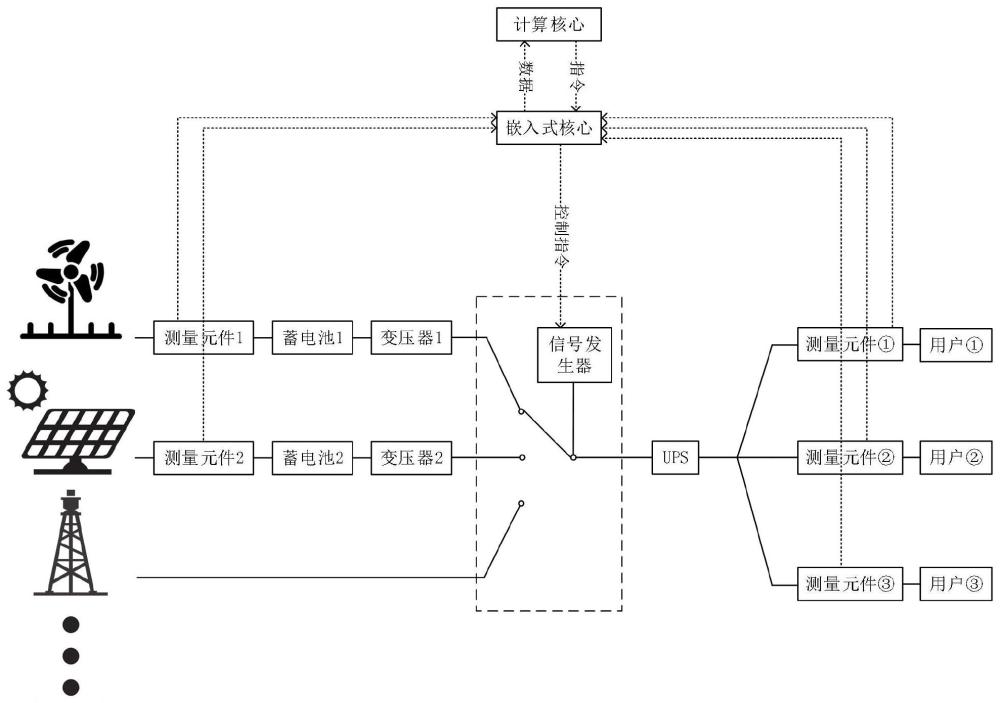
104、一种基于分布凸优化方法的多能源管控系统，包括变压器、能源控制模块与控制外电路，

105、所述变压器，用于传统能源和清洁能源的输出调配至同一状态，便于后续搭配能源控制模块实现能源管理；

106、所述能源控制模块，包括能源切换器和信号发生器，用于在能源切换器接收到信号后利用信号发生器实现能源的对应切换；

107、所述控制外电路，用于获取分布式能源的测量数据、对能源数据进行分析、优化并决策以及向能源控制模块发送控制信号。

108、进一步地，所述控制外电路包括嵌入式核心和计算机核心，所述嵌入式核心用于对能源数据的接收与预处理，所述计算机核心用于对能源数据进行分析与优化，并产生决策后，通过无线或有线通讯，向嵌入式核心发送控制信号。

109、进一步地，所述嵌入式核心收到测量元件的离散数据后，先通过一个离散滤波器，去除环境噪声；将获得的电气参数通过计算整理，得到清洁能源的发电功率与各个用户的用电功率；然后将功率数据传给计算核心，带入优化方程计算，并根据优化结果进行决策，得到切换方案。

110、进一步地，还包括ups，所述ups内部设有蓄电池，用于应对紧急情况中的短暂供电。

111、相较于现有技术，本发明的有益效果是：

112、本发明一种基于分布凸优化方法的多能源管控方法及系统，构建包含传统发电元件、清洁能源发电元件和用户需求元件的多能源管控优化问题模型，根据多能源管控优化问题模型以及拉格朗日对偶问题的解存在性定理设计将优化问题转化为凸优化问题的充分条件，根据初始-对偶鞍点理论获取求解凸优化问题的迭代序列；本发明方法能够实现在存在大规模的传统发电单元、清洁能源发电单元和用户能源需求单元的能源系统中，解决从任意初始点开始的最优能源分布问题，实现大规模能源系统的成本和用户满意度的最优化，从而达到整能源系统总体经济效益的最大化，可应用于大型能源网络的效率控制以保证整体能源系统实现最大效益。