一种基于非负CP分解的高光谱图像压缩加密方法
- 国知局
- 2024-08-02 12:45:24
本发明涉及高光谱图像加密,尤其涉及一种基于非负cp分解的高光谱图像压缩加密方法。
背景技术:
1、高光谱成像作为光学遥感技术中的一个重要概念,一直是研究人员非常关注的话题。高光谱图像表示为三维数据立方体,以其丰富的光谱信息、高光谱分辨率和多波段整合特性为主要特点。高光谱图像不仅能从紫外到微波范围内的数百个连续波段中捕获精准的光谱信息,还可以整合多个波段的信息形成多维数据立方体,以提供更全面且更复杂的图像信息,适用于对复杂场景的深入分析。此外,高光谱图像还具有光谱分辨率高、数据量大以及可同时提供空间和光谱域信息等特点。近年来,高光谱图像已经在军事目标侦测、生物医学诊断、环境监测、地质矿产勘探、生态自然灾害与生态环境监测等领域被广泛应用。而高光谱图像作为军事和医疗领域的敏感信息,为防止其数据信息在传输、存储以及处理过程中被非法访问者恶意破坏或者篡改攻击,高光谱图像的信息安全问题变得尤为重要。尽管研究者目前已经提出许多基于光学变换的高光谱图像光学加密方案以保护其数据安全,但是由于高光谱图像存在波段多且数据量大的特点,导致高光谱图像的密文数据量远远超过了传统的灰度图像或彩色图像,增加了存储和传输的负担。因此,传统的加密技术无法在保护高光谱图像数据安全性的同时,实现快速高效的传输。所以,针对高光谱图像的存储和传输限制以及安全性需求,着力研究高光谱图像的压缩加密算法,实现其数据的快速安全传输,同时降低存储成本,并保护高光谱图像的安全性就变得尤为重要,不仅具有重要的学术价值,也是我国高光谱遥感领域面临的新机遇和挑战,同时还能推动我国信息安全领域的快速发展。
2、文献号为cn113660078a的中国专利申请《一种基于随机螺旋相位变换的高光谱图像加密方法》公开了一种高光谱图像加密方法为:将高光谱图像作为秘密数据,将其与随机螺旋相位一起作为回转器变换域内随机螺旋变换的输入函数,再利用新型置乱编码算法对螺旋变换的输出函数进行进一步处理,得到加密后的高光谱图像。该方法实现了密码系统更高的安全性,但由于该方法是对高光谱数据中的每个波段进行依次加密,因此高光谱图像大规模的密文数据量的存储和传输阻碍了该方法的实际应用。
3、文献号为cn103281534b的中国专利申请《一种高光谱图像压缩加密方法》公开的方法为:采用基于三维小波变换的分层数集合划分方法(3d set partitioning inhierarchical trees,3dspiht)对高光谱图像进行编码,且在编码的同时进行加密,通过logistic映射构造置乱表置乱初始化的不重要子集表lip,通过不断迭代chen's模型直到完成所有重要类型比特的加密,解密过程是加密的逆运算,通过不断更新chen's模型初始值来解密重要类型数据,逐步逼近原图像,最后再现原图像。该方法根据3dspiht编码方法的前向依赖性,在压缩的过程中有选择的实时加密重要类型数据,减少了图像的密文数据量,提高了图像传输和加密效率,并且增加了密码方法对明文的敏感性。但由于三维小波变换的特性,当选择压缩比过大时,解密得到的恢复图像将严重失真,所以该方法对高光谱图像的压缩效果有限,故密文数据的存储和传输问题仍未解决。
技术实现思路
1、针对上述现有技术的不足,本发明提出了一种基于非负cp分解的高光谱图像压缩加密方法,解决大规模的高光谱图像密文数据的存储和传输问题。
2、本发明提出的一种基于非负cp分解的高光谱图像压缩加密方法,该方法包括如下步骤:
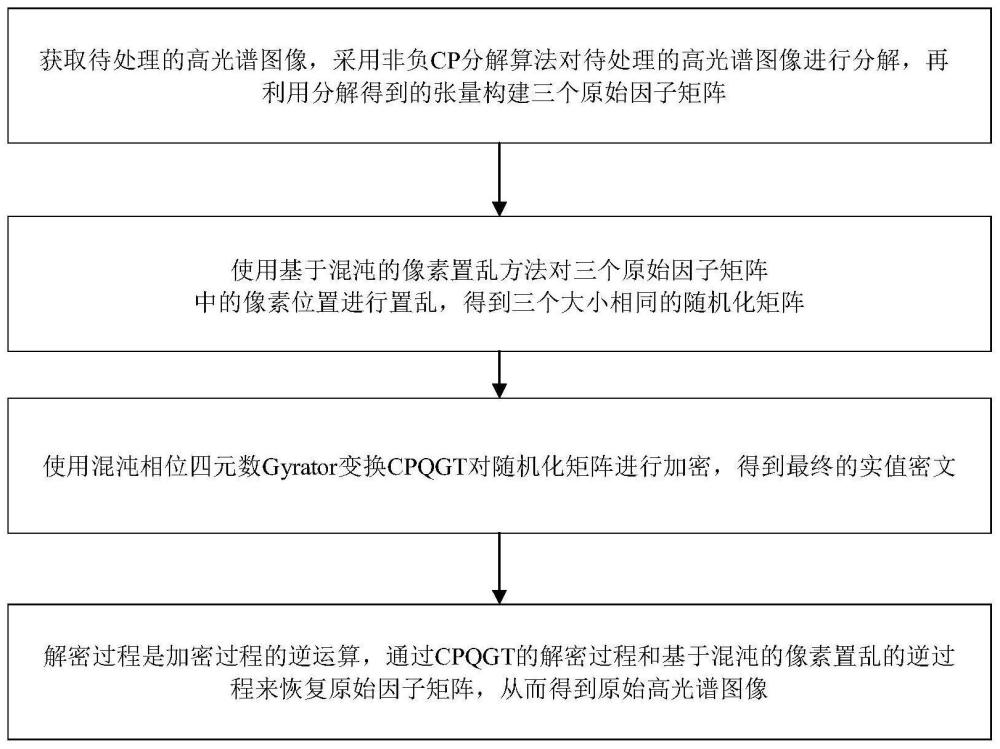
3、步骤1:获取待处理的高光谱图像,采用非负cp分解算法对待处理的高光谱图像进行分解,再利用分解得到的张量构建原始因子矩阵a、b和c;
4、步骤2:使用基于混沌的像素置乱方法对原始因子矩阵a、b和c中的像素位置进行置乱,得到大小相同的随机化矩阵a′、b′和c′;
5、步骤3:使用混沌相位四元数gyrator变换cpqgt对随机化矩阵a′、b′和c′进行加密,得到最终的实值密文;
6、步骤4:解密过程是加密过程的逆运算,通过cpqgt的解密过程和基于混沌的像素置乱的逆过程来恢复原始因子矩阵,从而得到原始高光谱图像;
7、所述步骤1进一步包括:
8、步骤1.1:获取待处理的高光谱图像,并将待处理的高光谱图像表示为一个三阶张量且所述高光谱图像的大小为i×j×k,其中i为高度;j为宽度;k为光谱通道的维度;为张量尺寸;
9、步骤1.2:对待处理的高光谱图像进行非负cp分解,得到r组张量之和;r为三阶张量的秩;每组张量均包括i、j和k三个维度上的秩为1的张量ar、br和cr;其中r表示第r组张量,且r∈[1,r];
10、步骤1.3:分别利用张量ar、br和cr构建i、j和k三个维度上的原始因子矩阵a、b和c;
11、所述原始因子矩阵a、b和c分别为:
12、
13、
14、
15、其中a表示i维度上的原始因子矩阵,大小为i×r;其中a1、a2和ar分别表示原始因子矩阵a中的第1个张量、第2个张量和第r个张量;b表示i维度上的原始因子矩阵,大小为j×r;其中b1、b2和br分别表示原始因子矩阵b中的第1个张量、第2个张量和第r个张量;c表示k维度上的原始因子矩阵,大小为k×r;其中c1、c2和cr分别表示原始因子矩阵c中的第1个张量、第2个张量和第r个张量;
16、所述步骤2进一步包括:
17、步骤2.1:定义logistic-tent混沌映射;
18、步骤2.2:将原始因子矩阵a,b,c纵向拼接,得到大小为(i+j+k)×r的2d图像p,计算图像p的高度i+j+k是否是3的倍数;如果不是,则在图像p下方填充n行零像素,使填充后的图像高度i+j+k+n为3的倍数;若是,则n的取值为0;其中n为所有满足i+j+k+n为3的倍数的取值中的最小值;
19、步骤2.3:采用logistic-tent混沌映射生成混沌序列x,将x中的元素按照升序或降序进行排序,得到新的混沌序列x′,利用新的混沌序列x′与混沌序列x建立图像像素置乱的规则,记为x′=x(w),得到排列索引w;
20、步骤2.4:将填充后的大小为(i+j+k+n)×r的2d图像中的像素通过逐行取值转换为一维序列y={yj,j=ty+1,ty+2,...,ty+(i+j+k+n)×r},其中yj表示y中的第j个元素;ty为截断位置;使用排列索引w将序列y重新排序为新的一维序列y′,记为y′=y(w);将新的一维序列y′转换为置乱后的图像p′,再对置乱后的图像p′平均划分为三个大小相同的随机化矩阵a′、b′和c′;所述随机化矩阵a′、b′和c′的大小均为
21、所述logistic-tent混沌映射的定义方程为:
22、
23、其中xn+1表示logistic-tent混沌映射中第n+1次迭代的结果;xn表示logistic-tent混沌映射中第n次迭代的结果;mod为取模运算符;
24、所述采用logistic-tent混沌映射生成混沌序列x的方法为:给定logistic-tent混沌映射的初始值x0、函数参数rx和截断位置tx,采用logistic-tent混沌映射生成长度为(i+j+k+n)×r+tx的随机logistic-tent混沌序列{xi},其中xi表示随机logistic-tent混沌序列中的第i个元素;舍弃随机logistic-tent混沌序列{xi}中前tx个元素,得到混沌序列x={xi,i=tx+1,tx+2,...,tx+(i+j+k+n)×r};
25、所述步骤3进一步包括:
26、步骤3.1:采用四元数矩阵形式将随机化矩阵a′、b′和c′表示为cpqgt的输入函数的分量;
27、步骤3.2:定义logistic-tent混沌映射的初始值y0、函数参数ry和截断位置ty各自与cpqgt的旋转角度α和β之间的映射关系,并利用定义的映射关系和给定的cpqgt的旋转角度α和β计算logistic-tent混沌映射的初始值y0、函数参数ry和截断位置ty,根据logistic-tent混沌映射利用得到的y0、ry和ty生成一维混沌序列再将一维混沌序列转换为2d矩阵y(x,y);其中w*h表示2d矩阵y(x,y)的大小;
28、步骤3.3:将2d矩阵y(x,y)作为相位,构建logistic-tent混沌映射生成的混沌相位掩膜cpm;
29、步骤3.4:对cpqgt的输入函数使用混沌相位四元数gyrator变换,得到实值密文函数g(u,v),进而利用实值密文函数g(u,v)得到最终的实值密文;
30、所述实值密文函数g(u,v)为:
31、
32、其中u和v表示混沌相位四元数gyrator变换中输出平面得到的坐标;表示旋转角度为α、β的cpqgt;表示旋转角度为α的四元数gyrator变换,表示旋转角度为β的逆四元数gyrator变换。
33、采用上述技术方案所产生的有益效果在于:
34、本发明方法提出了一种基于非负cp分解和混沌相位四元数gyrator变换的高光谱图像压缩加密算法,与以往的高光谱图像加密方案相比,本发明方法不仅可以实现良好的加密安全性,而且可以显著降低高光谱图像加密时的计算复杂度和密文数据量,解决了高光谱图像密文数据的存储和传输问题。此外,本发明方法还确保了输出密文为实值密文而非复值的,有利于输出密文在实际应用中的传输。
本文地址:https://www.jishuxx.com/zhuanli/20240802/237662.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 YYfuon@163.com 举报,一经查实,本站将立刻删除。