基于博弈论的海上边缘计算网络任务卸载方法

本发明涉及海上无线通信网络，尤其涉及一种基于博弈论的海上边缘计算网络任务卸载方法。

背景技术：

1、现有的边缘计算相关研究通常以陆上环境为主，针对海上的边缘计算技术相关研究稀缺，有必要开发更高效的系统架构和边缘计算计算解决方案。目前对于通信和计算资源有限的海上设备而言，移动边缘计算(mec)展现出了巨大的潜力，能有效解决海洋设备的数据采集和计算能力受限的问题，其通过将计算任务卸载到具备强大计算能力的边缘计算服务器，可以显著提升数据处理速度，并有效分散计算负担。然而，当众多用户同时选择卸载任务时，边缘计算服务器可能会面临过载挑战，导致响应速度显著下降，且没能同时考虑用户、服务器端的利益。因此，研究海洋用户的卸载策略在移动边缘计算中显得尤为关键。

技术实现思路

1、本发明提供一种基于博弈论的海上边缘计算网络任务卸载方法，以克服上述技术问题。

2、为了实现上述目的，本发明的技术方案是：

3、一种基于博弈论的海上边缘计算网络任务卸载方法，包括以下步骤：

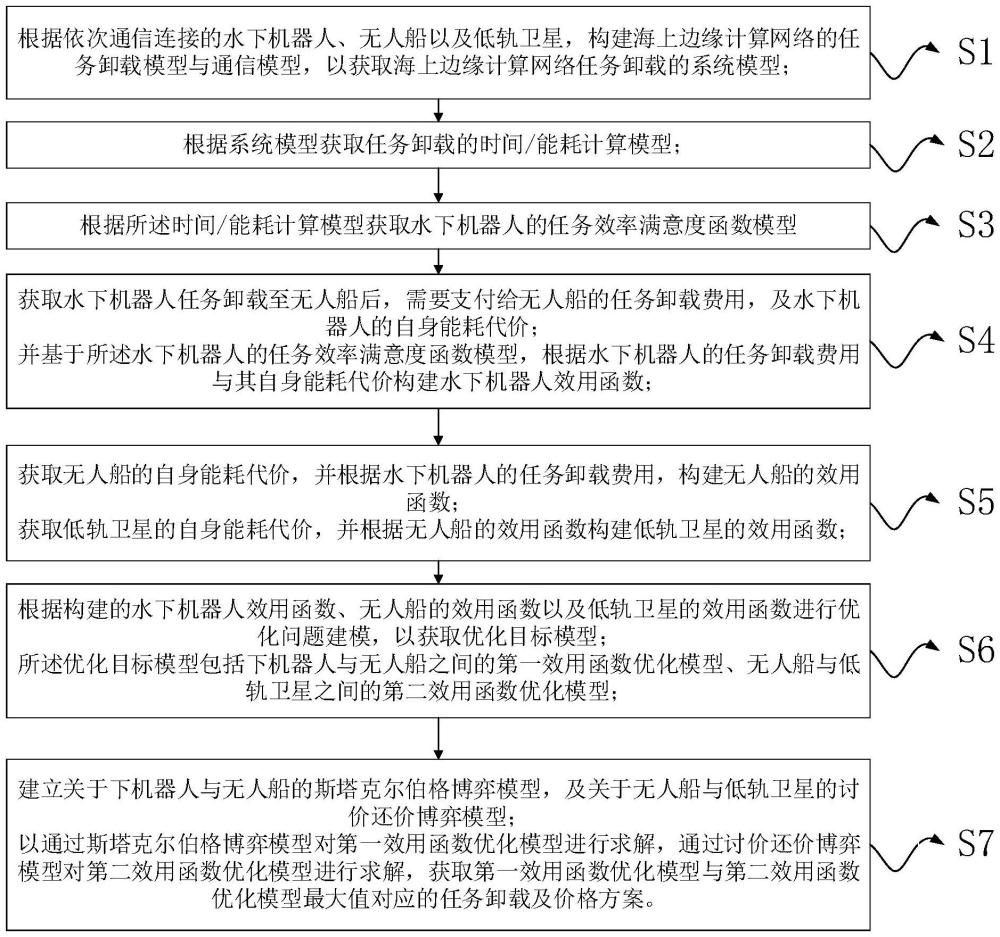
4、s1：根据依次通信连接的水下机器人、无人船以及低轨卫星，构建海上边缘计算网络的任务卸载模型与通信模型，以获取海上边缘计算网络任务卸载的系统模型；

5、s2：根据系统模型获取任务卸载的时间/能耗计算模型；

6、s3：根据所述时间/能耗计算模型获取水下机器人的任务效率满意度函数模型；

7、s4：获取水下机器人任务卸载至无人船后，需要支付给无人船的任务卸载费用，及水下机器人的自身能耗代价；

8、并基于所述水下机器人的任务效率满意度函数模型，根据水下机器人的任务卸载费用与其自身能耗代价构建水下机器人效用函数；

9、s5：获取无人船的自身能耗代价，并根据水下机器人的任务卸载费用，构建无人船的效用函数；

10、获取低轨卫星的自身能耗代价，并根据无人船的效用函数构建低轨卫星的效用函数；

11、s6：根据构建的水下机器人效用函数、无人船的效用函数以及低轨卫星的效用函数进行优化问题建模，以获取优化目标模型；

12、所述优化目标模型包括下机器人与无人船之间的第一效用函数优化模型、无人船与低轨卫星之间的第二效用函数优化模型；

13、s7：建立关于水下机器人与无人船的斯塔克尔伯格博弈模型，及关于无人船与低轨卫星的讨价还价博弈模型；

14、以通过斯塔克尔伯格博弈模型对第一效用函数优化模型进行求解，通过讨价还价博弈模型对第二效用函数优化模型进行求解，获取第一效用函数优化模型与第二效用函数优化模型最大值对应的任务卸载及价格方案。

15、进一步的，s1中获取海上边缘计算网络任务卸载的系统模型，包括以下步骤：

16、s11：定义用于负责监测海洋环境与收集海洋数据的水下任务的水下机器人集合i且i＝{1，2，…，i}；

17、用于为水下机器人提供边缘计算服务的无人船集合m且m＝{1，2，…，m}；

18、以及用于将无人船无法承担的计算任务卸载至云服务器处理的低轨卫星集合n且n＝{1，2，…，n}；

19、s12：采用三维笛卡尔坐标系将第i个水下机器人的坐标表示为vi＝(xi,yi,zi)，将第m个无人船的坐标表示为vm＝(xm,ym,zm)；其中xi,yi,zi分别表示第i个水下机器人在三维笛卡尔坐标系下的位置横坐标、纵坐标以及垂向坐标；xm,ym,zm分别表示第m个无人船在三维笛卡尔坐标系下的位置横坐标、纵坐标以及垂向坐标；

20、则所述水下机器人与无人船之间的距离di,m表示为

21、

22、所述低轨卫星与无人船之间的距离dm,n表示为

23、

24、式中：re表示地球半径；h表示卫星到地球的距离；φm,n表示无人船和卫星之间的地心角；

25、s13：构建海上边缘计算网络的任务卸载模型，具体为

26、将水下机器人i的网络任务表示为其中表示该网络任务数据量的大小；表示完成该网络任务需要的计算资源；

27、定义水下机器人i到无人船m的任务卸载率为ai,m，且0≤ai,m≤1；

28、则通过水下机器人i计算的任务量表示为

29、定义无人船m到低轨卫星的任务卸载率为bm,n，且0≤bm,n≤1；

30、则通过无人船m计算的任务量表示为

31、s14：所述水下机器人与无人船之间采用noma进行通信，并基于香农定理根据水下机器人与无人船之间的距离di,m与任务卸载模型，获取水下机器人与无人船的通信模型，其表达式为

32、

33、式中：ri表示水下机器人i与无人船m之间的通信传输速率；wi表示信道带宽；pi表示发送功率；gi表示信道增益；h(di,m,f)表示水声信号的衰落因子，即水下机器人i与无人船m之间距离的函数；表示水下机器人i与无人船m之间任务卸载的传输时间；表示水下机器人i与无人船m之间任务卸载的传输能耗；

34、s15：所述无人船与低轨卫星之间采用fdma进行通信，并基于香农定理根据低轨卫星与无人船之间的距离dm,n与任务卸载模型，获取低轨卫星与无人船之间的距离dm,n的通信模型，其表达式为

35、

36、式中：rm表示无人船m与低轨卫星n之间的通信传输速率；w表示通信带宽；pm表示无人船m的发送功率；hm,n表示信道增益；n0表示高斯白噪声；表示无人船m与低轨卫星n之间任务卸载的传输时间；表示无人船m与低轨卫星n之间任务卸载的传输能耗。

37、进一步的，s2中获取的任务卸载的时间/能耗计算模型包括水下机器人的时间/能耗计算模型、无人船的时间/能耗计算模型以及低轨卫星的时间/能耗计算模型；

38、所述水下机器人的时间/能耗计算模型具体为

39、假设ρi表示水下机器人i总的cpu计算量，εi表示水下机器人i的能耗参数；则完成网络任务λi中部分任务所花费的计算时间表示为且其对应的计算花费的能耗表示为

40、所述无人船的时间/能耗计算模型具体为

41、假设ρm表示无人船m总的cpu计算量，εm表示无人船m的能耗参数，则完成任务λi中部分任务所花费的计算时间表示为且其对应的计算花费的能耗表示为

42、所述低轨卫星的时间/能耗计算模型具体为

43、假设ρn表示低轨卫星n总的cpu计算量，εn表示卫星n的能耗参数，则完成任务λi中部分任务所花费的计算时间表示为且其对应的计算花费的能耗表示为

44、进一步的，所述s3具体包括以下步骤：

45、s31：计算并获取水下机器人i独立完成计算任务所花费的时间为

46、s32：计算并获取水下机器人通过任务卸载后完成计算任务所花费的时间为

47、s33：根据步骤s31与s32，获取水下机器人完成任务所节省的时间为以构建水下机器人i的任务效率满意度函数模型为

48、其中ξi表示调整参数。

49、进一步的，所述s4具体包括以下步骤

50、s41：定义水下机器人i卸载至无人船m的网络任务为则需要支付给无人船m的任务卸载费用为其中ki表示支付给无人船的单位比特数据的价格；

51、且水下机器人i的自身能耗代价为其中qi表示水下机器人i自身单位能耗的价格；

52、s42：基于所述水下机器人的任务效率满意度函数模型，根据水下机器人的任务卸载费用与其自身能耗代价构建水下机器人效用函数zi，其表达式为

53、

54、进一步的，所述s5具体包括以下步骤：

55、s51：定义无人船m的自身能耗代价为其中qm表示无人船m自身单位能耗的价格；

56、并根据水下机器人的任务卸载费用构建无人船的效用函数zm，其表达式为

57、

58、式中：表示无人船需要支付给卫星的费用；

59、s52：定义低轨卫星n的自身能耗代价为其中qn表示低轨卫星n自身单位能耗的价格；

60、并根据无人船要支付给卫星的费用构建低轨卫星的效用函数，其表达式为

61、

62、进一步的，s6中获取的优化目标模型，其表达式为

63、p1:

64、p2:

65、p3:

66、其中公式p1与公式p2即为水下机器人与无人船之间的第一效用函数优化模型；公式p2与公式p3即为无人船与低轨卫星之间的第二效用函数优化模型。

67、进一步的，所述s7具体包括以下步骤：

68、s71：对第一效用函数优化模型进行求解，将第一效用函数优化模型的效用函数优化问题建模为斯塔克尔伯格博弈模型，以用于使水下机器人根据无人船给定的价格确定其网络任务卸载的比例，使无人船通过调整价格以达到水下机器人与无人船的斯塔克尔伯格博弈均衡，进而确定出卸载比例ai,m的最优解，具体包括以下三种求解情况；

69、s711：当时，通过求解水下机器人的效用函数对卸载比例的一阶导数与二阶导数，即

70、

71、由于其二阶导数是小于0的，则令能够得到卸载比例ai,m的最优解为

72、s712：当时，通过求解水下机器人的效用函数对卸载比例的一阶导数与二阶导数确定其凹性，即

73、

74、其中且其二阶导数是小于0的；

75、则令能够得到卸载比例ai,m的最优解为

76、

77、s713：当时，通过求水下机器人的效用函数对卸载比例的一阶导数与二阶导数，即

78、

79、

80、其中

81、由于其二阶导数是小于0的；则令可得卸载比例ai,m的最优解

82、为

83、

84、s72：根据确定的卸载比例ai,m的最优解，以确定水下机器人与无人船效用函数的最大值；

85、s73：对第二效用函数优化模型进行求解，将第二效用函数优化模型的效用函数优化问题建模为讨价还价博弈模型，以用于使得无人船和低轨卫星针对二者的各自出价的差值利润进行分配，求解最优的分配比例以达到二者的讨价还价博弈均衡，进而获取无人船和低轨卫星之间的交易价格具体包括以下步骤

86、s731：建立无人船的折扣因子模型μm与低轨卫星的折扣因子模型μn为

87、

88、式中：γm与γn分别表示为折扣因子的调整参数；

89、s732：基于鲁宾斯坦的讨价还价模型，根据无人船的折扣因子模型μm与低轨卫星的折扣因子模型μn，求解利润分配因子

90、s733：建立无人船的满意度函数模型um与低轨卫星的满意度函数模型un为

91、s734：基于步骤s51、步骤s52以及步骤s733，确定无人船的出价φm(bm,n)与低轨卫星的出价φn(bm,n)分别为

92、

93、s735：根据步骤s732与步骤s734，确定无人船与低轨卫星的交易价格其表达式为

94、

95、有益效果：本发明一种基于博弈论的海上边缘计算网络任务卸载方法，根据构建的水下机器人效用函数、无人船的效用函数以及低轨卫星的效用函数进行优化问题建模，获取包括下机器人与无人船之间的第一效用函数优化模型、无人船与低轨卫星之间的第二效用函数优化模型；并通过斯塔克尔伯格博弈模型对第一效用函数优化模型进行求解，通过讨价还价博弈模型对第二效用函数优化模型进行求解，获取第一效用函数优化模型与第二效用函数优化模型最大值对应的任务卸载及价格方案。该方法能有效均衡用户及系统的利益，能集中式完成调度，相比于传统的调度方式，更符合实际任务卸载状态，避免资源浪费，为在移动边缘计算系统中实施多任务卸载提供保证。