基于量子线路的模拟方法、装置、设备及可读存储介质与流程

本技术涉及量子计算，特别是涉及一种基于量子线路的模拟方法、装置、设备及可读存储介质。

背景技术：

1、随机计算机技术的不断发展，可以利用其计算优势对不同的系统进行模拟仿真，并构建该系统的线性方程组，通过对该线性方程组进行求解，可以得到该系统在稳定状态下的信息。如，在cfd(computational fluid dynamics，计算流体动力学)中，可以基于各种离散化的数学方法，对流体力学的问题进行数值实验、计算机模拟和分析研究。例如，利用cfd可以计算流体在稳定状态下不同位置处的温度、密度等状态信息。

2、现有技术中，在通过计算流体动力学模拟流体运动的过程中，需要求解线性方程组ax＝b，即求得x；x表示流体的状态，a表示系数矩阵。在计算过程中必须对a求逆，且该系数矩阵的维数与针对流体构建的网格节点成线性关系，当网格节点规模很大时，对该系数矩阵求逆的计算非常复杂，也就会增大计算的复杂度，导致确定状态的效率不高。

技术实现思路

1、本技术实施例的目的在于提供一种基于量子线路的模拟方法、装置、设备及可读存储介质，能够降低计算的复杂度，提高确定物理量的效率。具体技术方案如下：

2、本技术实施例的第一方面，首先提供了一种基于量子线路的模拟方法，所述方法包括：

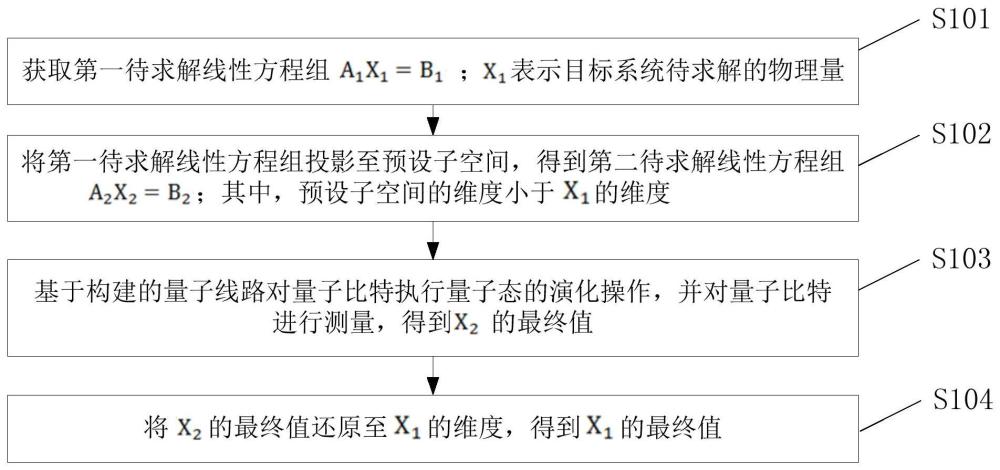
3、获取第一待求解线性方程组a1x1＝b1；x1表示目标系统待求解的物理量；

4、将所述第一待求解线性方程组投影至预设子空间，得到第二待求解线性方程组a2x2＝b2；其中，所述预设子空间的维度小于x1的维度；

5、基于构建的量子线路对量子比特执行量子态的演化操作，并对所述量子比特进行测量，得到x2的最终值；其中，所述量子线路是基于a2的逆矩阵对应的切比雪夫多项式构建的；所述量子线路的输入包含b2对应的量子比特的初态；

6、将x2的最终值还原至x1的维度，得到x1的最终值。

7、可选的，所述目标系统表示流体，x1表示针对所述流体的离散化网络中各网格单元在一个时刻与前一个时刻的待求解流体状态的差值；b1表示与前一个时刻的待求解流体状态和所述网格单元的坐标信息相关的残差量；a1表示与前一个时刻的待求解流体状态和所述网格单元的坐标信息相关的系数矩阵。

8、可选的，在所述基于构建的量子线路对量子比特执行量子态的演化操作，并对所述量子比特进行测量，得到x2的最终值之前，所述方法还包括：

9、基于第一算式，构建a2的逆矩阵对应的切比雪夫多项式的每一阶；

10、所述第一算式为：

11、

12、其中，

13、

14、a2-1表示a2的逆矩阵；表示a2的逆矩阵对应的切比雪夫多项式的第g阶；b＝κ2log(κ/∈)，κ表示条件数；∈表示预设精度值；c表示求组合数。

15、可选的，所述量子线路包括第一oracle和第二oracle；

16、所述第一oracle，用于实现基于量子行走算法，将a2的逆矩阵对应的切比雪夫多项式的每一阶编码至b2对应的量子比特的初态的振幅；

17、所述第二oracle，用于实现基于算符线性组合算法和所述第一oracle的编码结果，将a2的逆矩阵对应的切比雪夫多项式的各阶的加权和编码至b2对应的量子比特的初态的振幅。

18、可选的，所述量子线路的输入还包括第一数目个第一辅助量子比特，以及第二数目个第二辅助量子比特；

19、所述第一oracle，用于实现基于第二算式，将a2的逆矩阵对应的切比雪夫多项式的每一阶编码至b2对应的量子比特的初态的振幅；

20、所述第二算式为：

21、其中，算符用于实现从|0m>|b2>到的映射；π|φ⊥>＝0，

22、d表示a2的稀疏度；表示a2中第j行第k列的元素，且满足n表示a2的维度；算符用于实现从|0m>|ψj>到t|ψj>的映射；表示计算张量积；i表示单位矩阵；|0m>表示所述第二数目个第二辅助量子比特；|b2>表示b2对应的量子比特的初态；表示厄米共轭算符；wg表示所述切比雪夫多项式的第g阶对应的w算符；

23、所述第二oracle，用于实现基于第三算式，将a2的逆矩阵对应的切比雪夫多项式的各阶的加权和编码至b2对应的量子比特的初态的振幅；

24、所述第三算式为：

25、其中，g算符用于实现从|0r>|0m>|b2>到的映射，|ψ⊥>与t|j>正交；|0r>表示所述第一数目个第一辅助量子比特；α＝∑gαg。

26、可选的，所述第一数目为基于第四算式确定的，所述第四算式为：

27、r＝logm

28、其中，r表示所述第一数目，m表示a2的逆矩阵对应的切比雪夫多项式的阶数；

29、所述第二数目为基于第五算式确定的，所述第五算式为：

30、m＝log4n

31、m表示所述第二数目。

32、可选的，所述对所述量子比特进行测量，得到x2的最终值，包括：

33、对所述量子比特进行测量，得到所述第一辅助量子比特和所述第二辅助量子比特对应的寄存器均为|0>态时，b2对应的量子比特对应的寄存器的测量结果；

34、基于得到的测量结果，得到x2的最终值。

35、可选的，所述基于得到的测量结果，得到x2的最终值，包括：

36、基于得到的测量结果，得到x2当前的备选值；

37、基于x2当前的备选值，计算所述第二待求解线性方程组对应的残量；

38、若计算得到的残量满足第一终止条件，则基于x2当前的备选值确定x2的最终值；

39、若计算得到的残量不满足第一终止条件，则基于计算得到的残量进行迭代运算，并基于迭代运算的结果确定x2的最终值。

40、可选的，所述将x2的最终值还原至x1的维度，得到x1的最终值，包括：

41、按照第六算式，将x2的最终值还原至x1的维度，得到x1的最终值；所述第六算式为：

42、x1＝x0+vdx2

43、其中，x0表示进行投影时的初始解；vd表示进行投影时确定出的所述预设子空间的一组基。

44、本技术实施例的第二方面，提供了一种基于量子线路的模拟装置，所述装置包括：

45、获取模块，用于获取第一待求解线性方程组a1x1＝b1；x1表示目标系统待求解的物理量；

46、投影模块，用于将所述第一待求解线性方程组投影至预设子空间，得到第二待求解线性方程组a2x2＝b2；其中，所述预设子空间的维度小于x1的维度；

47、演化模块，用于基于构建的量子线路对量子比特执行量子态的演化操作，并对所述量子比特进行测量，得到x2的最终值；其中，所述量子线路是基于a2的逆矩阵对应的切比雪夫多项式构建的；所述量子线路的输入包含b2对应的量子比特的初态；

48、还原模块，用于将x2的最终值还原至x1的维度，得到x1的最终值。

49、可选的，所述目标系统表示流体，x1表示针对所述流体的离散化网络中各网格单元在一个时刻与前一个时刻的待求解流体状态的差值；b1表示与前一个时刻的待求解流体状态和所述网格单元的坐标信息相关的残差量；a1表示与前一个时刻的待求解流体状态和所述网格单元的坐标信息相关的系数矩阵。

50、可选的，所述装置还包括：

51、构建模块，用于在所述基于构建的量子线路对量子比特执行量子态的演化操作，并对所述量子比特进行测量，得到x2的最终值之前，基于第一算式，构建a2的逆矩阵对应的切比雪夫多项式的每一阶；

52、所述第一算式为：

53、

54、其中，

55、

56、a2-1表示a2的逆矩阵；表示a2的逆矩阵对应的切比雪夫多项式的第g阶；b＝κ2log(κ/∈)，κ表示条件数；∈表示预设精度值；c表示求组合数。

57、可选的，所述量子线路包括第一oracle和第二oracle；

58、所述第一oracle，用于实现基于量子行走算法，将a2的逆矩阵对应的切比雪夫多项式的每一阶编码至b2对应的量子比特的初态的振幅；

59、所述第二oracle，用于实现基于算符线性组合算法和所述第一oracle的编码结果，将a2的逆矩阵对应的切比雪夫多项式的各阶的加权和编码至b2对应的量子比特的初态的振幅。

60、可选的，所述量子线路的输入还包括第一数目个第一辅助量子比特，以及第二数目个第二辅助量子比特；

61、所述第一oracle，用于实现基于第二算式，将a2的逆矩阵对应的切比雪夫多项式的每一阶编码至b2对应的量子比特的初态的振幅；

62、所述第二算式为：

63、其中，算符用于实现从|0m>|b2>到的映射；π|φ⊥>＝0，d表示a2的稀疏度；表示a2中第j行第k列的元素，且满足n表示a2的维度；算符用于实现从|0m>|ψj>到t|ψj>的映射；表示计算张量积；i表示单位矩阵；|0m>表示所述第二数目个第二辅助量子比特；|b2>表示b2对应的量子比特的初态；表示厄米共轭算符；wg表示所述切比雪夫多项式的第g阶对应的w算符；

64、所述第二oracle，用于实现基于第三算式，将a2的逆矩阵对应的切比雪夫多项式的各阶的加权和编码至b2对应的量子比特的初态的振幅；

65、所述第三算式为：

66、其中，g算符用于实现从|0r>|0m>|b2>到的映射，|ψ⊥>与t|j>正交；|0r>表示所述第一数目个第一辅助量子比特；α＝∑gαg。

67、可选的，所述第一数目为基于第四算式确定的，所述第四算式为：

68、r＝logm

69、其中，r表示所述第一数目，m表示a2的逆矩阵对应的切比雪夫多项式的阶数；

70、所述第二数目为基于第五算式确定的，所述第五算式为：

71、m＝log4n

72、m表示所述第二数目。

73、可选的，所述演化模块，包括：

74、测量子模块，用于对所述量子比特进行测量，得到所述第一辅助量子比特和所述第二辅助量子比特对应的寄存器均为|0>态时，b2对应的量子比特对应的寄存器的测量结果；

75、生成子模块，用于基于得到的测量结果，得到x2的最终值。

76、可选的，所述生成子模块，具体用于基于得到的测量结果，得到x2当前的备选值；

77、基于x2当前的备选值，计算所述第二待求解线性方程组对应的残量；

78、若计算得到的残量满足第一终止条件，则基于x2当前的备选值确定x2的最终值；

79、若计算得到的残量不满足第一终止条件，则基于计算得到的残量进行迭代运算，并基于迭代运算的结果确定x2的最终值。

80、可选的，所述还原模块，具体用于按照第六算式，将x2的最终值还原至x1的维度，得到x1的最终值；所述第六算式为：

81、x1＝x0+vdx2

82、其中，x0表示进行投影时的初始解；vd表示进行投影时确定出的所述预设子空间的一组基。

83、本技术实施例的第三方面，提供了一种量子计算机设备，包括：量子线路及寄存器，所述量子计算机设备在运行时实现上述任一所述的方法。

84、本技术实施例的第四方面，提供了一种计算机可读存储介质，所述计算机可读存储介质内存储有计算机程序，所述计算机程序被处理器执行时实现上述任一所述的方法步骤。

85、本技术实施例有益效果：

86、本技术实施例提供的基于量子线路的模拟方法，获取第一待求解线性方程组a1x1＝b1；x1表示目标系统待求解的物理量；将第一待求解线性方程组投影至预设子空间，得到第二待求解线性方程组a2x2＝b2；其中，预设子空间的维度小于x1的维度；基于构建的量子线路对量子比特执行量子态的演化操作，并对量子比特进行测量，得到x2的最终值；其中，量子线路是基于a2的逆矩阵对应的切比雪夫多项式构建的；量子线路的输入包含b2对应的量子比特的初态；将x2的最终值还原至x1的维度，得到x1的最终值。

87、基于上述处理，由于x2可以基于a2的逆矩阵和b2得到，而量子线路是基于a2的逆矩阵对应的切比雪夫多项式构建的，且量子线路的输入包含b2对应的量子比特的初态，因此，在演化后，基于对量子比特的测量结果，也就能够得到x2的值。相应的，还可以将x2的最终值还原至x1的维度，也就可以得到x1的值。由于预设子空间的维度小于x1的维度，因此，基于量子线路对第二待求解线性方程组进行求解，能够降低计算的复杂度，也就能够提高确定状态的效率。

88、当然，实施本技术的任一产品或方法并不一定需要同时达到以上所述的所有优点。