基于精确模型的二阶相关近场源三维参数欠定估计方法

本发明涉及近场源定位，尤其是涉及一种基于精确模型的二阶相关近场源三维参数欠定估计方法。

背景技术：

1、近场源定位在通信、雷达、声纳等众多领域中已广泛应用。许多定位算法是为远场源而开发的，近场源的相位差为非线性，相较于远场源的定位实现更加困难。为了应用远场源的定位算法实现近场源的定位，很多研究忽略了相对于参考阵元的幅度衰减，并对相位差进行了菲涅尔近似处理，但是定位算法的参数估计精度受到了限制。大多数定位算法均是基于均匀阵列提出的，相较于均匀阵列，采用非均匀阵列能够减少传感器的数量和增加阵列孔径，并且通过数据处理能够获得更高的自由度，为实现近场源的欠定估计提供了条件，即信源数大于阵元数的情况。此外，利用接收数据的时间信息能够提高定位算法的估计性能。在实际应用中，三维场景更符合实际情况，许多三维参数估计算法具有较高的计算量，且能够实现欠定估计的算法较少。在近场源定位中，还尚未提出过基于精确模型的二阶相关近场源三维参数欠定估计方法。

技术实现思路

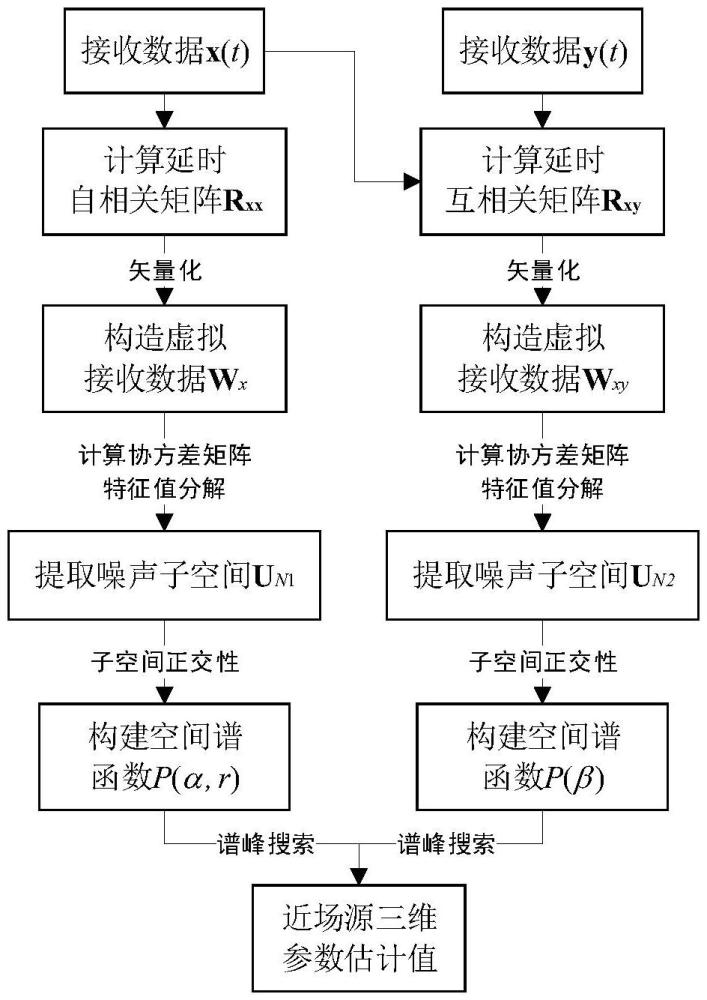
1、本发明所要解决的技术问题是提供一种基于精确模型的二阶相关近场源三维参数欠定估计方法，其基于近场源三维空间精确传播模型，联合空时信息计算接收数据的自相关和互相关矩阵，利用信号子空间和噪声子空间的正交性，通过一次二维谱峰搜索和一次一维搜索实现欠定估计近场源角度和距离参数，无需参数匹配且复杂度低。

2、本发明解决上述技术问题所采用的技术方案为：一种基于精确模型的二阶相关近场源三维参数欠定估计方法，其特征在于包括以下步骤：

3、步骤1：建立基于l型嵌套阵列的近场源三维空间精确传播模型，所述模型包括k个窄带近场源、l型嵌套阵列，以及基于窄带近场源和l型嵌套阵列建立的数学模型，l型嵌套阵列由位于三维空间的x轴上和y轴上的两个嵌套阵列构成，对应定义为阵列x和阵列y；

4、第k个窄带近场源的三维参数记为(αk,βk,rk)，其中，k＝1,2,…,k，k≥1，αk表示第k个窄带近场源的入射方向与x轴的夹角，αk∈[0,π]，βk表示第k个窄带近场源的入射方向与y轴的夹角，βk∈[0,π]，rk表示第k个窄带近场源与三维空间的原点的距离，rk∈(0,2d2/λ]，d表示l型嵌套阵列的孔径，λ为信号波长；

5、阵列x的总阵元个数为n，阵列x为由两个均匀线阵先后嵌套在一起组成的线阵，组成阵列x的第1个均匀线阵的阵元个数和相邻阵元间距对应为lx和d、第2个均匀线阵的阵元个数和相邻阵元间距对应为n-lx和(lx+1)d，组成阵列x的第1个均匀线阵的第1个阵元和第2个均匀线阵的最后一个阵元对应作为阵列x的第1个阵元和最后一个阵元，组成阵列x的第1个均匀线阵的最后一个阵元与第2个均匀线阵的第1个阵元之间存在线阵间距，阵列x的第n个阵元在三维空间的横坐标为当n∈[1,lx]时当n∈[lx+1,n]时阵列x的第n个阵元与第k个窄带近场源的距离为其中，lx＞1，n-lx＞1，n＝1,2,…,n；

6、阵列y的总阵元个数为m，阵列y也为由两个均匀线阵先后嵌套在一起组成的线阵，组成阵列y的第1个均匀线阵的阵元个数和相邻阵元间距对应为ly和d、第2个均匀线阵的阵元个数和相邻阵元间距对应为m-ly和(ly+1)d，组成阵列y的第1个均匀线阵的第1个阵元和第2个均匀线阵的最后一个阵元对应作为阵列y的第1个阵元和最后一个阵元，组成阵列y的第1个均匀线阵的最后一个阵元与第2个均匀线阵的第1个阵元之间存在线阵间距，阵列y的第m个阵元在三维空间的纵坐标为当m∈[1,ly]时当m∈[ly+1,m]时阵列y的第m个阵元与第k个窄带近场源的距离为其中，ly＞1，m-ly＞1，m＝1,2,…,m；

7、k个窄带近场源入射到l型嵌套阵列中，将基于窄带近场源和l型嵌套阵列的数学模型表示为：其中，t表示时间变量，x(t)表示阵列x的接收数据矢量，α表示窄带近场源的入射方向与x轴的夹角，r表示窄带近场源与三维空间的原点的距离，α和r为变量，ax(α,r)表示阵列x的流形矩阵，ax(α,r)的维度为n×k，ax(α,r)＝[ax(α1,r1),ax(α2,r2),…,ax(αk,rk)]，ax(αk,rk)为导向矢量，ax(αk,rk)的维度为n×1，表示阵列x的第n个阵元对第k个窄带近场源的空间幅度相位因子，g表示已知的路径损耗衰减指数，e为自然常数，j为虚数单位，λ为信号波长，上标“t”表示矩阵或向量的转置，s(t)表示信号矢量，s(t)的维度为k×1，s(t)＝[s1(t),s2(t),…,sk(t)]t，sk(t)表示第k个窄带近场源入射的信号，nx(t)表示x(t)中的高斯白噪声矢量，nx(t)的维度为n×1，y(t)表示阵列y的接收数据矢量，β表示窄带近场源的入射方向与y轴的夹角，β为变量，ay(β,r)表示阵列y的流形矩阵，ay(β,r)的维度为m×k，ay(β,r)＝[ay(β1,r1),ay(β2,r2),…,ay(βk,rk)]，ay(βk,rk)为导向矢量，ay(βk,rk)的维度为m×1，表示阵列y的第m个阵元对第k个窄带近场源的空间幅度相位因子，ny(t)表示y(t)中的高斯白噪声矢量，ny(t)的维度为m×1；

8、步骤2：在步骤1的基础上，计算阵列x的接收数据矢量x(t)的延时自相关矩阵rxx(τ)，然后对rxx(τ)进行矢量化计算，得到rxx(τ)的矢量化结果rxx(τ)，

9、rxx(τ)＝vec{rxx(τ)}

10、

11、再取τ＝ts,2ts,…,npts，得到由阵列x的接收数据矢量x(t)构造出的虚拟接收数据矩阵wx，wx＝[rxx(ts),rxx(2ts),…,rxx(npts)]＝bxρs；其中，τ表示延时变量，e{·}表示数学期望，(·)h为共轭转置运算，x(t+τ)表示x(t)延时τ后的结果，ax即为ax(α,r)，rs(τ)表示信号矢量s(t)的协方差矩阵，rs(τ)＝e{s(t)sh(t+τ)}，s(t+τ)表示s(t)延时τ后的结果，δ(·)为狄利克雷函数，rn(τ)表示x(t)中的高斯白噪声矢量nx(t)的协方差矩阵，nx(t+τ)表示nx(t)延时τ后的结果，在高斯白噪声假设下当τ＝0时表示噪声功率，in表示n阶单位阵，当τ≠0时rn(τ)中的所有元素均为0，vec{·}表示矢量化，⊙为khatri-rao积运算，上标“*”表示复共轭，ρs(τ)＝diag{rs(τ)}，diag{·}表示取主对角线元素，bx表示阵列x的虚拟流形矩阵，bx的第k列向量为bx(αk,rk)，bx(αk,rk)为导向矢量，为kronecker积运算，ts表示虚拟采样间隔，np表示伪快拍数，ρs表示虚拟信号矩阵，ρs＝[ρs(ts),ρs(2ts),…,ρs(npts)]；

12、步骤3：在步骤2的基础上，计算wx的协方差矩阵然后对进行特征值分解，并取最小的n2-k个特征值对应的特征向量构成噪声子空间导向矢量bx(α,r)属于信号子空间，利用信号子空间与噪声子空间的正交性，并根据α的范围α∈[0,π]和r的范围r∈(0,2d2/λ]，计算关于α和r的空间谱函数p(α,r)，再通过对p(α,r)进行二维谱峰搜索，得到k个峰值，第k个峰值所在位置对应的两个参数即为αk和rk各自的估计值，对应为和其中，表示ρs的协方差矩阵，ax(α,r)为ax(αk,rk)中的参数替换成变量后的形式；

13、步骤4：在步骤1的基础上，计算阵列x的接收数据矢量x(t)与阵列y的接收数据矢量y(t)的延时互相关矩阵rxy(τ)，然后对rxy(τ)进行矢量化计算，得到rxy(τ)的矢量化结果rxy(τ)，再取τ＝ts,2ts,…,npts，得到由阵列x的接收数据矢量x(t)和阵列y的接收数据矢量y(t)构造出的虚拟接收数据矩阵wxy，wxy＝[rxy(ts),rxy(2ts),…,rxy(npts)]＝bρs；其中，y(t+τ)表示y(t)延时τ后的结果，ay即为ay(β,r)，b表示阵列x和阵列y的虚拟流形矩阵，b的第k列向量为b(αk,βk,rk)，

14、步骤5：在步骤4的基础上，计算wxy的协方差矩阵然后对进行特征值分解，并取最小的n×m-k个特征值对应的特征向量构成噪声子空间导向矢量b(α,β,r)属于信号子空间，利用信号子空间和噪声子空间的正交性，并根据β的范围β∈[0,π]，同时将和代入关于β的空间谱函数中，再通过对p(β)进行一维谱峰搜索，得到一个峰值，这个峰值所在位置对应的参数即为βk的估计值其中，ay(β,r)为ay(βk,rk)中的参数替换成变量后的形式，ax(α,r)为ax(αk,rk)中的参数替换成变量后的形式，为将和代入b(α,β,r)后的形式。

15、所述步骤1中，d＝λ/2，λ为信号波长。

16、所述步骤1中，线阵间距的值为d。

17、与现有技术相比，本发明的优点在于：

18、采用l型嵌套阵列，联合接收数据的空时信息，计算自相关和互相关矩阵，构造虚拟接收数据矩阵，根据信号子空间与噪声子空间的正交性得到空间谱函数，通过一次二维谱峰搜索和一次一维谱峰搜索实现近场源角度和距离参数的估计。同时，在参数估计过程中，利用信号空时特性构造虚拟接收数据矩阵，提高了l型嵌套阵列的自由度，可实现近场源的欠定估计。本发明方法与已有的算法相比，能够有效降低复杂度并估计更多数量的近场源，无需参数匹配过程且具有更高的参数估计精度。