基于自适应神经模糊推理燃料电池船舶能量管理策略的方法

本发明涉及船舶能量管理策略，特别是面向燃料电池船舶高波动负载的功率适配性，以及全航程下的燃油经济性要求的应用方法。

背景技术：

1、在车载燃料电池动力系统领域中，由于单一燃料电池动态响应缓慢，无法快速跟踪负载变化以满足日常驾驶需求，必须配备蓄电池作为缓冲单元或者增程器，从而要求其能量管理策略以功率适配性、燃油经济性和续航能力为控制目标。尤其面对车辆频繁启停和负载变化的特征，其能量管理策略优先保障续航能力。而对于船舶燃料电池电力推进系统而言，船舶续航能力同样受限于储氢量。但相比于车辆，船舶的载重与空间充足，对于储氢系统的要求并不像车辆那样严苛。因此，在船舶的续航能力有一定的保障前提下，其面临的主要问题为船舶的大功率设备较多，且由于航行过程中受到航线环境与航道的影响，工况变化复杂，尤其是船舶的启停过程负载发生较高频率的波动，这加剧了能量管理系统设计的难度。那么，船舶燃料电池能量管理策略更加侧重于面向高波动负载时的功率适配性和全航程的燃油经济性。

2、船舶燃料电池能量管理策略常见的方法有基于规则的策略、基于全局优化和基于瞬时优化的策略。其中，基于规则的能量管理策略过于依赖经验值，只可满足功率的适配性，很难实现对燃料经济性的精准控制。动态规划法(dp)是基于全局优化的一种离线算法，可实现全局最优，但其面对多维变量和复杂方程过于依赖能量管理系统的算力，且耗时长，难以用于实时控制。等效氢消耗最小算法(ecms)是基于瞬时优化算法的一种在线算法，其控制性能依赖于等效因子的选取，且优化效果与dp算法的全局最优解相比较差，仍有提升空间。那么，针对燃料电池船舶面向高波动负载的功率适配性，以及全航程下的燃油经济性要求，基于瞬时优化算法的ecms能量管理策略如何学习借鉴基于dp算法确定的全局最优解，从而实现快速可靠的在线控制。因此，需要提出一种燃料电池船舶能量管理策略的新方法。

技术实现思路

1、有鉴于此，上述基于规则、全局优化和瞬时优化策略建立的方法仍未能有效地解决船舶高波动负载的多电源能量管理策略问题。本发明的目的在于提供一种基于自适应神经模糊推理燃料电池船舶能量管理策略的方法，面对船舶航行的高波动负载工况下功率适配性，以及全航程下的燃油经济性要求，不仅参考了动态规划(dp)算法的全局最优结果，同时经过训练的自适应神经模糊推理系统(anfis)网络具有了在线计算的能力，用于改进传统ecms的等效因子计算以提高效率。

2、为实现上述目的，本发明采用如下技术方案：运用anfis计算ecms等效因子以实现在线理想功率分配的改进法，包括以下步骤：

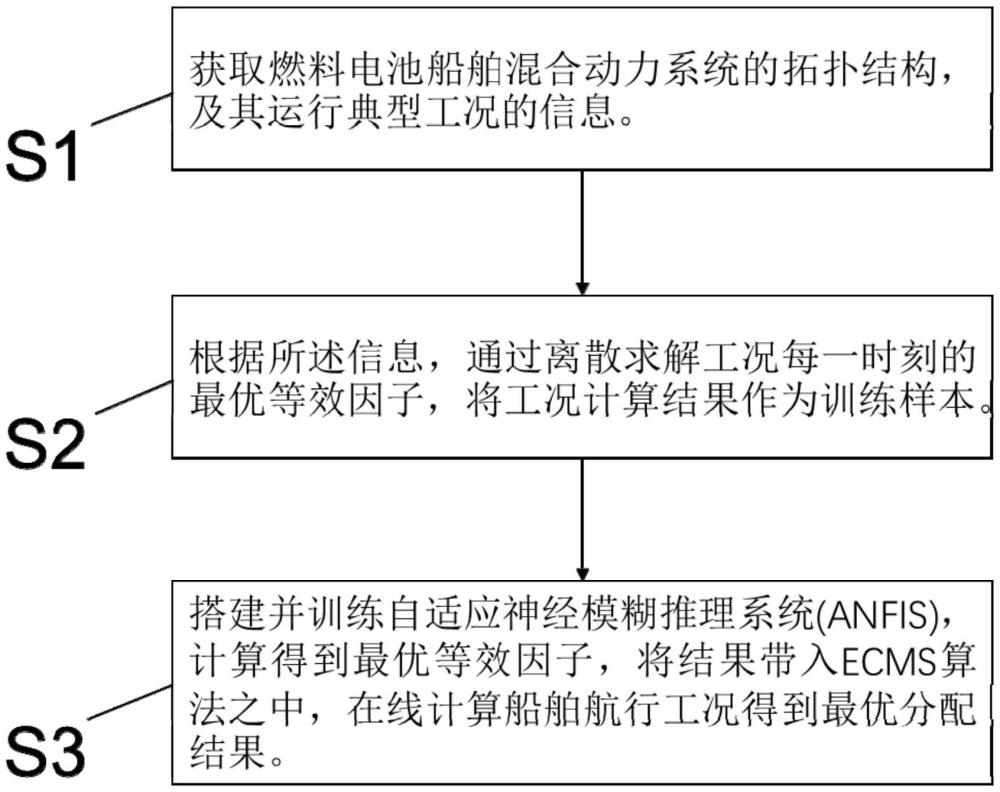
3、步骤s1：获取燃料电池船舶混合动力系统的拓扑结构，及其运行典型工况的信息；

4、步骤s2：根据所述信息，通过离散求解工况每一时刻的最优等效因子，将工况计算结果作为训练样本；

5、步骤s3:搭建并训练anfis，计算得到最优等效因子，将结果带入ecms算法之中，在线计算船舶航行工况得到最优分配结果。

6、所述步骤s1包括以下步骤：

7、步骤s1：获取燃料电池船舶混合动力系统的拓扑结构，及其运行典型工况的信息；

8、步骤s11:以质子交换膜燃料电池、蓄电池、超级电容以及推进系统构成的燃料电池船舶；

9、所述海上船舶的固定工况和行驶状态具体包括船舶的工况信息、船舶的航行参数、船舶的负载功率需求。

10、针对燃料电池船舶面向高波动负载的功率适配性，以及全航程下的燃油经济性要求，根据具体的功率变化幅度和范围，船舶负载工况可分为两种：定速巡航和增程模式。其中定速巡航定义为船舶负载工况变化稳定，以燃料电池作为主动力的航行工况。增程模式定义为船舶启动或者靠港等运行状况下，船舶所需负载工况变化波动大且不稳定，燃料电池以增程模式运行的工况。

11、建立船舶混合燃料电池动力系统，船舶混合燃料电池动力系统可由燃料电池能量系统、锂电池能量系统及超级电容能量系统组成，并根据所述的混合燃料电池系统，建立出对应的数学模型。

12、在满足负载功率的前提下，为了更好地提高电池的使用寿命，采用一种小波变化的功率分配方法。通过三层的haar小波变换对负载功率进行分解重构，将重构的高频功率作为超级电容输出结果，低频功率作为燃料电池和锂电池的输出。haar小波变换的函数式为：

13、

14、以燃料电池复合能量源的系统等效耗氢作为dp算法的目标函数，其中系统等效耗氢由燃料电池的直接耗氢与锂电池的等效耗氢两部分组成每阶段的实时等效氢消耗表达式如下：

15、g(t)＝cfc(t)+βcbat(t)

16、其中g(t)为t阶段的等效氢消耗量。cfc和cbat为燃料电池和锂电池的等效耗氢；

17、为了确保锂电池的soc、燃料电池和锂电池的输出功率都保持在合理的界限内，提出边界约束条件如下：

18、

19、式中：pbat,min和pbat,max为锂电池输出功率的最小最大值；pfc,min和pfc,max为燃料电池输出功率的最小最大值。锂电池的soc最大值为70％，最小值为50％。

20、dp算法在求解多阶段的决策问题时，通过基本递推公式逆向递推，基于t+1阶段的状态可通过状态转移方程求解得到t阶段的状态值，控制锂电池初始和末尾的soc为60％，状态转移方程如下：

21、soc(t+1)＝f(soc(t),pfc(t),pbat(t))

22、综上所述，dp算法的累计目标函数为：

23、j(t)＝j(t-1)+g(t)

24、ecms策略作为瞬时优化策略，它由pmp策略推演而来，通过求解哈密尔顿函数极值问题将一个全局优化问题转化成每一步的瞬时优化问题。在数学上，混合动力系统的氢消耗控制问题可以概括为

25、

26、其中t0是初始时间，tf是最终时间。u(t)和x(t)分别是控制变量和状态变量。状态和控制变量由下式给出

27、

28、由于功率平衡，电池电量耗尽越多，所需的燃油消耗越少。因此，燃料消耗可以表示为电池功率的函数。在pmp的基础上，哈密顿函数h可由下式表示

29、h(x,u,λ,t)＝cfc+cbat+csc+λ1δsocbat

30、其中，cfc、cbat、csc分别为燃料电池、锂电池和超级电容的氢气消耗量，λ1和λ2为协态变量。由于锂电池的端电压和内阻不变，soc不随哈密顿函数变化，因此λ1为一个常数，即λ1＝c。

31、在此，等效因子可以定义为因此，ecms的目标函数可表示为

32、

33、以dp算法功率分配结果作为参考，通过离散寻优计算出ecms的最佳等效因子。在可给定等效因子的限定范围内，将等效因子s离散并在从大到小的搜索过程中逐一代入氢消耗最优控制公式，当控制变量差值最小时即为满足条件。

34、anfis是一种多层模型，能够将模糊定性方法与人工神经网络自适应能力相结合，以促进适应和学习，一般由几个模糊规则组成。搭建自适应神经模糊推理系统(anfis)，通用架构由五个具有神经结构的层组成，其不同层的描述如下所示

35、(1)

36、(2)

37、(3)

38、(4)

39、(5)

40、基于anfis的训练结果，在线计算最佳等效因子，并根据等效因子计算结果带入ecms算法进行功率分配计算。基于上述内容，本发明针对燃料电池船舶面向高波动负载的功率适配性，以及全航程下的燃油经济性要求，建立适配的燃料电池船舶混合动力系统，并结合了三种策略的计算特点，提出了基于动态规划的anfis优化ecms等效因子的改进法，能够在线计算得到船舶实时功率分配的最优解，具有较好的全局优化能力。

41、与现有技术相比，本发明具有以下有益效果：在建立anfis计算ecms等效因子以实现在线功率分配的过程中，通过船舶实际航行工况为参考建立混合燃料电池动力系统的数学模型，并以dp算法计算得到船舶氢消耗的最优控制分配路线。在此基础上，搭建了自适应神经模糊推理系统(anfis)，以全局最优计算结果为标准，对等效因子离散逐次计算得到最优值并作为训练数据，训练并实时应用于船舶工况的分析和能量管理。