基于GPU加速的全热平衡天然水温模拟方法

本发明属于河湖海域天然水温模拟，具体涉及基于gpu加速的全热平衡天然水温模拟方法。

背景技术：

1、水温作为地表水体重要的物理特征，直接影响着河湖海域生态系统中物理、化学和生物过程，成为决定水生态系统是否健康的关键参数之一。水温过高或过低都将不利于水生生物物种代谢、生长、发育和繁殖，甚至会导致水生态系统中生物群落以及种群结构发生剧烈变化。以往对天然水温的研究通常以描述性为基本态势，无法预测水温的发展趋势。同时，限于水温测量技术的发展水平，模型数据获取难度较大，造成水温模型精度不高。因此，构建高精度的天然水温模型对探究水温对水生态环境的影响显得尤为重要。当前，随着水温测量技术的不断发展，涌现出许多高精度的水温监测技术，为确定性水温模型准确模拟与预测复杂流态天然水温提供了可能。基于此，提出了一种基于gpu加速的全热平衡天然水温模拟方法。该方法采用全热平衡法原理，通过水体质量、热量平衡原理建立数值模型来模拟河湖海域内天然水温输移规律；同时引入gpu加速技术，以进一步提高模型模拟的高效性。该方法为准确、高效模拟河湖海域天然水温输移过程提供了重要的模拟工具，以便于更为准确地探究水温对水生态环境的影响。

技术实现思路

1、本发明的目的是提供基于gpu加速的全热平衡天然水温模拟方法，能够精确模拟河湖海域天然水温的动态输移过程。

2、本发明所采用的技术方案是，基于gpu加速的全热平衡天然水温模拟方法，具体按照以下步骤实施：

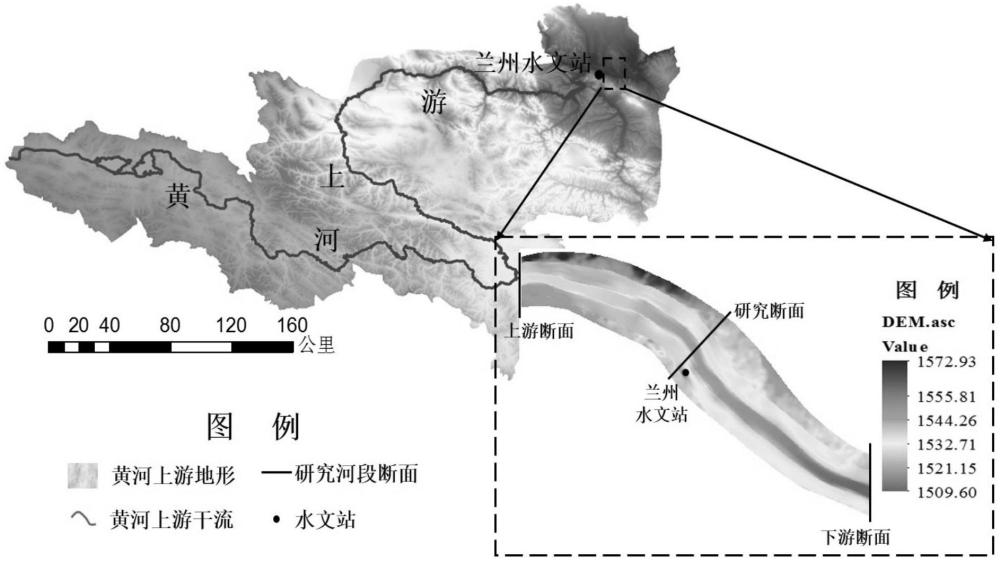
3、步骤1、通过高分辨率dem地形表征河湖海域的真实地形，以此作为模型输入的地形数据；

4、步骤2、对相关参数进行赋值；

5、步骤3、构建二维天然水温对流扩散输运方程；

6、步骤4、将水动力控制方程与构建二维天然水温对流扩散输运方程进行耦合，得到二维水动力-水温耦合控制方程组，离散上述二维水动力-水温耦合控制方程组，求解耦合控制方程组的通量项、扩散项和源项；

7、步骤5、满足河湖海域水体内收支平衡过程；

8、步骤6、有效处理干湿边界问题，实现模型的时空二阶精度；

9、步骤7、利用cfl条件对时间的稳定性加以限制；

10、步骤8、输出研究区域的天然水温输运过程。

11、本发明的特点还在于，

12、步骤3中二维天然水温对流扩散方程表示如下：

13、

14、式中，t为沿水深平均的水体增温量，单位为：℃；ex、ey分别为x、y方向上的热扩散系数；h为水深，单位为：m；u、v分别为x、y方向上的流速，单位为：m/s；t为时间，单位为：s；为净表面热通量，单位为：w/m2；ρ为水密度，单位为：kg/m3，cp为水体比热容通量，单位为：w/(m2·(kg·℃))，ti0为源汇项，单位为：℃。

15、步骤4中二维水动力-水温耦合控制方程的矢量形式表示如下：

16、

17、其中，

18、

19、式中，t为时间；q为变量矢量，其中，h为水深，单位为：m，qx和qy分别为x、y方向上的单宽流量，单位为：m2/s；f、g分别为x、y方向上的通量矢量；u、v分别为x、y方向上的流速，单位为：m/s；s为源项矢量，包括底坡源项及摩阻源项、温度扩散项和温度源项；zb为河床底面高程，单位为：m；cf为床面摩擦系数，计算式为cf＝gn2/h1/3，其中n为曼宁系数；g为重力加速度，单位为：m/s2；t为沿水深平均的水体增温量，单位为：℃；ex、ey分别为x、y方向上的热扩散系数；h为水深，单位为：m；为净表面热通量，单位为：w/m2；ρ为水密度，单位为：kg/m3，cp为水体比热容通量，单位为：w/(m2·(kg·℃))，ti0为源汇项，单位为：℃。

20、步骤4具体如下：

21、步骤4.1、第i个控制单元网格，采用中心有限体积法对水动力-水温控制方程组进行积分，转化为线积分，具体形式为：

22、

23、式中，ω为控制单元网格i的容积；γ为控制容积i的边界；n为控制容积边界γ所对应的外法线方向的单位向量；s为源项向量，包括底坡源项sb、摩阻源项sf、温度扩散项以及温度源项，k为控制单元网格边的编号；lk为第i个控制单元网格第k个边的边长；

24、对通量项采用hllc黎曼求解器进行求解，f(q)·n得到：

25、

26、其中，控制体单元网格界面中间通量f*为，

27、

28、控制体单元网格界面通量中间波两侧，f*l和f*r为，

29、

30、式中，fl和fr分别为单元网格界面左、右侧的通量；f*、和分别为控制体单元网格界面通量中间波两侧的左波通量、中间波通量和右波通量；u||为沿交界面的切向速度，u||＝-uny+vnx，u||l和u||r分别为控制体单元网格交界面的左侧、右侧切向速度，单位为m3/s；nx和ny分别为沿x和y的指示方向；u和v分别为沿x和y的单宽流量，单位为m/s；变量q⊥＝[h,qxnx+qyny]；qx和qy分别为沿x和y的单宽流量，单位为m2/s；sl、sm、sr分别为左波速、中间波速、右波速，单位为m/s；u⊥为通过网格单元界面垂直的速度，单位为m/s；u⊥＝unx+vny；h*和为中间变量；g为重力加速度，单位为m/s2；t为沿水深平均的水体增温量，单位为℃；

31、步骤4.2、扩散项作为源项，采用中心差分法进行求解，在网格单元界面上的值由两侧单元中心处的平均值来代替求解，式中的热扩散系数ex、ey由下式表示：

32、ex＝αu*h，ey＝βu*h                      (8)

33、式中，α、β为系数；h为水深，单位为m；u*为摩阻流速，单位为m/s；

34、步骤4.3、底坡源项采用底坡通量法求解，得到某一边f处的底坡通量的矢量形式为：

35、

36、式中，fsf(q)为某一边f处的底坡通量；nf为面f单位外法向量；nfx和nfy是nf与面f单位外法向量的组成部分，hl和zbl分别为网格单元中心处的水深和底部高程，与zml网格边上的水深和底部高程，g为重力加速度，单位为m/s2；

37、步骤4.4、摩阻源项采用显隐式摩阻处理法求解，计算公式为：

38、

39、其中，单宽流量更新为时间步长n+1时刻计算公式为，

40、

41、式中，sfx和sfy分别为sf在x和y方向的摩阻源项；cf为床面糙率系数，cf＝gn2/h1/3，n为曼宁系数，单位为s/m1/3；h为水深，单位为m；qx、qy分别为x、y方向上平均流速，单位为m2/s；qxn+1、qyn+1分别为时间步长n+1时刻在x、y方向上的单宽流量，单位为m2/s；qxn、qyn分别为时间步长n时刻在x、y方向上的单宽流量，单位为m2/s；δt为时间步长，单位为s；δqx为时间步长n时刻和n+1时刻的x方向上单宽流量之差，即δqx＝qxn+1-qxn，单位为m2/s。

42、步骤5具体如下：

43、步骤5.1、求解水气热交换的净热通量根据全热平衡温度法，将太阳短波净辐射通量、大气长波辐射通量和大气向水体的热传导通量作为水体表面热量的主要来源，将水体长波返回辐射通量、水体蒸发热通量以及水体向大气的热传导通量作为水体表面热量的损失源，由此得到，水气热交换的净热通量的求解公式如下：

44、

45、式中，为净表面热通量，单位为w/m2；为太阳短波净辐射引起的表面热通量，单位为w/m2；为太阳长波净辐射引起的表面热通量，单位为w/m2；为蒸发或凝结损失引起的表面通量，单位为w/m2；为水气热传导引起的表面热通量，单位为w/m2；

46、步骤5.2、求解公式(2)中逐项热通量项：太阳短波净辐射表面热通量，考虑水面反射率和云层覆盖率得：

47、

48、式中，为太阳短波净辐射表面热通量，单位为w/m2；rsrad为测量或计算得到的太阳短波辐射量，单位为w/m2；γ为水面反射率，c为云层覆盖率，β为水体表面吸收率；

49、太阳长波净辐射表面热通量，根据stenfan-boltzman辐射定律得到：

50、

51、式中，εa为空气长波发射率，σ为stenfan-boltzman常数，ta为气温，单位为℃；c为云层覆盖率，εw为水体的长波发射率，ts为水体表面水温，单位为℃；

52、蒸发或凝结表面通量，根据空气和水面的蒸发压力计算：

53、re＝f(wz)(es-ea)                      (16)

54、f(wz)＝9.2+0.46w2                      (17)

55、ea＝exp(2.3026×7.5td/(td+237.3)+0.6609)           (18)

56、es＝0.611×exp(17.3ts/(ts+237.3))              (19)

57、式中，re为蒸发或凝结表面通量，单位为w/m2；f(wz)在高度为zm处风速函数，单位为wm-2mmhg-1；es为水面的饱和蒸气压，单位为mmhg-1；ea为大气蒸气压，单位为mmhg-1；wz为水面以上2m的风速；

58、热传导表面热通量：

59、rc＝cf(wz)(ts-ta)                    (20)

60、式中：c为bowen’s系数，f(wz)在高度为z m处风速函数，单位为wm-2mmhg-1；ts为水体表面温度，单位为℃；ta为气温，单位为℃；

61、步骤5.3、根据太阳辐射量、气温、日照时长(云量)、风速以及露点温度在内的已知数据，基于热平衡原理建立概化水温公式，即水体净表面热通量与表面温度和平衡温度的差值成正比：

62、

63、式中，为净表面热通量，单位为w/m2；ks为总热量交换系数，单位为w/(m2·℃)，该值为水温和风速的函数；te为平衡温度，单位为℃；tsw为水体表面温度，单位为℃。

64、其中，总热量交换系数ks为：

65、ks＝4.50+0.05tsw+βf(wz)+0.47f(wz)                (22)

66、

67、tm＝(tsw+td)/2                          (24)

68、风函数f(wz)表示为：

69、f(wz)＝9.2+0.46wz2                      (25)

70、式中，β为系数，mmhg/℃；f(wz)在高度为zm处的风函数，单位为wm-2mmhg-1；wz为水面以上zm的风速；td为露点温度，单位为℃；tm为平均温度，单位为℃；

71、在该方程中，平衡温度经验公式为：

72、

73、式中，te为平衡温度，单位为℃；td为露点温度，单位为℃；为太阳短波净辐射通热量，单位为w/m2；ks为总热量交换系数，单位为w/(m2·℃)。

74、步骤6具体如下：

75、步骤6.1、采用静水重构方法求解干湿边界，具体如下：

76、1)基于静水重构法，干湿单元边界边f中心点m处的底坡高程取值为：

77、

78、2)重构两侧水深，同时，使干湿界面处右侧水位与重构后底坡高程相同，即：

79、

80、3)重构界面两侧的流量：

81、

82、在此过程中，为确保重构的底坡高程不高于左侧水位，干湿边界单元边f中心点m处的底坡高程值应取该点重构后底部高程和左侧水位的最低值，即：

83、

84、式中，分别为干湿单元边界边f中心点m左、右侧底坡高程，单位为m；分别为干湿单元边界边f中心点m左、右侧水位，单位为m；分别为干湿单元边界边f中心点m在x、y方向上左、右侧流速，单位为m/s；zbm为干湿单元边界边f中心点m重构后底坡高程，单位为m；分别为重构后左、右侧水深，单位为m；分别为重构后水位，单位为m；分别为重构后在x、y方向左、右侧单宽流量，单位为m2/s；

85、步骤6.2、采用muscl重构法计算单元网格内各变量的空间变化梯度；通过限制变量梯度获得限制变量梯度，基于限制梯度，插值出单元边界中点处的变量值，得到控制单元网格i第k条边边界面中心m的左右变量，以实现muscl二阶重构；

86、

87、由此，可推导出其他变量值：

88、

89、式中，分别为单元网格第k条边边界面中心m在x、y方向上左、右侧的单宽流量，单位为m2/s；和分别为单元网格第k条边边界面中心m在x、y方向上左、右侧底坡高程，水位和水深，单位为m；和分别为单元网格第k条边边界面中心m在x、y方向上左、右侧流速，单位为m/s；

90、步骤6.3、由两步runge-kutta方法获得二阶时间精度，在新时间步长中第i个控制单元网格时间步长n+1时刻的单宽流量值为：

91、

92、中间变量值为

93、

94、式中：为时间步长n时刻的单宽流量增量函数；i为控制单元网格数；ω为第i个控制单元网格的体积，单位为m3；qn+1为时间步长n+1时刻的单宽流量，单位为m2/s，q n为时间步长n时刻的单宽流量，单位为m2/s；δt为时间步长，单位为s；s(qn)为时间步长n时刻的源项。

95、步骤7具体如下：

96、在空间步长δx下，时间步长δt的取值计算公式如下：

97、

98、式中，δt为时间步长，即时间t+1和t之差，s；δxmin表示网格单元中心到对应界面的最小距离，单位为m；u为流速，单位为m/s；g为重力加速度，h为水深，单位为m。

99、本发明的有益效果是，基于gpu加速的全热平衡天然水温模拟方法，是针对当前天然水温模型对复杂河湖海域水温输移模拟精度不高，模拟速度较慢的特点，提出的一种高效高精度的天然水温模拟方法，能够有效模拟河湖海域天然水温输移过程，实现河湖海域二维表面水温的精细化、可视化模拟，以便于更为准确地探究水温对水生态环境的影响。