图正则非负矩阵分解的聚类方法、装置及介质

本发明涉及图像聚类分析，更具体地，涉及一种图正则非负矩阵分解的聚类方法、装置及介质。

背景技术：

1、传统的nmf方法，使用二范数构建初始矩阵，在大多任务中都取得了良好的表现。但是它依旧存在一些局限。其中一个主要的问题是使用二范数构建目标函数，而众所周知的是，二范数对与噪音与异常值是不稳定的。为了获取好的聚类结果，这对于输入的数据有了更高的要求。然而真实世界中，噪音与异常值几乎是不可避免的，即使采取一些方法处理这些异常数据，也会影响聚类的结果。本研究创新性地提出了一种基于图正则化的非负矩阵分解聚类方法，该方法通过精心设计的矩阵优化策略，融入了更为严谨的约束范式，显著增强了算法的鲁棒性。这一改进不仅降低了对初始输入数据质量的严苛要求，即便在数据集中混入异常值时，也能有效抵御其对特征提取过程的干扰，确保结果的稳定性与准确性。因此，该算法在各类实际应用场景中展现出了更为广泛的适用性和潜力，特别是在图像识别领域，如人脸识别任务中，即便面对包含部分异常图片的数据集，依然能够保持卓越的性能，实现高精度的识别效果。

技术实现思路

1、为解决现有技术中存在的上述问题，本发明提供一种图正则非负矩阵分解的聚类方法、装置及介质，通过改进目标函数构造方法，添加更优的约束条件捕捉深层次信息特征，从而，提升了图像分类的鲁棒性与准确性，获得更好的聚类效果。

2、为达到上述目的，本发明采用如下的技术方案：

3、根据本发明的第一方面，提供一种图正则非负矩阵分解的聚类方法，所述方法包括：

4、获取矩阵信息数据以及待聚类数目，所述矩阵信息数据是在推荐系统中代表用户对物品的评分或者用户与物品之间的交互行为，或是在社交网络分析中表示用户之间的互动信息，或是在自然语言处理中，表示词向量与词向量之间的共现关系，或是图片数据灰度化处理后的每个像素点的位置信息与灰度值信息；

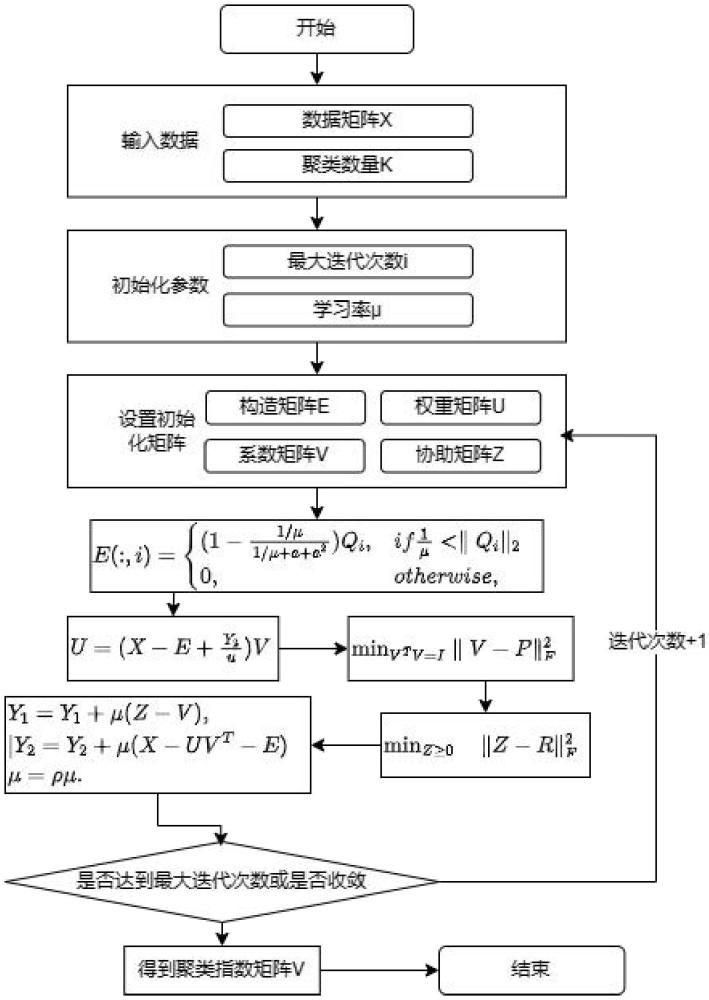
5、定义四个初始化稀疏矩阵，分别对应构造矩阵e、权重矩阵u、系数矩阵v、协助矩阵z，并设定初始的超参数数值μ；

6、确定目标方程与迭代最大次数，根据更新公式迭代求解构造矩阵e、权重矩阵u、系数矩阵v、协助矩阵z、拉格朗日算子y1与y2；

7、在迭代次数最大或者迭代收敛的情况下，输出最终的系数矩阵v，得到聚类结果。

8、进一步地，所述矩阵信息数据表示为x∈rm×n，其中每一个特征值矩阵x由n个列向量xi∈rm组成，rm表示m维空间，m表示样本的维度，n表示样本的数量。

9、进一步地，所述待聚类数目为不超过10的正整数。

10、进一步地，设定的初始的超参数数值μ为0.01。

11、进一步地，所述目标方程表示为：

12、

13、式中，(·)hx表示为∑ilog(1+∥(·)i∥2)，i表示矩阵的行数；

14、tr()表示矩阵的迹；

15、i表示单位矩阵；

16、α、λ1、λ2表示超参；

17、t表示矩阵转置；

18、进一步地，根据数据集的规模、计算复杂度以及计算资源的限制来确定迭代最大次数。

19、进一步地，构造矩阵e、权重矩阵u、系数矩阵v、协助矩阵z的更新公式通过如下步骤得到：

20、将所述目标方程展开得到拉格朗日函数l：

21、

22、并用karush-kuhn-tucker条件获取构造矩阵e、权重矩阵u、系数矩阵v、协助矩阵z的更新公式。

23、进一步地，构造矩阵e的更新公式为：

24、

25、式中，qi表示矩阵q的第i行；

26、权重矩阵u的更新公式为：

27、

28、系数矩阵v的更新公式为：

29、

30、式中，p和w均表示构造矩阵，w＝(vtv+λ2i)-1vt；

31、协助矩阵z的更新公式为：

32、

33、式中，r表示为简化计算而构造的矩阵，z的解为z＝max(r,0)；

34、拉格朗日算子y1与y2以及超参数数值μ的更新公式为：

35、y1＝y1+μ(z-v),

36、y2＝y2+μ(x-uvt-e)

37、μ＝ρμ.

38、式中，ρ表示优化过程中的拉格朗日参数，表示对μ更新的程度。

39、根据本发明的第二方面，提供一种图正则非负矩阵分解的聚类装置，所述装置包括：

40、数据获取模块，被配置为获取矩阵信息数据以及待聚类数目，所述矩阵信息数据是在推荐系统中代表用户对物品的评分或者用户与物品之间的交互行为，或是在社交网络分析中表示用户之间的互动信息，或是在自然语言处理中，表示词向量与词向量之间的共现关系，或是图片数据灰度化处理后的每个像素点的位置信息与灰度值信息；

41、矩阵构造模块，被配置为定义四个初始化稀疏矩阵，分别对应构造矩阵e、权重矩阵u、系数矩阵v、协助矩阵z，并设定初始的超参数数值μ；

42、迭代求解模块，被配置为确定目标方程与迭代最大次数，根据更新公式迭代求解构造矩阵e、权重矩阵u、系数矩阵v、协助矩阵z、拉格朗日算子y1与y2；

43、聚类输出模块，被配置为在迭代次数最大或者迭代收敛的情况下，输出最终的系数矩阵v，得到聚类结果。

44、根据本发明的第三方面，提供一种可读存储介质，所述可读存储介质存储有一个或者多个程序，所述一个或者多个程序可被一个或者多个处理器执行，以实现如上所述的方法。

45、本发明至少具有以下有益效果：

46、本发明通过改进目标函数构造方法，添加更优的约束条件捕捉深层次信息特征，从而，提升了图像分类的鲁棒性与准确性，获得更好的聚类效果。

技术特征：

1.一种图正则非负矩阵分解的聚类方法，其特征在于，所述方法包括：

2.根据权利要求1所述的方法，其特征在于，所述矩阵信息数据表示为x∈rm×n，其中每一个特征值矩阵x由n个列向量xi∈rm组成，rm表示m维空间，m表示样本的维度，n表示样本的数量。

3.根据权利要求1所述的方法，其特征在于，所述待聚类数目为不超过10的正整数。

4.根据权利要求1所述的方法，其特征在于，设定的初始的超参数数值μ为0.01。

5.根据权利要求2所述的方法，其特征在于，所述目标方程表示为：

6.根据权利要求1所述的方法，其特征在于，根据数据集的规模、计算复杂度以及计算资源的限制来确定迭代最大次数。

7.根据权利要求5所述的方法，其特征在于，构造矩阵e、权重矩阵u、系数矩阵v、协助矩阵z的更新公式通过如下步骤得到：

8.根据权利要求1所述的方法，其特征在于，构造矩阵e的更新公式为：

9.一种图正则非负矩阵分解的聚类装置，其特征在于，所述装置包括：

10.一种存储有指令的非暂时性计算机可读存储介质，当所述指令由处理器执行时，执行根据权利要求1至8中任一项所述的方法。

技术总结本发明属于图像分类技术领域，公开一种图正则非负矩阵分解的聚类方法、装置及介质，该方法包括：获取矩阵信息数据以及待聚类数目；定义四个初始化稀疏矩阵，分别对应构造矩阵E、权重矩阵U、系数矩阵V、协助矩阵Z，并设定初始的超参数数值μ；确定目标方程与迭代最大次数，根据更新公式迭代求解构造矩阵E、权重矩阵U、系数矩阵V、协助矩阵Z、拉格朗日算子Y<subgt;1</subgt;与Y<subgt;2</subgt;；在迭代次数最大或者迭代收敛的情况下，输出最终的系数矩阵V，得到聚类结果。本发明通过改进目标函数构造方法，添加更优的约束条件捕捉深层次信息特征，从而，提升了图像分类的鲁棒性与准确性，获得更好的聚类效果。技术研发人员：罗鹏,何郴,胥伟岚受保护的技术使用者：湖南工商大学技术研发日：技术公布日：2024/12/12