风-光-柴-V2G微电网有功频率随机模型预测控制方法与流程

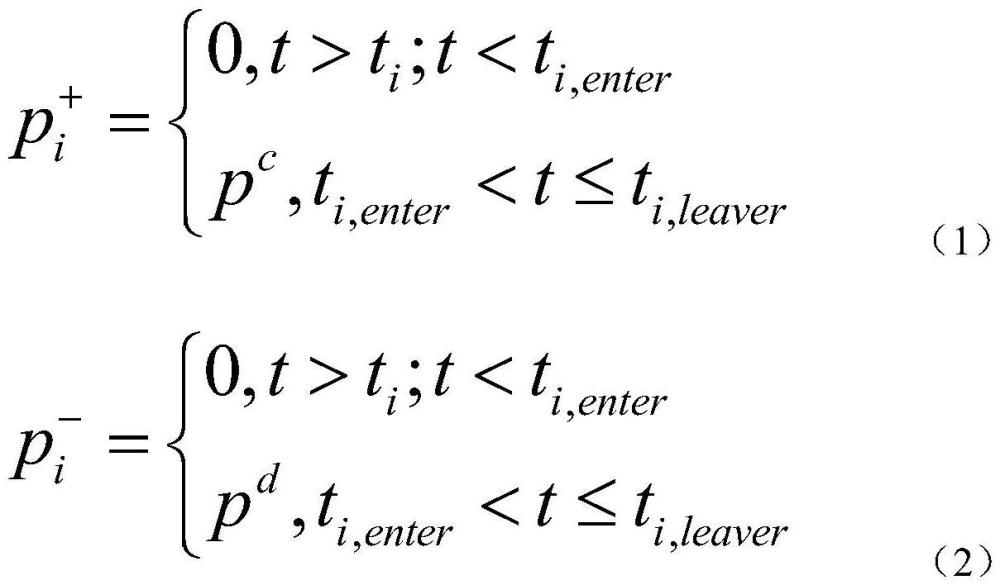
本发明属于微电网频率控制。

背景技术：

1、微电网作为一种规模较小的独立电力系统，主要由太阳能、风能等分布式能源资源以及储能设备构成，具备在特定区域内独立运作的能力。它既可以与主电网相连，也能在必要时独立运行，确保电力供应的稳定性。微电网的主要优点包括利用可再生能源实现能源独立性、提升电力供应的可靠性和灵活性。适用于多种环境，如乡村、岛屿和工业园区等，微电网能够提供清洁、可持续和安全的能源方案。随着新能源的广泛应用，微电网的发展也在加速。同时，电动汽车的普及和储能技术的进步，使得v2g(vehicle to grid)技术受到更多关注。这项技术使电动汽车能够与电网之间实现双向能量交换。这意味着电动汽车不只是电能的消费者，还能将车内电池储存的电能反馈给电网。这种双向的能量流动，让电动汽车成为能源的供应者。

2、为确保微电网的频率稳定，需要设计有效的频率控制器。然而，由于微电网中电源的惯性较小，频率波动较大，且调频能力有限，这成为了工业界面临的一个持续挑战。特别是在风能、太阳能及包含电动车微电网系统中，新能源的发电稳定性不高，随机性大，受天气条件影响较大，难以提供连续稳定的功率输出；同时，电动汽车的充电需求变化较大，导致负荷波动加剧。新能源和电动汽车的这种随机功率波动本身增加了频率的不稳定性，这些随机因素给调频控制的设计带来了极大的难度。在这种高随机性的环境下，传统的频率控制方法效果通常不够理想。

3、专利cn110021960a公开了一种基于模型预测控制的孤岛式微电网电压和频率调控方法。这种控制方法分为三个主要部分：模型预测、滚动优化以及反馈校正。在模型预测环节，它使用基于dq0坐标的滤波器电压和电流状态方程，以及对负载电流的预测。优化目标函数兼顾了孤岛模式下微电网的频率和电压。通过滚动优化过程，方法寻找在预测时间步长内能够最小化电网侧电压和频率偏差的最优控制变量。反馈校正环节则通过采集当前时刻的电网状态来修正预测模型，从而避免由模型不匹配和环境干扰所引起的控制偏差。

4、专利cn115065070a公开了一种应用于微电网的频率控制方法，此方法基于鲁棒h∞控制。微电网环境包含电动汽车充电站和较高比例的可再生能源。由于可再生能源输出的不确定性和负荷波动，维持频率稳定变得具有挑战性。该方法通过设计一种基于h∞控制的中央控制器，来应对微电网内因不确定性引起的频率偏差。通过控制微型燃气轮机，以消除有功输出和负荷间的差异，保持微电网频率在可接受的范围。该控制器的设计特点是基于状态空间模型的频率设计方法，有效解决了模型和扰动不确定性导致的频率稳定问题，具有理论和工程价值。

5、专利cn115333160a公开了一种结合风电机组和电动汽车的微电网鲁棒频率控制方法。这包括基于风电机组的减载控制建立其调频小信号模型，利用能量聚合器构建电动汽车的统一控制模型，以及基于这两个模型建立微电网动态频率响应模型。设计目标是确定性能加权函数和控制加权函数，并使用线性矩阵不等式方法求解h-∞鲁棒频率控制器。此方法有效利用风电机组和电动汽车的调频能力，同时借助h-∞鲁棒控制来抑制不确定性和外部扰动对频率调控的负面影响，减少微电网在功率波动情况下的频率扰动。

6、综上所述，随着风电和光伏发电容量在微电网所占比例上升，其功率受天气等因素影响，呈现出强烈的随机性。同时，电动汽车接入微电网也带来了强烈的随机性。这些随机性的引入给微电网频率控制带来了新的挑战。

技术实现思路

1、本发明的目的是提出一种结合未知输入解耦观测器的有功频率随机模型预测二次频率控制方法来解决微电网频率控制问题的风-光-柴-v2g微电网有功频率随机模型预测控制方法。

2、本发明步骤是：

3、s1、建立考虑ev用户充电需求的充/放电功率模型以及建立含风光柴充电桩的微电网模型s11、单体ev的实时能量与充放电功率的边界与实时状态

4、单体ev的输出功率边界：

5、

6、式中tenter与tleave为ev进入与离开充电站的时间节点，pc与pd为单体ev的充/放电功率；单体ev的能量边界：

7、

8、充电站的整体调控裕度：

9、

10、s12、光伏机组出力概率模型

11、概率密度函数：

12、

13、式中：it为t时段太阳辐射度；μt,σt分别为t时段对数正态随机变量的均值和方差；

14、t时段光伏电站出力ws,t与太阳辐射度it的相关性表示为：

15、

16、式中：istd为标准环境下太阳辐射度；rc为某一特定太阳辐射度；wsr为光伏阵列的额定输出功率；

17、s13、分布式风电机组出力概率模型

18、风速概率密度函数的三参数burr分布函数

19、

20、式中：vt为t时段风速；at,ct,kt分别为t时段burr分布的比例参数、第一形状参数和第二形状参数；

21、t时段风电机组出力ww,t与风速vt的相关性表示为

22、

23、式中：vwr vin vout分别为风机额定风速、切入风速和切出风速；wwr为风机额定输出功率；负荷波动可以用下式所示的正态分布函数来表示

24、

25、其中：σp为负荷有功功率的标准差；μp为有功功率的均值；

26、s14、含风-光-柴-v2g微电网模型的lfc建立

27、s141、柴油机组

28、调速器的传递函数为：

29、

30、式中：kn为调速器增益；tg为调速器时间常数；

31、一阶惯性环节来表示原动机的模型：

32、

33、式中：ky为汽轮机增益；ty为汽容时间常数；

34、原动机与发电机之间的功率关系：

35、

36、式中：δpm为原动机输出的机械功率偏差；δpe为发电机输送给电网的电磁功率偏差；δω为发电机的转子角速度偏差；m为机组的惯性常数；

37、将式(15)进行拉普拉斯变换可以得到频域下的功率关系：

38、δpm(s)-δpe(s)＝msδω     (16)

39、电磁功率偏差δpe与负荷功率偏差δpload之间的关系

40、δpe(s)＝δpload(s)+dδω     (17)

41、式中：δpload为外界负荷扰动；d为负荷阻尼系数；

42、将(16)与(17)联立：

43、

44、s142、风电光伏机组模型

45、控制到输出的传递函数：

46、

47、只考虑风机输入与有功功率输出之间的关系

48、

49、s2、建立改进龙伯格观测器的未知输入观测器

50、微电网模型的状态方程写为如下状态方程形式：

51、

52、其中aob是系统的状态矩阵，bob是系统的控制矩阵，不包含未知扰动项，cob是系统的输出矩阵，eob是未知输入扰动的矩阵，xk是状态向量，yk是输出向量，uk是已知输入向量，dk是等效负载扰动，都是离散化矩阵；

53、状态估计误差向量定义为

54、

55、其中是状态估计值；

56、根据动态系统设计的观测器

57、zk＝f*zk-1+tbuk-1+k*yk    (23)

58、

59、式中：zk为观测器的状态，f、t、k、h为设计的矩阵；

60、扩展得到

61、

62、ek成为一个mek的函数

63、

64、推导出如下方程

65、0＝(hc-i)e     (27)

66、t＝i-hc        (28)

67、f＝a-hca-k1c      (29)

68、k2＝fh       (30)

69、s3、基于场景树随机模型预测控制二次频率优化控制

70、不确定功率的典型场景

71、δp＝{δp1,δp2..........δps}    (31)

72、设当前时刻k根据实际量测数据求得新能源不确定功率为δp(k)＝δpg，将k+1时刻的不确定功率δp(k+1)＝δph作为随机过程建立预测模型，则此过程中的状态转移概率矩阵t(k)中元素δpgh(k)的含义为：在k时刻不确定功率为δpg的条件下，(k+1)时刻不确定功率为δph的概率；

73、将微电网lfc模型，整理为状态空间形式

74、

75、式中：x为状态变量，u为控制变量，d为负荷扰动，y为输出变量；ac，bc，cc，dc分别为连续状态方程的状态常数矩阵，控制常数矩阵，扰动常数矩阵和输出常数矩阵；

76、选取的目标函数形式为二次型

77、j＝min{∑(ζδztrδz)-∑(ζδutgδu)}    (33)

78、式中：式中：ζ为场景树中各场景的概率，r和g为目标函数的加权矩阵；

79、将各个分布式电源的约束条件转换为不等式形式：

80、cuδu(k)≥b(k+1|k)     (34)

81、定义新的变量，即：

82、

83、优化问题就变成了minρtρ，由ρtρ＝(az-b)t(az-b)的极值条件，求导可得极值解为：

84、z*＝(ata)-1atb        (36)

85、k时刻控制序列最优解为：

86、δu*(k)＝kmpc(0-yp(k+1∣k))     (36)

87、

88、取最优控制序列中第一个元素作为输出。

89、本发明主要提出了基于龙伯格观测器的未知解耦输入观测器，实现状态量与未知输入扰动的解耦观测提高观测精度；提出场景树随机模型预测控制器，通过滚动优化和反馈矫正，在考虑各种约束条件利用随机模型预测控制得到最优调频控制量，提高风光负荷不确定条件下的控制效果。所提技术提高了微电网在风光和充电桩不确定性条件下的微电网频率控制效果，帮助分布式风光新能源大规模替代和及电动汽车的进一步普及。