一种飞行器气动特性快速预测方法与流程

本发明涉及飞行器气动特性预测领域，具体地，涉及一种飞行器气动特性快速预测方法。

背景技术：

1、超低轨道指的是平均轨道高度大约介于200km到500km之间的地球轨道。超低轨道卫星可进行高分辨率对地观测，其研制成本也低于常规卫星，具有较高的工程价值和经济效益。相比于传统近地轨道卫星，超低轨道卫星受到的气动力干扰大，减速快，需要进行速度补偿和轨道机动。为了实现卫星姿态控制，需要对其气动特性，特别是阻力系数，做出精确快速的预测。

2、在太空时代的早期，低轨卫星的阻力系数通常使用常数值(比如2.2)进行分析。但是在不同高度使用固定值会引起较大的偏差。超低轨道上的气体已经非常稀薄，按照流动区域划分，属于自由分子流范畴。随着稀薄气体动力学的发展，自由分子流理论可以给出平板、圆球等简单几何外形的阻力系数的解析解。对于实际外形复杂的卫星，阻力系数无法写出解析解，通常采用面元积分法来计算。面元积分法比工程估算中直接取常数值要精确，但是该方法并不能考虑到卫星几何外形之间的遮挡造成的阴影效应以及气体分子在壁面之间的多次反射效应。直接模拟蒙特卡洛方法可以实现三维复杂稀薄气体流动的精确计算，但是计算量巨大，耗费时间很长，无法响应近乎实时的卫星姿态调控需求。试验粒子蒙特卡洛方法最早应用于计算自由分子流条件下的圆管内分子流率。它区别于直接模拟蒙特卡洛方法的特点是，模拟粒子顺序而非同时产生，对计算资源的需求很小，可快速完成计算，同时适用于复杂边界导致的多次反射问题。现有技术为靳旭红,黄飞,程晓丽,王强.超低轨航天器气动特性快速预测的试验粒子monte carlo方法.航空学报,2017,38(5):120625，以及cn105975677a一种复杂外形低轨航天器气动特性的快速预测方法，现有技术成功将该方法应用到低轨卫星气动特性分析领域，取得了积极的效果。不过在具体实现中，现有技术选择圆柱体作为外部计算域边界，试验粒子的初始速度需要在柱坐标系下利用联合概率密度函数采用求逆法和取舍法来确定，形式比较复杂，导致预测效率较低。

技术实现思路

1、针对试验粒子蒙特卡洛方法在模拟超低轨道卫星稀薄气动特性中的问题，本发明提出一种飞行器气动特性快速预测方法，计算流程更加简洁，预测效率较高。

2、为实现上述发明目的，本发明提供了一种飞行器气动特性快速预测方法，所述方法包括：

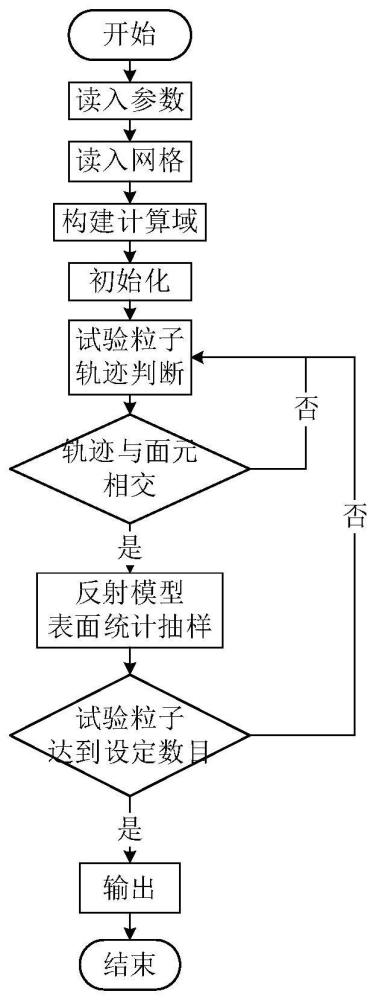
3、步骤1：构建长方体状计算域，飞行器位于计算域内部；

4、步骤2：根据来流条件，在计算域边界处生成试验粒子，试验粒子从边界处进入计算域；

5、步骤3：获得试验粒子的初始位置信息，计算获得碰撞前试验粒子的速度信息，基于试验粒子的初始位置信息和碰撞前试验粒子的速度信息，计算获得试验粒子的第一运动轨迹；

6、步骤4：基于试验粒子的第一运动轨迹，判断试验粒子的第一运动轨迹是否与飞行器表面发生碰撞：若没有发生碰撞，则认为试验粒子飞出计算域，返回步骤2生成新的试验粒子并进行后续步骤；若发生碰撞，则执行步骤5；

7、步骤5：基于气体表面相互作用模型计算获得试验粒子碰撞后的反射速度，基于试验粒子碰撞后的反射速度和碰撞位置，计算获得试验粒子碰撞后的第二运动轨迹，基于试验粒子的第二运动轨迹，判断试验粒子的第二运动轨迹是否与飞行器表面发生碰撞，并继续跟踪试验粒子的后续运动轨迹直至其飞出计算域；可以理解为一直跟踪试验粒子并统计该试验粒子与飞行器表面的所有碰撞，直至该试验粒子飞出计算域；

8、步骤6：针对每个试验粒子，统计每次试验粒子与飞行器表面的碰撞，获得动量和能量交换信息，根据所有试验粒子对应的动量和能量交换信息，计算出飞行器相应的宏观气动特性。本方法中对于每个实验粒子均进行相应的处理方式，相当于有多个试验粒子与飞行器进行碰撞，每次碰撞后处理方式相同。

9、其中，本方法中的轨迹获得方式为：根据牛顿第二定律，知道初始位置，再知道速度和时间，就可以计算出终点位置。

10、其中，本发明考虑到外部计算域形状并不影响最终计算结果，本发明提出采用长方体作为外部计算域边界的思想，不需要在柱坐标系下利用联合概率密度函数采用求逆法和取舍法来确定，可极大简化试验粒子的初始速度的确定过程。

11、优选的，飞行器在xyz三个坐标轴方向的范围分别为：[xmin,xmax]，[ymin,ymax]，[zmin,zmax]，计算域在xyz方向的坐标范围分别为：[xmin-δx×kfactor,xmax+δx×kfactor]，[ymin-δy×kfactor,ymax+δy×kfactor]，[zmin-δz×kfactor,zmax+δz×kfactor]，其中，δx＝xmax-xmin，δy＝ymax-ymin，δz＝zmax-zmin，kfactor为可调参数，kfactor＝0.1～1.0。

12、优选的，所述步骤2还包括计算获得每个试验粒子所代表的真实气体粒子数，具体包括：

13、计算获得试验粒子的入射通量；

14、基于试验粒子的入射通量和计算域各边界面的面积，计算获得单位时间内从各边界面进入计算域的真实气体粒子总数；

15、基于单位时间内从各边界面进入计算域的真实气体粒子总数和试验粒子总数，计算获得每个试验粒子所代表的真实气体粒子数。

16、优选的，试验粒子的入射通量的计算方式为：

17、

18、其中，为试验粒子的入射通量，n为数密度，vmp为基于来流温度的最可几速度，s为速度比，θ为速度矢量与壁面法向之间的夹角，erf为误差函数。

19、优选的，步骤3中碰撞前试验粒子的速度信息的计算方式为：

20、试验粒子的速度在边界面元法向上的投影为u，宏观速度为u0，热速度为u'，u'＝u-u0，β为最可几速度的倒数，sn为法向速度比，sn＝βu0，试验粒子法向速度根据取舍法确定，取舍概率为：

21、

22、其中，p为取舍概率，pmax为取舍概率p的最大值；

23、碰撞前试验粒子的速度在切向上的速度分量的计算方式为：

24、

25、

26、其中，v'和w'分别为碰撞前试验粒子的速度在直角坐标系中v和w方向上速度分量，vmp为基于来流温度的最可几速度，rf1和rf2为0～1之间均匀分布的随机数。

27、优选的，步骤4中飞行器表面采用三角形面元离散处理，基于试验粒子的第一运动轨迹与飞行器表面三角形面元是否相交来判断试验粒子的第一运动轨迹与飞行器表面是否发生碰撞，

28、试验粒子的第一运动轨迹与飞行器表面三角形面元的相交测试采用moller-trumbore算法处理，该算法只需要存储三角形的顶点信息，不需要任何预处理，具有节约内存的优点；

29、三角形面元使用三个顶点v1、v2和v3定义，试验粒子的第一运动轨迹为r(t)，r(t)用点o和归一化方向d表示为：

30、r(t)＝o+td；

31、其中，t是直线方程的参变量；

32、对于三角形面元内的一点t用重心坐标系表示为t(u,v)，t(u,v)表示为；

33、t(u,v)＝(1-u-v)v1+uv2+vv3；

34、当试验粒子的第一运动轨迹r(t)与t(u,v)相交，则有r(t)＝t(u,v)，即：

35、o+td＝(1-u-v)v1+uv2+vv3；

36、整理获得：

37、

38、记e1＝v2-v1，e2＝v3-v1，t＝o-v1，e1为第一参数，e2为第二参数，应用cramer法则获得：

39、

40、整理获得：

41、

42、其中，p和q分别为第一中间参数和第二中间参数，p＝d×e2，q＝t×e1；

43、试验粒子的第一运动轨迹与飞行器表面三角形面元相交，且相交点在三角形面元内的条件为同时满足：t>0、0≤u≤1、0≤v≤1和u+v≤1。

44、优选的，气体表面相互作用模型为漫反射模型。

45、优选的，试验粒子碰撞后的反射速度的计算方式为：

46、

47、

48、

49、其中，u'1、v'1和w'1分别为试验粒子碰撞后的反射速度在直角坐标系中u、v和w方向上速度分量，vmp,w为基于飞行器表面温度的最可几速度，rf1、rf2和rf3为0～1之间均匀分布的随机数。

50、本发明提供的一个或多个技术方案，至少具有如下技术效果或优点：

51、1、计算域采用长方体而非圆柱体，试验粒子的初始速度的确定大大简化，且不影响计算结果的精度。计算域如果采用圆柱体，需要在柱坐标系下利用联合概率密度函数采用求逆法和取舍法来确定，过程比较繁琐。

52、2、试验粒子轨迹与飞行器表面面元的相交测试采用moller-trumbore算法。该算法只需要存储三角形的顶点信息，不需要任何预处理，具有节约内存的优点。