一种融合专家经验的桥梁支座静位移预测方法

本发明涉及桥梁服役状态评估，特别涉及一种融合专家经验的桥梁支座静位移预测方法。

背景技术：

1、支座是连接桥梁上下部构件、传递荷载、调节变形的重要构件，服役期间易遭受环境和荷载变化而发生损坏。支座损坏会改变桥梁结构的受力情况，严重时会对桥面和墩台造成结构性损伤，严重影响桥梁结构的安全性，缩短桥梁的使用寿命。传统支座病害检测存在安全性差、工作量大、效率低等问题，且受观测角度的影响，巡检可能存在死角且主观性较强。近年来，基于数据驱动的支座性能监测及异常预警技术被广泛研究。在桥梁健康监测系统获取海量监测数据的基础上，根据不同类型数据建立桥梁支座运行状态的评估指标，通过比较评估指标与既定阈值可判断支座运行状态，实现支座病害快速检测。相比于传统支座病害检测方法，基于数据驱动的方法成本更低，同时具有泛用性强、灵敏度高的优点。

2、高斯过程回归是一种基于统计理论的非参数概率模型，可有效处理具有高维度和非线性特征的复杂系统建模问题。与传统数据驱动模型相比，高斯过程回归模型具有超参数自适应获取、输出具有概率意义、易于实现等优点，且将额外的观测信息融入至高斯过程回归模型可提高预测精度、降低计算成本。然而，工程中经验丰富的专家可能对一些输入和输出值有经验知识，如温度梯度下支座位移变化率，此类信息描述了模型底层物理规律，但无法直接融入高斯过程回归模型中。贝叶斯-熵方法通过在贝叶斯方程中增加指数项将额外的信息作为约束编码，已被证明可处理多种类型信息。因此，如何基于桥梁健康监测系统采集的主梁温度和支座静位移等长期监测数据，利用贝叶斯-熵方法将专家经验知识编码至高斯过程回归模型，提出一种融合专家经验的桥梁支座静位移预测方法是亟待解决的技术难题。

技术实现思路

1、本发明的目的在于提供一种融合专家经验的桥梁支座静位移预测方法，有效解决上述技术问题。

2、为实现上述目的，本发明采用如下技术方案：

3、本发明一种融合专家知识的桥梁支座静位移预测方法，包括如下步骤：

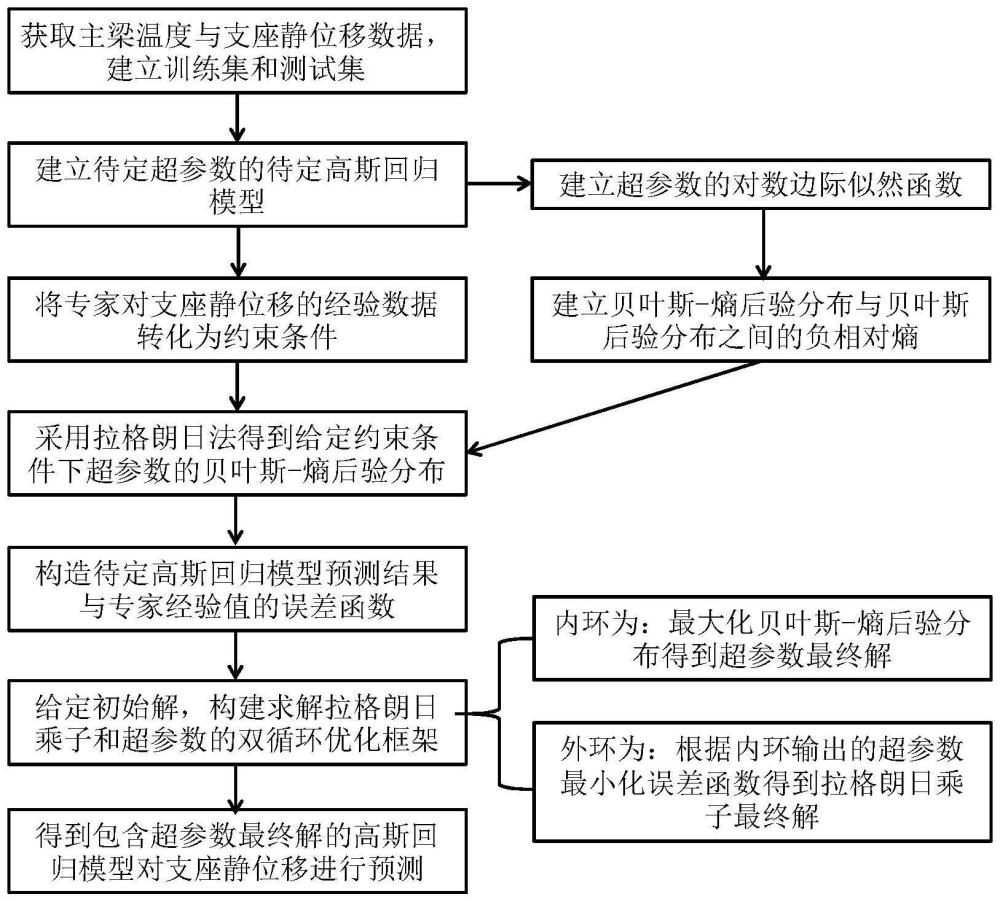
4、步骤一：通过桥梁健康监测系统获取主梁温度与支座位移的监测数据，提取主梁温度数据和支座静位移数据y作为训练集数据d＝(x,y)，假定测试集数据为d*＝(x*,y*)；在高斯过程框架下，根据协方差函数构建训练集中支座静位移预测值f和测试集中支座静位移预测值f*的联合分布，所述协方差函数包含待定超参数θ，根据联合分布得到测试集中支座静位移预测值f*在训练集中支座静位移预测值f下的条件分布，根据联合分布和条件分布推导测试集中主梁温度数据x*时支座静位移预测值f*的后验分布并将该后验分布作为待定高斯回归模型，根据给定主梁温度x和超参数θ下y的条件分布p(y|x,θ)建立超参数θ的对数边际似然函数l(θ)；

5、步骤二：根据超参数θ的贝叶斯先验分布和对数边际似然函数l(θ)得到贝叶斯后验分布p(θ)，将桥梁监测中专家对支座静位移的经验数据转化为数值约束条件和导数约束条件，假定贝叶斯-熵后验分布为pbe(θ)，建立贝叶斯-熵后验分布pbe(θ)与贝叶斯后验分布p(θ)之间的负相对熵，根据所述负相对熵和约束条件构造拉格朗日函数，推导得到给定约束条件下超参数θ的贝叶斯-熵后验pbe(θ；η)；

6、步骤三：任意给定一个拉格朗日乘子的初始解η*和超参数的初始解采用极大后验估计法构造一个度量待定高斯回归模型预测结果与专家经验值误差的误差函数，并构建一个求解拉格朗日乘子η和超参数θ的双循环优化框架，所述双循环优化框架的内环为在给定拉格朗日乘子的初始解η*下最大化贝叶斯-熵后验分布求解超参数θ，所述双循环优化框架的外环为根据内环得到的超参数θ最小化误差函数求解拉格朗日乘子η，经多次循环至误差函数的值小于等于阈值y时求解得到拉格朗日乘子的最终解和超参数的最终解优选阈值y≤0.01；

7、步骤四：将步骤三所得超参数的最终解代入步骤一的待定高斯回归模型中，得到支座静位移贝叶斯-熵高斯过程回归模型，将给定的测试集中主梁温度数据代入支座静位移贝叶斯-熵高斯过程回归模型中对桥梁支座静位移进行预测。

8、需要说明的是，步骤一中，根据主梁温度与支座静位移的训练集数据d＝(x,y)和测试集数据d*＝(x*,y*)，在高斯过程框架下，训练集中支座静位移预测值f和测试集中支座静位移预测值f*的联合分布按式(1.1)确定：

9、

10、式中：f为训练集中支座静位移的预测值向量；μ＝m(x)为训练集主梁温度的均值向量，x为训练集中的主梁温度数据；f*为测试集中支座静位移的预测值向量；p(f,f*)为f和f*的联合分布；μ*＝m(x*)为测试集主梁温度的均值向量；x*为测试集中的主梁温度数据；σ＝k(x,x)为训练集主梁温度数据的协方差矩阵；σ*＝k(x,x*)为训练集主梁温度数据和测试集主梁温度数据之间的协方差矩阵；σ**＝k(x*,x*)为测试集主梁温度数据的协方差矩阵；

11、其中，训练集中支座静位移预测值f的高斯过程先验分布按式(1.2)确定：

12、f＝f(x)～n(μ,σ)                              (1.2)

13、式中：f(x)为先验分布基函数；

14、其中，均值向量μ＝m(x)根据输入维数n定义的多项式基函数按式(1.3)得到：

15、μ＝m(x)＝f(x)β＝[f(x1)···f(xn)]tβ                     (1.3)

16、式中：f(x)为训练集主梁温度数据的基矩阵；x1，···，xn∈x；β为回归系数；

17、其中，回归系数β可根据训练集主梁温度数据和超参数θ通过最小二乘法按式(1.4)确定：

18、β＝(ftσ-1f)-1ftσ-1y                             (1.4)

19、式中：σ-1为σ的逆矩阵；f即f(x)的简化表达；ft为f的转置矩阵；。

20、其中，包含待定超参数θ的协方差函数采用平方指数核函数的形式按式(1.5)确定：

21、

22、式中：k(x,x′)为协方差函数；x和x′为主梁温度的两个输入样本集，例如当x＝x、x′＝x*，则δmn为kronecker函数，当m＝n，则δmn＝1，否则为0；θ＝[σy,l,σn]为超参数的集合(本专利简称超参数θ)，σy,l,σn分别为协方差函数中的方差、长度尺度和噪声方差。

23、需要说明的是，步骤一中，根据高斯过程框架下训练集中支座静位移预测值f和测试集中支座静位移预测值f*的联合分布，测试集中支座静位移预测值f*在训练集中支座静位移预测值f下的条件分布按式(1.6)得到：

24、p(f*|f)～n(μ*+σ*tσ-1(f-μ),σ**-σ*tσ-1σ*)      (1.6)

25、式中：p(f*|f)为测试集中支座静位移预测值f*在训练集中支座静位移预测值f下的条件分布；σ*t为σ*的转置矩阵；σ-1为σ的逆矩阵。

26、需要说明的是，步骤一中，根据测试集中主梁温度数据x*，测试集中支座静位移预测值f*的后验分布服从正态分布n(mt,kt)，其中均值和方差可按式(1.7)、(1.8)计算：

27、mt＝mt(θ；x,y,x*)＝μ*+σ*tσ-1(y-μ)＝m(x*)+k(x,x*)tk(x,x)-1(y-m(x))  (1.7)

28、kt＝kt(θ；x,y,x*)＝σ**-σ*tσ-1σ*＝k(x*,x*)-k(x,x*)tk(x,x)-1k(x,x*)  (1.8)

29、式中：mt＝mt(θ；x,y,x*)为正态分布n(mt,kt)的均值；kt＝kt(θ；x,y,x*)为正态分布n(mt,kt)的方差；θ＝[σy,l,σn]为超参数的集合；k(x,x*)t为k(x,x*)的转置矩阵；k(x,x)-1为k(x,x)的逆矩阵。

30、需要说明的是，步骤一中，所述高斯过程框架中超参数θ的对数边际似然函数l(θ)按式(1.9)确定：

31、

32、式中：l(θ)为高斯过程框架中超参数θ的对数边际似然函数；p(y|x,θ)为给定主梁温度x和超参数θ下y的条件分布(也即y的似然函数)；(y-μ)t为y-μ的转置矩阵。

33、需要说明的是，步骤二中，根据桥梁监测中专家对支座静位移的经验数据，所述数值约束条件和导数约束条件分别按式(2.1)、(2.2)确定：

34、∫mt(θ；x,y,xi)pbe(θ)dθ＝yi       (2.1)

35、

36、式中：pbe(θ)为超参数θ的贝叶斯-熵后验分布；yi为x＝xi处的数值约束(yi为给定主梁温度xi时根据专家经验得到的支座静位移数据)，i＝1,2,3...；为x＝xj处的导数约束(为给定主梁温度xj时根据专家经验得到的支座静位移数据的变化率)，j＝1,2,3...；mt(θ；x,y,xi)为给定主梁温度xi时支座静位移预测值f*的后验分布均值；mt(θ；x,y,xj)为给定主梁温度xj时支座静位移预测值f*的后验分布均值。

37、需要说明的是，步骤二中，所述贝叶斯-熵后验分布pbe(θ)与贝叶斯后验分布p(θ)之间的负相对熵按式(2.3)确定：

38、

39、式中：pbe(θ)为超参数θ的贝叶斯-熵后验分布；p(θ)为超参数θ的贝叶斯后验分布；s[pbe(θ),p(θ)]为pbe(θ)与p(θ)之间的负相对熵；θ为超参数θ的定义域；

40、其中，超参数θ的贝叶斯后验分布p(θ)按式(2.4)确定：

41、p(θ)∝p0(θ)l(θ)        (2.4)

42、式中：p0(θ)为超参数θ的贝叶斯先验分布，常假设θ为非信息先验(即假设p0(θ)为均匀分布)。

43、需要说明的是，步骤二中，根据所述负相对熵和约束条件，所述拉格朗日函数按式(2.5)构建：

44、

45、式中：f[pbe(θ),p(θ),η]为拉格朗日函数；η为拉格朗日乘子，η＝[ηi,ηj]，ηi和ηj分别为i个数值约束和j个导数约束对应的拉格朗日乘子。

46、需要说明的是，步骤二中，根据拉格朗日函数，在给定数值约束条件和导数约束条件下，所述超参数θ的贝叶斯-熵后验分布pbe(θ；η)按式(2.6)确定：

47、

48、式中：pbe(θ；η)为超参数θ在给定约束条件下的贝叶斯-熵后验分布。

49、需要说明的是，步骤三中，采用极大后验估计法，所述度量待定高斯回归模型预测结果与专家经验值误差的误差函数按式(3.1)构造：

50、

51、式中：e为待定高斯回归模型预测结果与专家经验值的误差；为任意给定的超参数的初始解；为给定主梁温度xi、超参数的解时支座静位移预测值f*后验分布的均值；为给定主梁温度xj、超参数的解时支座静位移预测值f*后验分布的均值。

52、需要说明的是，步骤三中，假定所述超参数θ为无信息先验(即假设p0(θ)为均匀分布)，给定拉格朗日乘子初始解η*时，给定约束条件下超参数初始解的贝叶斯-熵后验分布按式(3.2)确定：

53、

54、式中：为给定约束条件下超参数初始解的贝叶斯-熵后验分布；η*为任意给定的拉格朗日乘子的初始解，和分别为给定的i个数值约束和j个导数约束对应的拉格朗日乘子；

55、需要说明的是，步骤三中，所述双循环优化框架的内环为：在给定拉格朗日乘子的初始解η*下最大化贝叶斯-熵后验分布求解得到超参数最终解的过程按式(3.3)进行：

56、

57、式中：为超参数的最终解；η*为任意给定的拉格朗日乘子的初始解；为双循环优化框架中最大化(·)求解θ的函数。

58、所述双循环优化框架的外环为：根据内环得到的超参数θ最小化误差函数求解得到拉格朗日乘子最终解的过程按式(3.4)进行：

59、

60、式中：为拉格朗日乘子的最终解；为双循环优化框架中最小化(·)求解η的函数。

61、需要说明的是，步骤四中，根据步骤三所得超参数的最终解所述支座静位移贝叶斯-熵高斯过程回归模型按式(4.1)确定：

62、

63、式中：为给定测试集中主梁温度数据时支座静位移预测值向量；和分别为所述贝叶斯-熵高斯过程回归模型的均值和方差；

64、其中，均值和方差按式(4.2)、(4.3)确定：

65、

66、

67、式中：为双循环优化框架所得超参数的最终解；为给定测试集主梁温度的均值向量；k(x,x)为训练集主梁温度数据的协方差矩阵，k(x,x)-1为k(x,x)的逆矩阵；为训练集主梁温度数据和给定测试集主梁温度数据之间的协方差矩阵，为的转置矩阵；为给定测试集主梁温度数据的协方差矩阵。

68、与现有技术相比，本发明的有益效果为：

69、1.本发明基于贝叶斯-熵高斯过程模型，将专家知识作为约束编码至支座静位移高斯过程回归模型中，专家经验知识中的物理规律、边界条件等额外信息可以提高高斯过程模型预测精度和外推能力。

70、2.本发明可在主梁温度输入域某一区域样本有限的情况下纳入底层物理规律，将训练样本集划分为多个小的样本集分别建立独立的局部高斯模型，基于贝叶斯-熵高斯过程模型平滑连接多个高斯过程模型，减少构建整个训练集高斯过程模型的训练成本。

71、3.本发明提出一个求解拉格朗日乘子和超参数的双循环优化框架，内环在给定拉格朗日乘子下最大化贝叶斯熵后验求解超参数，外环根据得到的超参数最小化误差函数求解拉格朗日乘子，降低了拉格朗日函数非线性方程组及超参数积分数值逼近的计算复杂度。