基于多尺度损伤-渗流耦合模型的围岩力学参数反分析方法

本发明属于土木工程围岩力学分析，具体涉及基于多尺度损伤-渗流耦合模型的围岩力学参数反分析方法。

背景技术：

1、隧道开挖卸荷会不可避免的对围岩产生损伤作用。损伤具有多尺度特性，宏观上，损伤包括裂隙和节理等；细观上，损伤往往是肉眼不可见的空洞、孔隙、颗粒界面和微裂纹等；微观上，损伤指的是矿物颗粒组分分层面存在的天然缺陷。此外，岩体中赋存有大量的地下水，损伤的演化导致岩体骨架发生变化，影响地下水的渗透特性。因此，从多尺度科学的角度出发，建立岩体损伤-渗流能够更为合理的对围岩稳定性进行评价。

2、复杂岩体模型的参数识别是进行数值分析的难题之一，由于岩体的非均匀性和尺寸效应，实验室测试和现场测试方法具有一定的局限性。采用反分析方法根据岩体变形信息或水头压力的观测数据对模型参数进行修正，能够有效地解决模型工程应用的准确度问题，而基于智能算法的岩体力学参数反分析方法就是其中之一。传统的bp神经网络算法具有收敛速度慢，易陷入局部最优解的问题，引入全局优化算法对网络中的权值和阈值进行全局寻优，能够有效提高模型的预测精度和效率。

技术实现思路

1、本发明为了解决现有技术中的不足之处，提供一种原理更科学、预测精度高、分析效率高的基于多尺度损伤-渗流耦合模型的围岩力学参数反分析方法。

2、为解决上述技术问题，本发明采用如下技术方案：基于多尺度损伤-渗流耦合模型的围岩力学参数反分析方法，包括以下步骤：

3、s1、基于微平面理论，热力学本构方程建立岩体多尺度损伤本构模型；

4、s2、考虑应力场和渗流场的耦合特性，建立渗透系数-体积应变演化方程以及裂隙岩体有效应力方程；

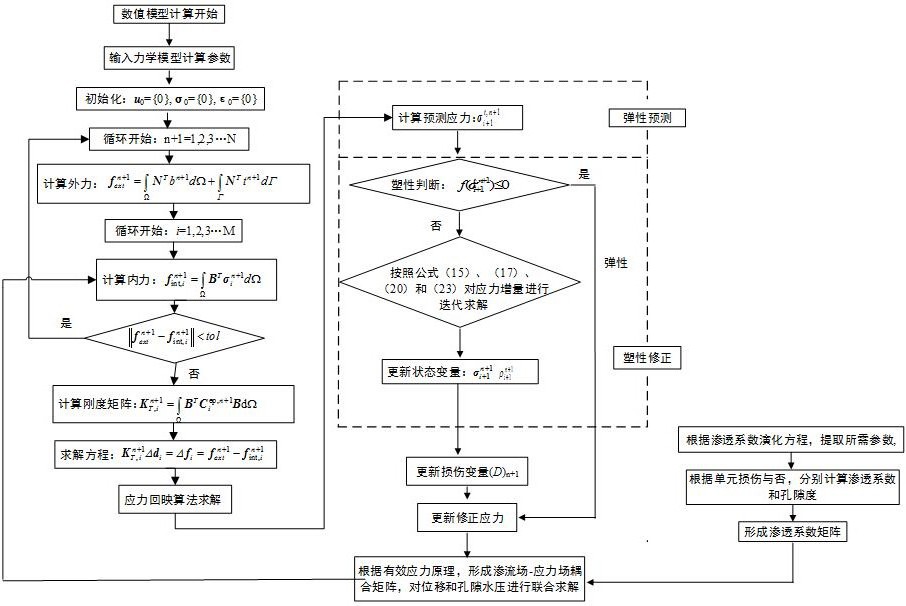
5、s3、基于有限元方法，推导岩体多尺度-损伤本构模型的求解方程；

6、s4、过正交方案设计和有限元计算建立围岩参数反分析样本，输入参数包括：岩石基质弹性模量e0，单位体积裂纹数量ξ，损伤参数k0、η0和kc、ηc，输出参数为围岩拱顶沉降值和拱腰收敛值；

7、s5、利用北方苍鹰算法(northern goshawk optimization，ngo)对bp神经网络的权值和阈值进行寻优，建立ngo-bp模型；

8、s6、利用ngo-bp模型对训练样本进行学习，得到输入参数与输出参数的非线性映射关系，应用该映射关系可以实现对围岩力学参数的反分析。

9、进一步的，步骤s1中岩体多尺度损伤本构模型的屈服函数为：

10、fi(ρi,yi)＝yi-αtr(σ)-k(1+ηρi)           (1)

11、式(1)中：fi为第i个微平面的屈服面；α为塑性参数；tr()为求迹符号；σ为微平面上的应力状态；k和η为损伤参数，裂纹闭合和打开时其分别等于k0和η0，kc和ηc；ρi裂纹密度参数；yi为损伤驱动力，其表达式为：

12、

13、式(2)中：g为rve单元的吉布斯自由能，其表达式为：

14、

15、式(3)中：sm为rve单元中未损伤部分的柔度张量；wi为bazant’s 2×21球面积分方法中的权重；h()为heaviside跳跃函数；ni为四阶张量法向运算符，ti为四阶张量切向运算符。c0和c1分别是裂隙法向和切向上的弹性柔度，其表达式分别为：

16、

17、

18、式(4)和式(5)中：e0和v0分别为完整岩块的弹性模量和泊松比；

19、式(3)中为裂隙面的法向应力

20、

21、式(6)中：为裂隙面的单位法向量；

22、rve单元总应变表达式为：

23、ε＝εe+εd+εin                (7)

24、式(7)中：ε为总应变；εe为rve单元基质中的弹性应变；εd为微裂隙扩展产生得弹性应变；εin为塑性应变。

25、εe＝εe+εd           (8)

26、

27、

28、式(8)和式(9)中：εe为rve单元中总的弹性应变；δ为kroneker符号。

29、进一步的，步骤s2进一步包括以下步骤：

30、s2-1、建立渗透系数-体积应变演化方程，具体如下：

31、

32、式(11)中：n0为初始孔隙率；εv为体积应变；k0初始渗透系数；

33、s2-2、建立多孔介质的有效应力方程，具体如下：

34、σ′＝σ-bpδ            (12)

35、式(12)中：σ′为有效应力张量，压力为正，拉力为负；p为孔隙水压力；1≥b≥0为等效孔隙压系数。

36、进一步的，步骤s3利用有限元方法对模型的数值进行求解，求解过程包括以下步骤：

37、s3-1、求解第n+1个荷载步时的试算应力值，其表达式为：

38、

39、式(13)中：εn为第n荷载步计算得到的总应变值；δεn+1为应变增量；sm为rve单元中未损伤部分的柔度张量；和分别为第n个荷载步下微裂隙扩展产生得弹性应变和基质的塑性应变；

40、s3-2、第n+1荷载步下第k次迭代过程中的应力增量表达式为：

41、

42、其中：为当前迭代步下的εd增量；为当前迭代步下的εin增量；两者表达式分别为：

43、

44、

45、将式(15)和(16)代入(14)可得：

46、

47、式(17)中：

48、

49、式(18)中：sm为完整岩石的柔度张量；pφ的表达式为：

50、

51、rn+1的表达式为：

52、

53、

54、s3-3、对屈服函数(1)进行泰勒展开，只保留一阶项：

55、

56、将式(14)代入式(22)，视裂纹密度增量为未知数，可得

57、

58、通过式(23)可以得到在指定下的裂纹密度增量，然后代入式(15)和(17)可以得到修正应力和塑性应变增量将修正应力带入屈服函数(1)，塑性应变增量带入方程(20)，如果满足下列不等式，则停止迭代并对下一个荷载步进行计算，否则继续进行迭代；

59、

60、

61、式中：tol1和tol2为预设的允许误差值；

62、s3-4、为保证有限元算法中的二次收敛速率，建立一致切屑模量表达式为：

63、

64、s3-5、通过abaqus子程序接口umat和usdfld的联合使用进行实现多尺度损伤-渗流的耦合求解；计算过程中，首先利用umat中独立编写的多尺度损伤本构模型的求解算法，利用abaqus中自带的soil单元进行耦合计算；然后通过usdfld子程序接口提取当前时步计算所得的体积应变εv，利用式(11)对渗透系数进行计算，从而得到渗透系数矩阵和有效应力。

65、进一步的，步骤s4中，在所建立的岩体多尺度损伤-渗流耦合模型基础上，根据训练样本输入参数岩石基质弹性模量e0，单位体积裂纹数量ξ，损伤参数k0、η0和kc、ηc，计算拱顶沉降和拱肩收敛作为样本输出参数。

66、进一步的，步骤s5中利用ngo对bp中的权值和阈值进行全局寻优的具体操作过程包括以下步骤：

67、s5-1、根据输入节点数和输出节点数，按照以下公式确定隐藏层结构：

68、

69、式(27)中：j代表隐含层的节点数；n1和n2分别代表输入层、输出层的节点数，a为0～10的整数；

70、s5-2、随机生成北方苍鹰猎物的初始位置pi，即空间内bp神经网络的初始权值和阈值可以表示为：

71、pi＝xk,i＝1,2,…,n,k＝1,2,…,n(28)

72、s5-3、利用以下方式对北方苍鹰的位置进行更新：

73、

74、

75、式(28)-(30)中：fpi为目标函数值；k是[1,n]范围内不等于i的随机整数；为第一阶段第i只北方苍鹰第j维的新位置；为第i只北方苍鹰的新位置；为更新后第i只北方苍鹰的目标函数值；r和i是[1,n]内的随机数；

76、目标函数值的计算方法如下：

77、

78、式(31)中：n为样本数量，ai为bp神经网络计算出的位移值，bi为所输入样本的位移值；

79、s5-4、北方苍鹰对逃跑的猎物进行快速追击，从而提高ngo算法对搜索空间的局部探索能力；设r表示北方苍鹰的攻击半径，则第二阶段第i只北方苍鹰新位置可以表示为：

80、

81、

82、

83、式(32)-(34)中：t和t为当前迭代次数和最大迭代次数；为第i只北方苍鹰的新位置；为第二阶段第i只北方苍鹰的新位置，为基于第二阶段更新后第i只北方苍鹰的目标函数值。

84、进一步的，步骤s6中通过步骤s4中建立得训练样本对s5中的模型进行训练，得到围岩参数与位移值的非线性映射关系；当输出位移值接近实测位移值时，其所对应得围岩参数即为反分析所得参数。

85、采用上述技术方案，与现有技术相比，针对隧道开挖过程中围岩损伤演化的多尺度问题和损伤-渗流耦合现象，基于微平面理论、连续损伤理论和渗透系数演化方程，本发明所建立得多尺度损伤-渗流耦合模型能够考虑细观裂纹演化和宏观塑性变形对围岩造成得损伤作用；建立渗透系数-塑性应变演化方程以及岩体有效应力方程能够反映出应力场-渗流场的相互耦合作用；推导得有限元求解方程能够实现对模型高效准确的求解；建立得ngo-bp模型能够对bp神经网络中的权值和阈值进行全局寻优，避免陷入局部最优解；最后利用得到的非线性映射关系，能够实现对围岩力学参数的智能反分析。