基于分数阶微积分的全桥LLC谐振变换器的建模分析方法及系统

本发明涉及分数阶全桥llc谐振变换器的建模与分析领域，具体涉及一种基于分数阶微积分的全桥llc谐振变换器的建模分析方法及系统。

背景技术：

1、现有技术中，针对全桥llc谐振变换器常用的建模与分析方法有：基于状态空间平均法的模型、离散迭代映射模型、基于电路原理(kcl、kvl)的分段线性模型以及结合谐波平衡与扰动法的等效小参量法，这些方法的分析对象均是整数阶的开关变换器，即变换器中的电容、电感都是整数阶的元件，然而现有参考文献[1]:“westerlund s.dead matter hasmemory！[m].kalmar,sweden:causal consulting,2002,chap.7.”以及参考文献[2]:“podlubny i.fractional differential equations[m].san diego:academic press,1999,chap.2.”通过对系统中电容和电感的研究发现，在实际应用中，整数阶的电容和电感是不存在的，系统中的电容和电感往往是分数阶的。这就需要为llc谐振变换器建立相应的分数阶模型。

2、现有参考文献[3]:“d.li,k.ding,y.xia and h.dong,research on fractionalorder modeling and piλcontrol strategy of v2g two-stage bidirectionalconverter”与参考文献4“m.f.menke,r.seidel and r.v.tambara,llc led driversmall-signal modeling and digital control design for active ripplecompensation”，可知通过引入扩展描述函数的概念对llc谐振变换器的分数阶模型的建立是有效可行的。

3、现有技术通过对llc谐振变换器建立整数阶模型，对分数阶模型的建立并考虑状态变量分数阶导数的稳态定义问题等方面尚有缺失，无法得到分数阶微积分的全桥llc谐振变换器准确的稳态模型及其小信号模型，难以充分有效地分析全桥llc谐振变换器的分数阶特性和非线性动力学行为。

技术实现思路

1、为解决上述技术问题，本发明提供一种基于分数阶微积分的全桥llc谐振变换器的建模分析方法及系统，该方法能够快速获得分数阶全桥llc谐振变换器稳态模型和小信号模型，及基于分数阶系统的传递函数。

2、本发明采取的技术方案为：

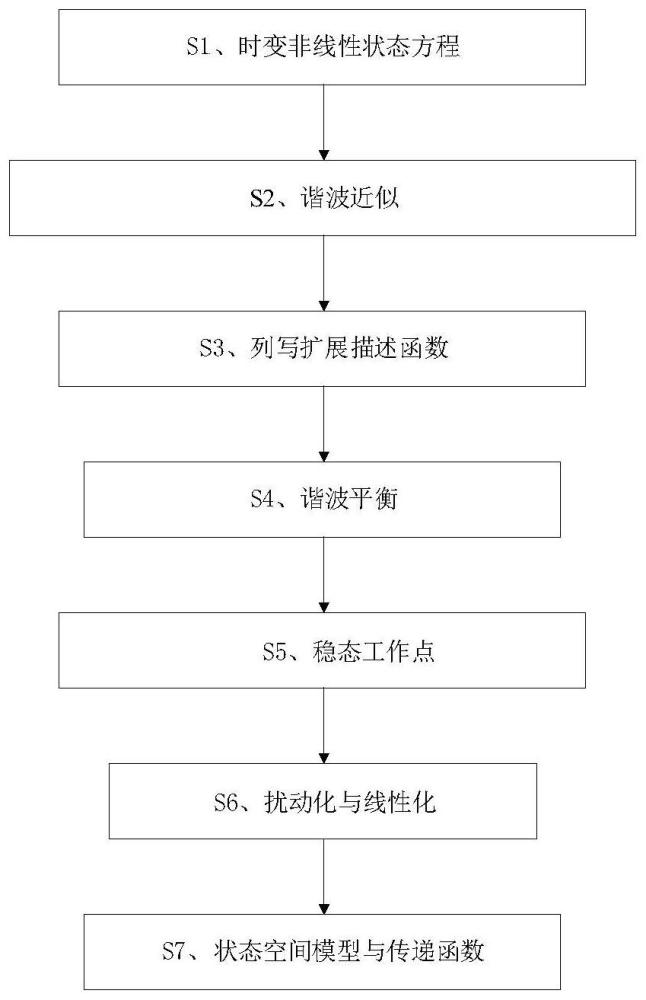
3、基于分数阶微积分的全桥llc谐振变换器的建模分析方法，包括以下步骤：

4、步骤1：将基尔霍夫电压和电流定律应用于分数阶微积分的全桥llc谐振变换器的等效电路中，由于llc谐振元件均为分数阶元件，故其分数阶系统的状态方程描述为：

5、

6、

7、

8、其中，vab表示谐振腔输入电压，lr、cr、lm分别表示为串联谐振电感、谐振电容、并联谐振电感，ir表示流过串联谐振电感的电流，v′se为并联谐振电感电压，为谐振电容电压，im表示流过并联谐振电感的电流，分别为串联电感电压、电容电流和并联电感电压对应时间t的分数阶导数表达式，其中α和β分别用于代表分数阶电感和分数阶电容的阶次。

9、并联电感电压也为变压器原边电压，变压器一次侧与二次侧电压的关系表达式如下：

10、v′se＝nvse＝n*sign(ip)*abs(vse)  (4)；

11、其中，n为变压器变比，vse为变压器二次侧电压，sign(ip)表示串联谐振电感电流ir和并联谐振电感电流im的差值关系表达式，abs(vse)表示变压器二次侧电压幅值。

12、受开关函数影响，其系数矩阵为而变压器次级电流、输出滤波电容电压以及输出电压三者之间的关系表达式如下：

13、

14、

15、r′c＝rc||r    (7)；

16、其中，abs(isp)表示变压器二次侧电流的幅值，isp表示变压器二次侧电流，rc表示滤波电容等效串联电阻，r表示输出端负载电阻，cf表示输出滤波电容，vcf表示输出滤波电容电压，vo表示输出电压，r′c表示等效串联电阻rc和负载电阻r并联，符号“||”表示并联接线。

17、步骤2：将谐振腔的电流和电压波形通过傅里叶级数展开，并用其基频谐波来近似，将周期信号ir、vcr、im分解为正弦分量和余弦分量，描述为：

18、ir(t)＝is(t)sin(ωst)+ic(t)cos(ωst)  (8)；

19、

20、im(t)＝ims(t)sin(ωst)+imc(t)cos(ωst)  (10)；

21、其中，ir(t)表示串联谐振电感电流，is(t)和ic(t)分别为串联谐振电感电流的正弦分量和余弦分量，表示谐振电容电压，vs(t)和vc(t)分别为谐振电容电压的正弦分量和余弦分量，im(t)表示并联谐振电感电流，ims(t)和imc(t)分别为并联谐振电感电流的正弦分量和余弦分量，ωs表示开关角频率，t表示时间。

22、上述状态变量对时间的分数阶导数如下：

23、

24、

25、

26、其中，分别表示串联谐振电感电流、谐振电容电压以及并联谐振电感电流对应时间t的分数阶导数，其阶数为α和β；分别表示串联谐振电感电流、谐振电容电压以及并联谐振电感电流的正弦分量的分数阶导数；分别表示串联谐振电感电流、谐振电容电压以及并联谐振电感电流的余弦分量的分数阶导数，和分别为开关角频率的α次方和β次方。

27、步骤3：建模方法的关键在于用慢变项来表示状态空间方程的非线性。通过扩展描述函数的概念，用基波的正弦和余弦分量来近似非线性项，描述为：

28、vab(t)＝f1(d,vin)sin(ωst)  (14)；

29、式(14)中，vab(t)表示开关网络产生的方波电压，d表示占空比、vin表示输入电压、f1(d,vin)为占空比d和输入电压vin对应的扩展描述函数。

30、sign(ip)*n*abs(vse)＝f2(iss,isp,n*abs(vse))sin(ωst)-f3(isc,isp,n*abs(vse))cos(ωst)  (15)；

31、式(15)中，f2(iss,isp,n*abs(vse))、f3(isc,isp,n*abs(vse))分别表示变量sign(ip)*n*abs(vse)的正弦分量和余弦分量的扩展描述函数；iss、isc分别表示变压器二次电流的正弦分量和余弦分量；isp表示变压器二次侧电流；

32、isp(t)＝f4(iss,isc)  (16)；

33、式(16)中，f4(iss,isc)为isp(t)的扩展描述函数。

34、上述fi(x,y)函数被称为扩展描述函数，它能够通过非线性项的傅立叶展开来计算，结果如下所示：

35、

36、

37、

38、

39、其中：ves为vab基频分量的正弦分量；d为占空比；ips和ipc分别是变压器原边电流ipp的正弦和余弦分量；iss和isc分别是变压器副边电流isp的正弦和余弦分量；vps和vpc分别对应变压器原边电压的正弦和余弦分量。

40、f1(d,vin)表示非线性部分vab(t)的扩展描述函数，f2(iss,isp,n*abs(vse))表示非线性部分sign(ip)*n*abs(vse)正弦分量的扩展描述函数，f3(isc,isp,n*abs(vse))表示非线性部分sign(ip)*n*abs(vse)余弦分量的扩展描述函数，f4(iss,isc)表示isp的扩展描述函数。

41、

42、

43、步骤4：将谐波近似方程：式(11)、式(12)、式(13)和扩展描述函数方程：式(14)～式(20)代入非线性方程组：式(1)～式(7)，将正弦、余弦和直流系数分别对应相等，得到谐波平衡；如下所示：

44、

45、

46、其中：vs和vc分别表示谐振电容电压的正弦分量和余弦分量。

47、

48、

49、

50、

51、

52、步骤5：考虑稳态条件下分数阶全桥llc变换器的新状态变量,根据稳态工作点求得稳态解，按照riemann-liouville定义计算谐振电压电流的导数，在该定义下求得的谐振腔各状态变量以及其他稳态表达式，将其代入到稳态变量方程组中，可得系统状态变量的稳态解，以及其状态空间矩阵。

53、步骤6：将大信号模型围绕稳态工作点进行扰动，并在小信号假设下推导线性化；

54、假设状态空间变量由恒定的直流分量和一个小信号的交流变化组成，对于所有的状态空间变量、输入以及输出信号进行扰动化和线性化，如下所示：

55、

56、其中：x为系统状态变量，x表示状态变量的稳态值，表示状态变量的扰动量。

57、在状态变量的稳态工作点进行扰动化后，通过分离直流项和高阶项进行线性化，得到分数阶全桥llc谐振变换器各状态变量的线性化小信号模型，表示如下:

58、

59、其中：h1、h2、g1、g2、l1、l2、m1、m2、n1、n2分别表示状态变量ωsn、的系数矩阵，表示串联谐振电感电流正弦分量的扰动量，表示串联谐振电感电流余弦分量的扰动量，表示谐振电容电压的正弦分量的扰动量，表示谐振电容电压的余弦分量的扰动量，表示并联谐振电感电流的正弦分量的扰动量，表示并联谐振电感电流余弦分量的扰动量，表示输出滤波电容电压的扰动量，ωsn表示归一化开关角频率的扰动量，表示输入电压的扰动量，表示占空比的扰动量。

60、此外，由h、g、l、m、n、k组成各变量系数表达式的输出电压小信号线性表达式如下所示：

61、

62、其中：表示输出电压的扰动量，k11、k12、k21、k22、k31分别表示扰动量的系数矩阵。

63、步骤7：将求解分数阶全桥llc谐振变换器的小信号模型所得的方程组，用状态空间的方式表示，其状态空间的矩阵方程表示如下：

64、

65、

66、其中各状态变量由矩阵表示，表示输入时忽略控制输入和所有其他干扰输入表示为输出量为a、b、c、d分别为方程组中各变量的系数矩阵，具体如下：

67、

68、

69、

70、其中：t表示矩阵的转置，表示控制输入。表示输出量由输出电压构成。

71、对于线性化系统，通过拉氏变换，可得到控制到输出的传递函数如下：

72、

73、其中：s为拉氏变换过程中象函数的自变量，而原函数的自变量为t，i为7阶单位矩阵。

74、所述步骤s5包括以下步骤：

75、s51、求解谐振变量的稳态值，由riemann-liouville定义可得，分数阶微积分llc谐振变换器中，阶数为α的谐振电容电压与阶数为β的谐振电感电流在稳态时的计算值如下所示：

76、

77、

78、其中：ts表示开关周期，t表示时间，τ表示时间常数，α和β表示分数阶阶数，n表示任意常数，γ(1-α)和γ(1-β)分别表示伽玛函数在参数为(1-α)和(1-β)时的取值。il和vc分别为电感电流和电容电压。

79、s52、求解各变量的稳态解，根据稳态条件下输出滤波电容电压、及变压器副边电压的关系表达式：式(5)～式(7)以及其他各状态变量的稳态方程组：式(23)～式(29)联立，可求得系统状态变量的稳态解，具体如下所示；

80、

81、

82、

83、

84、

85、

86、其中，is、ic、vs、vc、ims、imc分别为状态变量is、ic、vs、vc、ims、imc的稳态值，分别为分数阶开关角频率的稳态值，ves为ves的稳态值，ves为vab基频分量的正弦分量，vin为输入电压vin的稳态值。

87、s53、为了从稳态方程中获得谐振电容电压、谐振电感电流和并联谐振电感电流，将稳态方程组以矩阵形式表示，并形成状态空间矩阵，表示如下：

88、u0＝xy   (47)；

89、y＝x-1u0  (48)；

90、其中：x为各状态变量系数的矩阵，u0、y分别为输出电压以及各状态变量集的矩阵。

91、通过上述步骤可以求得分数阶微积分的全桥llc谐振变换器各状态变量的稳态工作点，其矩阵表达式如下，并可在后续对稳态工作点附近进行扰动化和线性化，详见步骤6。

92、

93、u0＝[ves 0 0 0 0 0]t  (50)

94、y＝[is ic vs vc ims imc]  (51)

95、基于分数阶微积分的全桥llc谐振变换器的建模分析系统，包括以下模块：

96、非线性系统状态方程描述模块，该模块将基尔霍夫电压和电流定律应用于分数阶微积分的全桥llc谐振变换器的等效电路中，由于llc谐振元件均为分数阶元件，故其分数阶系统的状态方程描述为：

97、

98、

99、

100、其中，vab表示谐振腔输入电压，lr、cr、lm分别表示为串联谐振电感、谐振电容、并联谐振电感，ir表示流过串联谐振电感的电流，v′se为并联谐振电感电压，为谐振电容电压，im表示流过并联谐振电感的电流，分别为串联电感电压、电容电流和并联电感电压对应时间t的分数阶导数表达式，其中α和β分别用于代表分数阶电感和分数阶电容的阶次。

101、并联电感电压也为变压器原边电压，变压器一次侧与二次侧电压的关系表达式如下：

102、v′se＝nvse＝n*sign(ip)*abs(vse)  (4)；

103、其中，n为变压器变比，vse为变压器二次侧电压，sign(ip)表示串联谐振电感电流ir和并联谐振电感电流im的差值关系表达式，abs(vse)表示变压器二次侧电压幅值。

104、受开关函数影响，其系数矩阵为而变压器次级电流、输出滤波电容电压以及输出电压三者之间的关系表达式如下：

105、

106、

107、r′c＝rc||r    (7)；

108、其中，abs(isp)表示变压器二次侧电流的幅值，isp表示变压器二次侧电流，rc表示滤波电容等效串联电阻，r表示输出端负载电阻，cf表示输出滤波电容，vcf表示输出滤波电容电压，vo表示输出电压，r′c表示等效串联电阻rc和负载电阻r并联，符号“||”表示并联接线。

109、谐波近似描述模块，在该模块中，将谐振腔的电流和电压波形通过傅里叶级数展开，并用其基频谐波来近似，将这些周期信号分解为正弦分量和余弦分量，描述为：

110、ir(t)＝is(t)sin(ωst)+ic(t)cos(ωst)  (8)；

111、

112、im(t)＝ims(t)sin(ωst)+imc(t)cos(ωst)  (10)；

113、其中，ir(t)表示串联谐振电感电流，is(t)和ic(t)分别为串联谐振电感电流的正弦分量和余弦分量，表示谐振电容电压，vs(t)和vc(t)分别为谐振电容电压的正弦分量和余弦分量，im(t)表示并联谐振电感电流，ims(t)和imc(t)分别为并联谐振电感电流的正弦分量和余弦分量，ωs表示开关角频率，t表示时间。

114、上述状态变量对时间的分数阶导数如下：

115、

116、

117、

118、其中，分别表示串联谐振电感电流、谐振电容电压以及并联谐振电感电流对应时间t的分数阶导数，其阶数为α和β，分别表示串联谐振电感电流、谐振电容电压以及并联谐振电感电流的正弦分量的分数阶导数，分别表示串联谐振电感电流、谐振电容电压以及并联谐振电感电流的余弦分量的分数阶导数，和分别为开关角频率的α次方和β次方。

119、扩展描述函数描述模块，该模块通过扩展描述函数的概念，用基波的正弦和余弦分量来近似非线性项，并描述为：

120、vab(t)＝f1(d,vin)sin(ωst)  (14)；

121、式(14)中，vab(t)表示开关网络产生的方波电压，d表示占空比、vin表示输入电压、f1(d,vin)为占空比d和输入电压vin对应的扩展描述函数。

122、

123、式(15)中，f2(iss,isp,n*abs(vse))、f3(isc,isp,n*abs(vse))分别表示变量sign(ip)*n*abs(vse)的正弦分量和余弦分量的扩展描述函数，iss、isc分别表示变压器二次电流的正弦分量和余弦分量，isp表示变压器二次侧电流。

124、isp＝f4(iss,isc)  (16)；

125、式(16)中，f4(iss,isc)为isp(t)的扩展描述函数。

126、上述fi(x,y)函数被称为扩展描述函数，它能够通过非线性项的傅立叶展开来计算，结果如下所示：

127、

128、

129、

130、

131、其中：ves为vab基频分量的正弦分量；d为占空比；ips和ipc分别是变压器原边电流ipp的正弦和余弦分量；iss和isc分别是变压器副边电流isp的正弦和余弦分量；vps和vpc分别对应变压器原边电压的正弦和余弦分量。

132、f1(d,vin)表示非线性部分vab(t)的扩展描述函数，f2(iss,isp,n*abs(vse))表示非线性部分sign(ip)*n*abs(vse)正弦分量的扩展描述函数，f3(isc,isp,n*abs(vse))表示非线性部分sign(ip)*n*abs(vse)余弦分量的扩展描述函数，f4(iss,isc)表示isp的扩展描述函数。

133、

134、

135、谐波平衡模块，该模块用于将谐波近似方程和扩展描述函数方程代入非线性稳态方程，将正弦、余弦和直流系数相等，得到谐波平衡，如下所示：

136、

137、

138、其中：vs和vc分别表示谐振电容电压的正弦分量和余弦分量；

139、

140、

141、

142、

143、

144、稳态求解模块，该模块用于在稳态条件下分数阶全桥llc变换器的状态变量求取稳态解，按照riemann-liouville定义计算谐振电压电流的导数，在该定义下求得的谐振腔各状态变量以及其他稳态表达式，将其代入到稳态变量方程组中，可得系统状态变量的稳态解，以及其状态空间矩阵；

145、扰动化与线性化模块，该模块用于大信号模型围绕稳态工作点进行扰动，并在小信号假设下推导线性化。假设状态空间变量由恒定的直流分量和一个小信号的交流变化组成，对于所有的状态空间变量、输入以及输出信号进行扰动化和线性化，如下所示：

146、

147、其中：x为系统状态变量，x表示状态变量的稳态值，表示状态变量的扰动量。

148、在状态变量的稳态工作点进行扰动化后，通过分离直流项和高阶项进行线性化，得到分数阶全桥llc谐振变换器各状态变量的线性化小信号模型，表示如下:

149、

150、其中：h1、h2、g1、g2、l1、l2、m1、m2、n1、n2分别表示状态变量ωsn、的系数矩阵，表示串联谐振电感电流正弦分量的扰动量，表示串联谐振电感电流余弦分量的扰动量，表示谐振电容电压的正弦分量的扰动量，表示谐振电容电压的余弦分量的扰动量，表示并联谐振电感电流的正弦分量的扰动量，表示并联谐振电感电流余弦分量的扰动量，表示输出滤波电容电压的扰动量，ωsn表示归一化开关角频率的扰动量，表示输入电压的扰动量，表示占空比的扰动量。

151、此外，由h、g、l、m、n、k组成各变量系数表达式的输出电压小信号线性表达式如下所示：

152、

153、其中：表示输出电压的扰动量，k11、k12、k21、k22、k31分别表示扰动量的系数矩阵。

154、状态空间模型与传递函数求解模块，该模块用于求解分数阶全桥llc谐振变换器的小信号模型及其状态空间矩阵和传递函，其中状态空间的矩阵方程表示如下：

155、

156、

157、其中各状态变量由矩阵表示，表示输入时忽略控制输入和所有其他干扰输入表示为输出量为a、b、c、d分别为方程组中各变量的系数矩阵，具体如下：

158、

159、

160、

161、其中：t表示矩阵的转置，表示控制输入。表示输出量由输出电压构成。

162、对于线性化系统，通过拉氏变换，可得到控制到输出的传递函数如下：

163、

164、其中：s为拉氏变换过程中象函数的自变量，而原函数的自变量为t，i为7阶单位矩阵。

165、稳态求解模块包括以下单元：

166、分数阶导数稳态定义单元，该单元在求解谐振变量的稳态值时用于定义谐振状态变量的稳态值，由riemann-liouville定义可得，分数阶微积分llc谐振变换器中，阶数为α的谐振电容电压与阶数为β的谐振电感电流在稳态时的计算值如下所示：

167、

168、

169、其中：ts表示开关周期，t表示时间，τ表示时间常数，α和β表示分数阶阶数，n表示任意常数，γ(1-α)和γ(1-β)分别表示伽玛函数在参数为(1-α)和(1-β)时的取值。il和vc分别为电感电流和电容电压。

170、稳态值求解单元，该单元用于求解各变量的稳态解，根据稳态条件下输出滤波电容电压、及变压器副边电压的关系表达式以及其他各状态变量的稳态方程组联立，可求得系统状态变量的稳态解。

171、

172、

173、

174、

175、

176、

177、其中，is、ic、vs、vc、ims、imc分别为状态变量is、ic、vs、vc、ims、imc的稳态值，分别为分数阶开关角频率的稳态值，ves为ves的稳态值，ves为vab基频分量的正弦分量，vin为输入电压vin的稳态值。

178、通过上述步骤可以求得分数阶微积分的全桥llc谐振变换器各状态变量的稳态工作

179、状态空间矩阵求解单元，该单元求解稳态矩阵，从稳态方程中获得谐振电容电压、谐振电感电流和并联谐振电感电流，将稳态方程组以矩阵形式表示，并形成状态空间矩阵，表示如下：

180、u0＝xy   (47)；

181、y＝x-1u0  (48)；

182、其中：x为各状态变量系数的矩阵，u0、y分别为输出电压以及各状态变量集的矩阵。

183、通过上述步骤可以求得分数阶微积分的全桥llc谐振变换器各状态变量的稳态工作点，其矩阵表达式如下，并可在后续对稳态工作点附近进行扰动化和线性化。

184、

185、(49)

186、u0＝[ves0 0 0 0 0]t(50)

187、y＝[isicvsvcimsimc](51)。

188、本发明一种基于分数阶微积分的全桥llc谐振变换器的建模分析方法及系统，技术效果如下：

189、1)由本发明所提出的求解方法可知，采用本方法求解基于分数阶微积分的全桥llc谐振变换器的稳态解与小信号模型，相当于将求解非整数阶微积分运算的复杂过程转化为矩阵运算和求线性方程(组)的过程。只要根据基尔霍夫电压和电流定律列写出分数阶全桥llc谐振变换器的系统状态方程，然后通过谐波近似的方式分解为正余弦分量，用扩展描述函数(f1、f2等)表示状态变量的谐波系数，并通过使用非线性项的傅立叶展开来计算这些描述函数，将由谐波近似和edf得到的准正弦项和非线性不连续项代入状态方程，然后分离直流分量、正弦分量和余弦分量的系数，得到一个近似的大信号模型。进一步地，利用该大信号模型得到稳态工作点并进行扰动化和线性化，从而将非线性运算转化为线性运算并求解传递函数。

190、2)相较于过去各种开关电路的建模分析方法，以及数学领域的分数阶微积分求解方法，本发明所提出的求解方法合理的解决了分数阶微积分的全桥llc谐振变换器难以建立准确的小信号模型的特点，将扩展描述函数的概念应用到建模分析过程中，以及考虑了分数阶微积分下谐振状态变量的稳态定义的问题，所得的解具有明显的物理意义，根据采用本发明所提出的方法获得的稳态解以及小信号模型，可以清楚的看到状态变量所包含的谐波成分，有利于对分数阶微积分的全桥llc谐振变换器的动力学特性开展更深入的研究分析。