基于组合赋权法的分布式能源系统多维精细评估方法

本发明属于能源系统分布优化，涉及在以分布式能源系统为主的联供系统建立一个相对客观的多维精细的评估方案，具体涉及一种基于组合赋权法的分布式能源系统多维精细评估方法。

背景技术：

1、分布式能源系统是一种能源供应系统，它与集中生产能源相比，采用联合供应的方式。分布式能源系统能够把二次能源的供应点分散到各个具体的用能地点，甚至延伸到个别住宅。其布局是按照用户需求在附近设置，可以更好地与用户协作，同时也避免了远距离输送和热能损失问题，不再受制于大电网输电损失的限制。分布式能源系统提供的不仅是电力，而且还能够提供加热和/或制冷的能源，是一种多功能能源系统。相较于传统的热电分配系统，它具备灵活的能源供应方式，可以利用多种可再生能源，从而实现环保和可持续发展。尽管分布式能源系统的纯动力装置效率低、成本高，但是它能够充分利用联合生产的优势，从而展现出它的卓越性能。分布式能源系统的另一个重要优点是，它能够确保使用单位的二次能源需求得到充分满足，并且还赋予了使用单位更大的能力来进行调节、控制和保证。

2、然而，供能方式的多样化、分散化也为分布式能源系统的评估带来了困难。因此，对分布式能源系统进行多维精细评估是一个深刻且具有实际意义的课题。以往的研究主要是研究能源系统的某些方面的特性，较少涉及对系统方案做出综合性的、多层次的、精细化的评价。并且较少针对分布式能源系统作相关研究，通常是对单一能源如风电场或其它能源系统如综合能源系统做研究。且在评估体系建立的相关文献中，在指标权重的确立上仍具有较大的主观性。因此，先前对于分布式能源评价方案研究仍然缺乏层次性、精确性。

技术实现思路

1、针对现有分布式能源系统评价方案缺乏层次性、精确性的技术问题，本发明提供一种基于组合赋权法的分布式能源系统多维精细评估方法。本发明为分布式能源系统评价方案设计了一个新的准则层的权重确定思路，该思路能够针对分布式能源系统建立一个相对客观的多维精细的评估方案，从而对于优化能源布局、深化能源分布做出深远影响，从而实现环保和可持续发展。

2、为实现上述发明目的，本发明采用如下的技术方案：基于组合赋权法的分布式能源系统多维精细评估方法，其包括如下步骤：

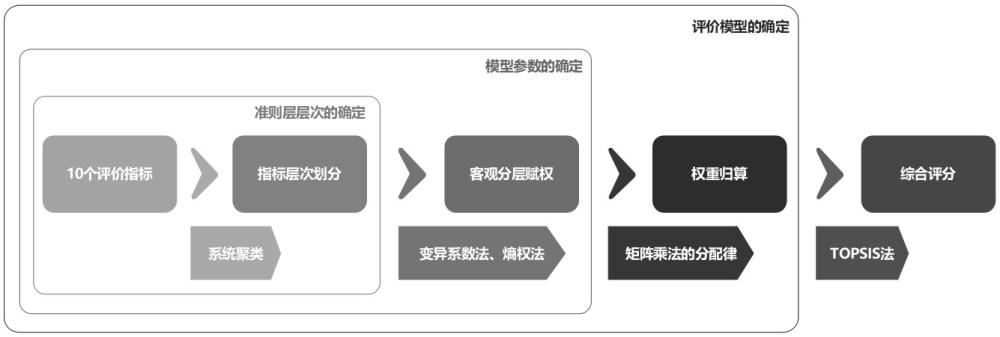
3、步骤一，获取待评估分布式能源系统在“以电定热”模式和“以热定电”模式下任一年中12个月的月度运行数据，并作为评价指标的样本。将该样本中包括电量满足率、能源综合利用率、热电比、供热比、能效㶲效率、毛利润、经济㶲效率、厂用电率、二氧化碳排放量、氮氧化物排放量10个一级指标，通过对应参数的具体应用场景，细分为能源效率、环境性、经济性、可靠性四类二级指标。其中综合能源利用率、热电比、供热比划分为能源效率二级指标，二氧化碳排放量、氮氧化物排放量划分为环境性二级指标，能效㶲效率、毛利润、经济㶲效率、厂用电率划分为经济性二级指标，电量满足率划分为可靠性二级指标，上述分类结果为准则层层次的初步划分结果。

4、步骤二：通过系统聚类法将二级指标“经济性”中的能效㶲效率、毛利润、经济㶲效率、厂用电率进行进一步分析，通过确定最佳聚类数和准则层层次，具体将四个子指标细化为两类，其中能效㶲效率、厂用电率、经济㶲效率划分为弹性经济性，而毛利润划分为刚性经济性。结合步骤一准则层的初步划分结果，得到准则层层次的最终划分结果。

5、步骤三：从步骤二中得到的弹性经济性三个子指标中，通过变异系数法得到三个子指标对应的底层权重，完成相对应的底层至中层的权重设计。

6、步骤四：利用熵权法对除了弹性经济性三个子指标外的剩余指标进行中层与顶层权重设计。其具体步骤包括：对非正向化数据进行指标正向化处理，对正向化后的数据进行标准化；基于正向标准化的数据计算每个指标的信息熵；定义信息效用值，对信息效用值进行归一化，得到各个指标的熵权（即中层至顶层权重与顶层至目标层权重）。

7、步骤五：对已得到的10个原始指标的权重应用topsis法进行总评分，并将总评分图形化，进行对比。

8、进一步地，在步骤二中，在读取数据时，将能效㶲效率、毛利润、经济㶲效率、厂用电率四个指标视为该步骤系统聚类的样本指标，将12个月份视为时间指标。将读取到的数据集记为样本矩阵：

9、

10、其中，代表第个样本指标在第个月份上的值（=1,2,3,4分别表示能源㶲效率、经济㶲效率、毛利润、厂用电率）。

11、由于不同月份的数据差别较大，为了避免数值较大的月份影响到数值水平较小的月份，进行聚类分析之前，采用z-score方法对样本进行标准化，其具体标准化过后的样本矩阵为：

12、

13、其中标准化公式为：， 表示第个样本指标在12个月内的均值，即；表示第个样本指标在12个月内的标准差，即：。

14、进一步地，步骤二中，在标准化样本矩阵之后，采用欧式距离表达样本之间的距离，公式表示如下：

15、

16、其中，表示第p个样本指标，表示第q个样本指标。与分别表示第p个样本指标和第q个样本指标在第j个月正向化后的值。

17、假设第个类有个指标，第个类有个指标，表示两个类中指标的间距，则采用表达两个类之间的距离，公式表示如下。

18、

19、在确定最佳聚类数过程中，将个样本指标划分到个类中，用表示第个类（=1,2,…,），将该类重心的位置记为，则第个类的畸变程度能够表示为：

20、

21、其中表示第个样本指标。

22、由此得到，所有类的总畸变程度即聚合系数：

23、

24、在计算出系统聚类过程中不同聚类数量下的聚合系数后，通过绘制出聚合系数折线图，得到对四个经济性指标聚类的类数；同时利用谱系图（聚类树）识别4个经济性指标的层次关系。经过上述步骤，得到准则层层次的最终划分。具体将四个子指标细化为两类，其中能效㶲效率、厂用电率、经济㶲效率划分为弹性经济性，而毛利润划分为刚性经济性。

25、进一步地，在步骤三基于变异系数法的底层权重设计过程中，极小型指标需要进行正向化处理，而极大型指标不需要进行正向化处理。因此对于极小型指标，运用以下公式进行正向化：

26、

27、其中表示极小型指标中第个样本指标在第个月的数值，表示极小型指标中第个样本指标下12个月的数据的最大值, 表示极小型指标正向化之后的数值。

28、极小型在对极小型指标正向化之后，将极大型指标与极小型指标拼接起来，得到弹性经济性数据的正向化数据矩阵t。

29、为了消除量纲对数据的影响，也为了避免数值水平大的指标的影响覆盖数值水平小的指标的影响，采用标准化的方式对正向化后的数据进行标准化，具体公式如下：

30、

31、其中表示标准化处理后的数据矩阵中的数据，表示正向化处理后的数据矩阵中的数据。

32、变异系数是通过指标的均值和指标的标准差计算得到的。第个正向标准化的样本指标的均值计算方式为：

33、

34、第个样本指标的标准差计算方式为：

35、

36、第个样本指标的变异系数的计算方式为：

37、

38、由此，第个样本指标的底层权重的计算方法如下：

39、

40、在实际应用中，中层指标“弹性经济性”下存在“能效㶲效率”“厂用电率”“经济㶲效率”这多个底层指标，因此采用变异系数法客观地向上赋权。而“毛利润”是“刚性经济性”下的唯一的一个底层指标，因此其底层至中层的权重记为1；剩余一级指标不属于底层指标范围，因此其底层至中层的权重记为1。

41、进一步地，在步骤四利用熵权法进行中层至顶层权重设计中：

42、1.对于除去能效㶲效率、经济㶲效率、厂用电率和电量满足率(电量满足率为可靠性二级指标下的唯一底层指标，因此其中层至顶层权重定为1)的其余底层指标的中层至顶层权重设计：

43、指标正向化（positive transform）采用以下公式：

44、

45、其中, 表示数据矩阵中第m个指标在第j个月的数值, 表示在上述指标中第m个样本指标的在12个月内的最大值，是其余的指标正向化之后的元素，正向化矩阵由构成。

46、数据标准化需要具体分析正向化矩阵的元素特点：

47、(a)当正向化矩阵元素不含负数元素时，采用以下公式进行标准化处理：

48、

49、(b)当正向化矩阵元素包含负数元素时，采用以下公式进行标准化处理：

50、

51、概率矩阵由构成。其中为第个月份下的第个样本指标所占的比重，视为信息熵中的概率，即：

52、

53、由公式可得，保证了每一个月份不同样本指标的概率和为1。其中，表示剩余需要进行熵权法赋值的样本指标数量；

54、在处理信息熵的过程中，假设表示事件可能发生的某一种情况，表示情况发生的概率。在信息熵理论中，信息量与概率呈负相关，且用对数函数表示两者的关系：

55、

56、假设事件g可能发生的情况为：。考虑到信息熵的本质为信息量的数学期望，因此定义事件的信息熵为：

57、

58、其中表示事件g在第h种情况发生的概率。由的轮换对称性或者拉格朗日乘数法能够得知:

59、当时，有最大值。

60、在客观赋权时，将某一个样本指标视为事件，其在不同月份中的取值在该样本指标下的比重视为该事件的不同种情况发生的概率。因此可将视为该指标的信息熵。

61、由此能够得到，第个指标的信息熵为：

62、

63、其中，表示第个指标下第h个情况的概率，即第个指标下第h个月的数值；表示该事件总共发生的不同种情况的数量，即月份数12。

64、第个指标的信息效用值应当和信息量呈现正相关的关系，故将其定义为：

65、

66、由于，因此由上式能够得到，即也是归一化的。

67、得到上述参数之后，对信息效用值归一化，得到各个指标的中层至顶层权重。

68、

69、2.对于弹性经济性指标：

70、将步骤三中得到的正向标准化后的弹性经济性数据与步骤三得到的弹性经济性的底层至中层权重相乘得到弹性经济性指标在不同月份下的得分，即：

71、

72、由于弹性经济性为极大型指标，因此无需进行正向化，只需将得分替换，并进行上述标准化、概率矩阵的计算、信息熵的计算，最后得到弹性经济性的中层至顶层权重。

73、进一步地，在步骤四利用熵权法进行顶层至目标层权重的设计中，定义第个二级指标在第个月的得分为,则的计算公式如下：

74、

75、其中，为第c个二级指标下第m个指标的正向化数据(对于可靠性指标直接使用原始数据)，为二级指标下各个子指标中层至顶层的权重(对于经济性指标为弹性经济性和刚性经济性中层至顶层的权重)。

76、由于各个二级指标均为极大型指标，因此无需进行正向化，只需将替换，并进行标准化、概率矩阵的计算、信息熵的计算，最后得到各个二级指标顶层至目标层的权重。

77、进一步地，在步骤五中，在已经完成底层至中层、中层至顶层、顶层至目标层的权重设置的基础上，利用客观组合赋值进行综合评分。

78、定义为经过正向化和标准化后的数据矩阵, 为第个原始指标位于第级的权重（顶层至目标层视为1级，中层至顶层视为2级，底层至中层视为3级），权重矩阵由构成。

79、定义分布式能源系统的综合得分矩阵为，该矩阵由第j个月的综合得分数据构成具体公式如下：

80、

81、定义第个权重归算值为,且。

82、因此，权重归算值列向量。

83、因此能够得到，相对应的综合得分矩阵=。

84、由综合得分矩阵的推导能够得到，使用权重归算值列向量，将原始数据矩阵和最后的综合得分矩阵连接起来，直观地反映了10个原始指标经过层层赋权后相对于目标层的权重分布。

85、在进行权重归算之后，应用topsis法进行总评分，具体步骤如下：

86、（1）数据预处理，即对数据进行标准化，将“以热定电”“以电定热”两种模式下的12个月度运行数据垂直拼合，形成的24×10的数据矩阵即为topsis评分法所用的数据矩阵。

87、（2）指标正向化，即对得到的24x10的数据矩阵通过正向化处理使所有指标变成极大型指标。如第个指标属于极小型指标，则可基于其所在列的数值按如下方式将其变成极大型指标：

88、

89、正向化后的数据矩阵由上述等式处理后的和本身为极大型指标的数据构成；

90、（3）数据标准化，即消除量纲的影响，采用如下方式将正向化后的数据矩阵标准化得到正向标准化后的数据矩阵，其中表示样本总数，即24个样本：

91、

92、（4）通过计算最值，寻找最优方案与最劣方案。

93、基于正向标准化后的数据矩阵定义最大值：

94、

95、其中，γ表示指标总数，即10个一级指标，定义最小值：

96、

97、（5）计算理想解距离。记第个指标的权重为，即之前求得的权重归算值。权重可以对距离产生畸变，即大的权重会相对地拉长距离，小的权重则会相对地缩小距离。

98、定义第个评价对象与最优方案的距离：

99、

100、定义第个评价对象与最劣方案的距离：

101、

102、（6）计算得分。越接近最优方案的方案应该获得较高得分，越接近最劣方案的方案应该获得较低得分。通过衡量待评价方案与两个极端方案的距离来构造评分：

103、

104、再将得分归一化，得到最终的得分：

105、

106、本发明具有的有益效果如下：

107、本发明从数据本身出发，通过分层聚类、客观组合赋权以及样本差异化评分构建了一个多层次、多维度、精细化的评价方案。该方案基于数据驱动，具有良好的可塑性和可移植性；同时针对分布式能源系统建立了一个相对客观的多维精细的评估方案，从而在深刻理解我国能源布局的基础上为实现双碳目标提供有益贡献。