基于半隐式欧拉算法的粘塑性损伤本构模型数值实现方法

本发明涉及火箭发动机，尤其是涉及一种基于半隐式欧拉算法的粘塑性损伤本构模型数值实现方法。

背景技术：

1、随着大推力液体火箭发动机技术的飞速发展，可重复使用成为新一代液体火箭发动机的一个重要发展目标，而推力室作为火箭发动机中完成推进剂能量转化和产生推力的重要组件，对其使用寿命的研究也十分重要。推力室作为可重复使用火箭发动机的核心部件，在实际应用时，其结构材料往往伴随着与时间相关的非弹性变形。在发动机稳定工作阶段，还可能表现出应变控制条件下的应力松弛现象。此外，推力室在加载过程中的承载能力下降，材料损伤不可忽略。这些材料本构行为会对推力室内壁结构变形的数值模拟结果产生显著影响，进而影响内壁寿命预测的准确性。现有的液体火箭发动机推力室用铜合金本构模型多为弹塑性模型或粘塑性模型，为了开展推力室结构分析和寿命预估等后续研究，进一步建立火箭发动机推力室用铜合金粘塑性损伤本构模型。

2、在建立火箭发动机推力室用铜合金粘塑性损伤本构模型后，通常需要对本构模型进行数值化计算，从而实现本构模型在推力室结构分析中的应用。现有技术中一般利用显式欧拉法和隐式欧拉法进行计算从而求解本构方程，显式欧拉法因受时间步设置的影响，计算并不稳定；而隐式欧拉法实现更为复杂，且由于要迭代计算，计算成本高。这就导致一方面现有技术缺乏针对火箭发动机推力室用铜合金粘塑性损伤本构模型的数值实现方法，另一方面需要克服本构模型数值实现中计算成本高、计算稳定性差的技术问题。

技术实现思路

1、本发明的目的在于提供一种基于半隐式欧拉算法的粘塑性损伤本构模型数值实现方法，以解决现有推力室粘塑性损伤本构模型的数值实现方法缺乏的问题，并缓解计算成本高、计算稳定性差的技术问题。

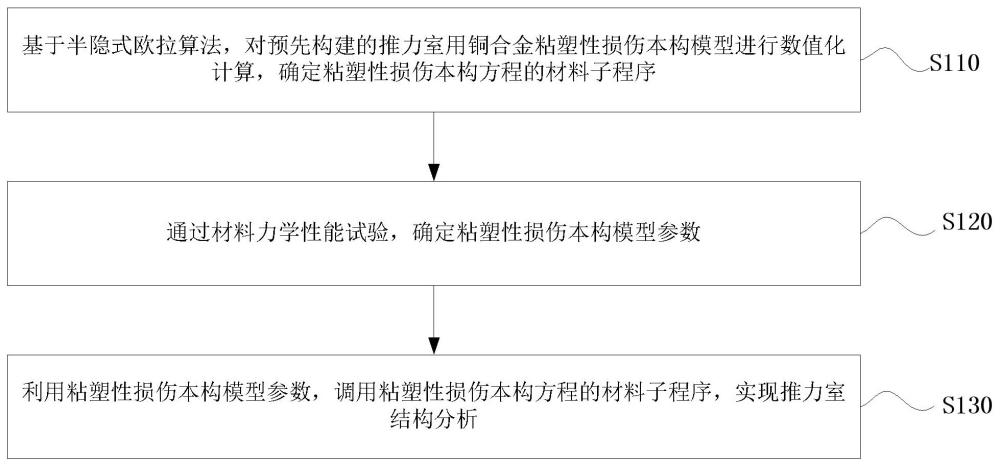
2、第一方面，本发明实施例提供了一种基于半隐式欧拉算法的粘塑性损伤本构模型数值实现方法，包括：基于半隐式欧拉算法，对预先构建的推力室用铜合金粘塑性损伤本构模型进行数值化计算，确定粘塑性损伤本构方程的材料子程序；

3、通过材料力学性能试验，确定上述粘塑性损伤本构模型参数；

4、利用上述粘塑性损伤本构模型参数，调用上述粘塑性损伤本构方程的材料子程序，实现推力室结构分析。

5、在一些可选的实现中，上述预先构建的推力室用铜合金粘塑性损伤本构模型包括以下变量：应力、应变、弹性应变、非弹性应变、屈服函数、累积非弹性应变、背应力上述、各向同性硬化变量和损伤变量；

6、基于半隐式欧拉算法，对预先构建的推力室用铜合金粘塑性损伤本构模型进行数值化计算，确定粘塑性损伤本构方程的材料子程序的步骤，包括：

7、对预先构建的推力室用铜合金粘塑性损伤本构模型中的上述变量按照隐式欧拉格式进行离散，得到当前时间步内的粘塑性损伤本构方程的离散形式；

8、基于上述粘塑性损伤本构方程的离散形式，确定非线性标量方程和一致性切线算子；

9、基于上述非线性标量方程和上述一致性切线算子，确定粘塑性损伤本构方程的材料子程序；上述材料子程序的输入参数包括：当前时刻的应变增量以及上一时刻的热力学变量；上述上一时刻的热力学变量包括：应力，应变，弹性应变，非弹性应变，背应力，各向同性硬化变量，累积非弹性应变和损伤；其中，下标n表示上一时刻，n+1表示当前时刻，n-1表示上一时刻的上一时刻；表示增量。

10、在一些可选的实现中，上述粘塑性损伤本构方程的离散形式包括：

11、总应变：；e表示弹性，in表示非弹性；

12、弹性应变：；e为弹性矩阵；

13、非弹性应变：

14、，其中；nn+1为方向向量，sn+1为偏应力，xn+1为背应力；

15、von mises屈服函数：，其中，为试偏应力；为试应力对应的方向向量；为各向同性硬化律；为屈服强度；；

16、累积非弹性应变率：；

17、随动硬化律：；

18、其中，；ci,γi为材料参数；

19、各向同性硬化律：；b，r∞，q，mr为各向同性硬化相关材料参数；sign(x)=x/|x|为符号函数；

20、损伤演化方程：；为应变能密度释放率；s1、s2和md为模型参数，与材料和温度相关；为由累积非弹性应变表示的损伤阈值，h(x)为heaviside阶跃函数；

21、其中，；σeq为等效应力；为泊松比；σh为静水应力；

22、基于上述粘塑性损伤本构方程的离散形式，确定非线性标量方程的步骤，包括：

23、利用上述弹性应变、上述非弹性应变和上述累积非弹性应变率，生成非线性标量方程；上述非线性标量方程为：

24、；

25、其中，; g是剪切模量。

26、在一些可选的实现中，基于上述粘塑性损伤本构方程的离散形式，确定一致性切线算子的步骤，包括：

27、对上述粘塑性损伤本构方程的离散形式进行微分，得到粘塑性损伤本构方程的微分形式；上述微分形式包括：

28、弹性应变：；

29、非弹性应变：；

30、其中，；符号表示双张量积，为四阶单位张量；

31、von mises屈服函数：；

32、累积非弹性应变率：；和为材料参数；

33、随动硬化律：；其中，；

34、各向同性硬化律：；

35、利用上述粘塑性损伤本构方程的微分形式，生成一致性切线算子；上述一致性切线算子的表达式为：

36、；为四阶偏量运算张量；为一致性切线算子相关张量。

37、在一些可选的实现中，基于上述非线性标量方程和上述一致性切线算子，确定粘塑性损伤本构方程的材料子程序的步骤，包括：

38、利用newton-raphson方法对上述非线性标量方程进行迭代求解，得到当前时刻的累积非弹性应变率；

39、根据上述当前时刻的累积非弹性应变率，确定当前时刻的应变与应力；

40、通过有限元分析软件生成粘塑性损伤本构方程的材料子程序；上述材料子程序的输出为上述当前时刻的应变、应力和上述一致性切线算子。

41、在一些可选的实现中，上述材料力学性能试验包括：单轴拉伸试验、应变控制的循环加载试验、低周疲劳试验和应力松弛试验；

42、通过材料力学性能试验，确定上述粘塑性损伤本构模型参数的步骤，包括：

43、通过材料力学性能试验获得不同温度与载荷下的试验数据；

44、基于上述试验数据，使用粒子群优化算法确定粘塑性损伤本构模型参数。

45、在一些可选的实现中，利用上述粘塑性损伤本构模型参数，调用上述粘塑性损伤本构方程的材料子程序，实现推力室结构分析的步骤，包括：

46、预先构建推力室几何模型，生成推力室结构分析主程序；

47、将上述粘塑性损伤本构模型参数输入上述粘塑性损伤本构方程的材料子程序；

48、将上述材料子程序与上述推力室结构分析主程序结合，实现推力室结构分析。

49、第二方面，本发明实施例提供了一种基于半隐式欧拉算法的粘塑性损伤本构模型数值实现系统，包括：

50、数值化计算模块，用于基于半隐式欧拉算法，对预先构建的推力室用铜合金粘塑性损伤本构模型进行数值化计算，确定粘塑性损伤本构方程的材料子程序；

51、模型参数确定模块，用于通过材料力学性能试验，确定上述粘塑性损伤本构模型参数；

52、结构分析模块，用于利用上述粘塑性损伤本构模型参数，调用上述粘塑性损伤本构方程的材料子程序，实现推力室结构分析。

53、第三方面，本发明实施例提供了一种电子设备，包括存储器、处理器，所述存储器中存储有可在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述第一方面任一项所述的方法的步骤。

54、第四方面，本发明实施例提供了一种计算机可读存储介质，所述计算机可读存储介质存储有机器可运行指令，所述计算机可运行指令在被处理器调用和运行时，所述计算机可运行指令促使所述处理器运行上述第一方面任一项所述的方法。

55、本发明提供了一种基于半隐式欧拉算法的粘塑性损伤本构模型数值实现方法，该方法包括：基于半隐式欧拉算法，对预先构建的推力室用铜合金粘塑性损伤本构模型进行数值化计算，确定粘塑性损伤本构方程的材料子程序；然后通过材料力学性能试验，确定粘塑性损伤本构模型参数；再利用粘塑性损伤本构模型参数，调用粘塑性损伤本构方程的材料子程序，实现推力室结构分析，该方法解决了现有推力室粘塑性损伤本构模型的数值实现方法缺乏的问题，并达到了降低计算成本、提高计算稳定性的技术效果。