一种基于多尺度分析和贝叶斯方法的基坑变形预测方法与流程

本发明属于岩土工程和基坑工程，具体涉及一种基于多尺度分析和贝叶斯方法的基坑变形预测方法。

背景技术：

1、基坑是土木工程中的重要领域，涉及大量岩土工程问题。在基坑施工过程中，由于岩土性质的复杂性和不确定性，基坑变形成为常见的工程问题。准确的基坑变形预测对于工程安全和稳定性至关重要。然而，传统的基坑变形预测方法通常基于宏观尺度的有限元分析或经验公式，缺乏对微观尺度岩土特性的考虑，导致预测精度不高。因此，开发一种基于多尺度分析和贝叶斯方法的基坑变形预测方法具有重要的实际意义和应用价值。

技术实现思路

1、针对现有技术中的上述不足，本发明提供的基于多尺度分析和贝叶斯方法的基坑变形预测方法解决了现有方法预测精度不高的问题。

2、为了达到上述发明目的，本发明采用的技术方案为：一种基于多尺度分析和贝叶斯方法的基坑变形预测方法，包括以下步骤：

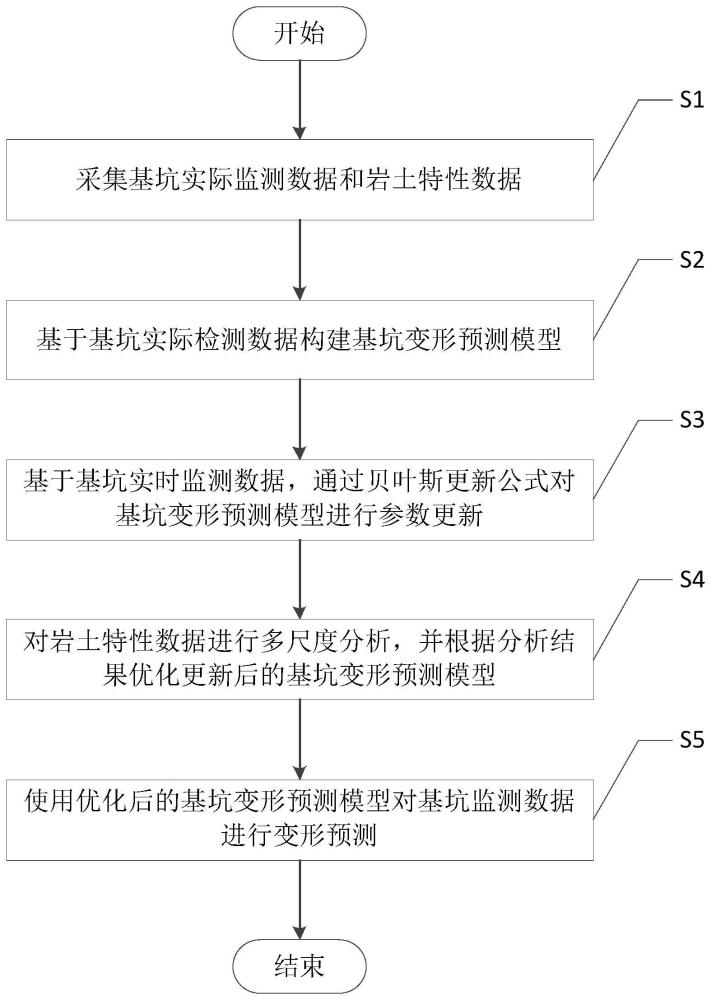
3、s1、采集基坑实际监测数据和岩土特性数据；

4、s2、基于基坑实际检测数据构建基坑变形预测模型；

5、s3、基于基坑实时监测数据，通过贝叶斯更新公式对基坑变形预测模型进行参数更新；

6、s4、对岩土特性数据进行多尺度分析，并根据分析结果优化更新后的基坑变形预测模型；

7、s5、使用优化后的基坑变形预测模型对基坑监测数据进行变形预测。

8、进一步地，所述步骤s2具体为：

9、s21、对基坑实际监测数据依次进行去噪、校准、归一化以及缺失值处理，获得预处理后基坑数据；

10、s22、利用支持向量机将预处理后基坑数据进行信息融合，构建基坑变形预测模型。

11、进一步地，所述步骤s22具体为：

12、s22-1、将预处理后不同源的多维基坑数据形成特征矩阵x，并确定其对应的基坑变形的真实标签，形成目标向量y；

13、s22-2、基于特征矩阵x和目标向量y，利用svm回归模型进行线性回归并进行模型参数优化，形成基坑变形预测模型。

14、进一步地，所述步骤s22-2中，svm回归模型表示为：

15、f(x)＝w·x+b

16、式中，x为特征向量，f(x)为模型输出，w为权重向量，b为偏执项；

17、所述svm回归模型的损失函数为：

18、

19、式中，‖w‖2为权重向量的l2范数，c为正则化参数，ξi和为用于处理数据点偏离ε-tube情况的松弛变量，下标i为表示数据集中的样本索引，用于区分数据集中的每个样本，n为样本数量；

20、所述svm回归模型的待优化模型参数为c和ε，其优化方法包括交叉验证、网络搜索和学习曲线分析。

21、进一步地，所述步骤s3具体为：

22、s31、根据基坑施工进度和变形速率设置基坑变形预测模型的更新频率；

23、s32、根据基坑实时监测数据形成贝叶斯更新公式；

24、s33、根据设置的更新频率，利用贝叶斯更新公式对基坑变形预测模型进行定期参数更新。

25、进一步地，所述步骤s32中，贝叶斯更新公式为

26、p(θ|d)＝p(d)p(d|θ)p(θ)

27、式中，p(θ|d)为基坑实时检测数据的参数θ的后验分布，p(d|θ)为基坑实时监测数据在给定参数θ下的似然函数，p(θ)为参数θ的先验分布，p(d)是基坑实时监测数据的边际概率，其中，参数θ为表征岩土参数复杂分布和不确定性的向量。

28、进一步地，使用mcmc采样方法估计参数θ的后验分布。

29、进一步地，所述步骤s4中进行多尺度分析的方法具体为：

30、对岩土特性数据分别进行微观尺度分析和宏观尺度分析，并根据微观尺度分析结果和宏观尺度分析结果构建耦合模型，利用耦合模型对岩土特性数据进行多尺度分析。

31、进一步地，所述微观尺度分析包括分析土颗粒之间的力学相互作用以及分析土颗粒的力学特性；

32、所述宏观尺度分析包括坑基结构分析及变形分析。

33、进一步地，通过多尺度有限元法和/或多尺度离散元素法构建将微观力学行为和宏观结构行为相互联系起来，并进行参数敏感性分析的耦合模型。

34、本发明的有益效果为：

35、(1)本发明通过高精度传感器和遥感技术采集多源数据，提高了数据的准确性和全面性；

36、(2)本发明利用支持向量机(svm)建立预测模型，实现了不同数据源的信息融合；

37、(3)本发明中引入非参数贝叶斯方法进行参数估计和模型更新，提高了预测的精度和可靠性；

38、(4)本发明综合微观和宏观尺度的岩土特性进行多尺度分析，更加符合实际工程情况；

39、(5)基于本发明方法开发可视化工具，方便用户理解和使用。

技术特征：

1.一种基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，包括以下步骤：

2.根据权利要求1所述的基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，所述步骤s2具体为：

3.根据权利要求2所述的基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，所述步骤s22具体为：

4.根据权利要求3所述的基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，所述步骤s22-2中，svm回归模型表示为：

5.根据权利要求3所述的基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，所述步骤s3具体为：

6.根据权利要求5所述的基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，所述步骤s32中，贝叶斯更新公式为

7.根据权利要求6所述的基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，使用mcmc采样方法估计参数θ的后验分布。

8.根据权利要求1所述的基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，所述步骤s4中进行多尺度分析的方法具体为：

9.根据权利要求8所述的基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，所述微观尺度分析包括分析土颗粒之间的力学相互作用以及分析土颗粒的力学特性；

10.根据权利要求8所述的基于多尺度分析和贝叶斯方法的基坑变形预测方法，其特征在于，通过多尺度有限元法和/或多尺度离散元素法构建将微观力学行为和宏观结构行为相互联系起来，并进行参数敏感性分析的耦合模型。

技术总结本发明公开了一种基于多尺度分析和贝叶斯方法的基坑变形预测方法，包括：S1、采集基坑实际监测数据和岩土特性数据；S2、基于基坑实际检测数据构建基坑变形预测模型；S3、基于基坑实时监测数据，通过贝叶斯更新公式对基坑变形预测模型进行参数更新；S4、对岩土特性数据进行多尺度分析，并根据分析结果优化更新后的基坑变形预测模型；S5、使用优化后的基坑变形预测模型对基坑监测数据进行变形预测。本发明中引入非参数贝叶斯方法进行参数估计和模型更新，提高了预测的精度和可靠性；本发明综合微观和宏观尺度的岩土特性进行多尺度分析，更加符合实际工程情况。技术研发人员：唐堂受保护的技术使用者：四川华腾公路试验检测有限责任公司技术研发日：技术公布日：2024/7/29