一种基于标定数据的傅里叶变换轮廓术三维重建方法

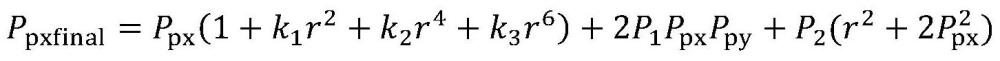
本发明属于计算机视觉/结构光三维重建，具体涉及一种基于标定数据的傅里叶变换轮廓术三维重建方法。

背景技术：

1、结构光三维重建技术被用于精确捕捉物体的空间形状和尺寸，已被广泛应用于多个重要领域；在工业检测中，该技术能够有效评估产品质量并优化生产流程；在医疗成像方面，它提供了详尽的体内三维视图，辅助医生进行诊断和手术规划；此外，结构光三维重建技术还能帮助专家精确复原文物的原始面貌；在虚拟现实与增强现实领域，该技术极大地丰富了用户的互动体验；智能制造领域中，它通过优化自动化生产线的设计与监控，提高了生产效率；材料性能测试领域则依靠这一技术深入分析材料在实际使用环境中的表现；该技术在这些领域的应用不仅显著提升了工作效率，也极大增强了结果的准确性和可靠性。

2、在结构光三维重建领域，特别是在使用傅里叶变换轮廓术(ftp)进行三维形状重建时，现有技术主要通过比较参考平面相位和物体表面相位来计算物体表面的形状。这一技术虽然在多个应用场景中已经得到了广泛的使用，但仍面临着一系列挑战和局限性。

3、典型的ftp需要额外拍摄一张参考平面图像，以用于与物体表面相位进行比较。这一步骤不仅增加了测量流程的复杂性，也增加了时间成本。每次物体与相机-投影仪系统的相对位置发生变化时，都需要重新获取参考平面，这使得测量过程更加繁琐，尤其是在动态或自动化测量环境中。此外，在某些应用场景中，如狭窄空间或特定材质表面的测量，放置和拍摄参考平面可能非常困难，限制了技术的应用范围和灵活性。

4、现有技术中还存在参考平面的准确性和稳定性问题。参考平面的反射性、平整度以及环境光照的变化都可能影响测量精度。频繁的参考平面测量也不利于快速三维重建，增加了操作的繁琐性。

5、综上，尽管傅里叶变换轮廓术(ftp)三维重建技术提供了一种有效的方式来计算物体表面的形状，但因为其需要拍摄参考平面图像的原因，在实际应用中遇到了几个关键的限制和挑战，具体为：

6、1.测量复杂性和时间成本：传统的傅里叶变换轮廓术中必须额外拍摄一张参考平面图像的要求，不仅增加了测量流程的复杂性，同时也延长了整个测量的时间。这对于需要快速响应的应用场景来说，是一个显著的缺点。

7、2.动态测量的挑战：每次物体与相机-投影仪系统的相对位置发生变化时都需要重新获取参考平面。这一要求大大限制了方法的灵活性和适用性，尤其是在进行动态测量或在自动化测量环境中。

8、3.应用场景的限制：在特定的测量环境下，如狭窄空间或特殊材质的表面测量，放置和拍摄参考平面可能非常困难，甚至不可行，这限制了应用范围。

9、4.测量精度的影响：参考平面的准确性和稳定性问题，如反射性、平整度以及环境光照的变化，都可能对测量精度造成不利影响。这对于精度要求较高的应用是一个重大挑战。

10、5.操作的繁琐性：频繁的参考平面测量不利于快速三维重建，增加了操作的繁琐性，降低了工作效率。

技术实现思路

1、针对现有技术的不足，本发明设计一种基于标定数据的傅里叶变换轮廓术三维重建方法，参考平面相位通过直接计算得到，避免传统方法中拍摄参考平面的需要，从而提高三维重建的效率、精度以及便捷性。

2、一种基于标定数据的傅里叶变换轮廓术三维重建方法，具体包括以下步骤：

3、步骤1：标定相机投影仪系统，获取关键几何和畸变参数；

4、所述关键几何和畸变参数包括：相机内参矩阵kc、投影仪内参矩阵kp、旋转矩阵r、平移向量t、相机畸变系数dc、投影仪畸变系数dp、基础矩阵f与本征矩阵e；

5、步骤2：向待测物体投影带黑色标记的正弦光栅图案，并通过相机拍摄图案投影在待测物体的照片；

6、首先生成待投影的正弦光栅图案，其中，图像的水平方向即图像的宽度方向的起始和终止部分各设定n列像素为白色；之后在图案的四角各添加一个s*s像素的黑色方块，作为黑色正方形标记，1/16<s<1/4图像高度，n＝4/5s，完成上述步骤后，使用投影仪将该图案投影到待测物体的表面，并通过相机拍摄图案投影在待测物体的照片；

7、步骤3：计算黑色标记中像素点的空间坐标集合以计算参考平面深度；

8、步骤3.1：提取黑色标记像素点坐标；

9、首先，在相机拍摄的图片中使用多边形逼近算法识别出四个黑色标记的几何形状，然后，对这些识别出的形状进行筛选，选择面积比例与在步骤2生成图案中四个黑色标记相对于整个图案面积的比例最相近的形状，并找到四个黑色标记中每个像素点在相机视角下的齐次二维坐标pc(xc,yc,1)；

10、步骤3.2：计算视差；视差d通过计算xp和xc经过畸变矫正和透视变换后的水平位置差|xp-xc|得到；所述xp表示投影仪视角下黑色标记像素点的x坐标；

11、步骤3.3：计算黑色标记像素点空间坐标；

12、利用视差d和基线b计算黑色标记像素点的空间坐标pw(xw,yw,zw)；

13、基线b通过平移向量t的模长计算得到，其中t1,t2,t3是平移向量的分量；空间坐标pw的计算公式为pc表示四个黑色标记中每个像素点在相机视角下的齐次二维坐标；

14、步骤3.4：计算参考平面深度；

15、参考平面的深度zref为所有计算出的空间坐标pw的z轴坐标的平均值，公式为：

16、

17、步骤4：由步骤1获取的获取关键几何和畸变参数、步骤2生成的正弦光栅图案和步骤3得到的参考平面深度生成正弦光栅图案投影在参考平面上的图像；

18、步骤4.1：归一化相机坐标系的图像点：(x,y,z)t＝inv(kc)·(pcx,pcy,1)t，其中inv()表示矩阵的逆，kc为相机内参矩阵，pcx表示图像坐标系下待测物体的x坐标，pcy表示图像坐标系下待测物体的y坐标；

19、步骤4.2：对归一化的相机坐标系的图像点进行深度调整和透视变换；具体为：

20、将归一化的相机坐标系中的图像点利用参考平面的深度zref进行深度调整，然后，应用旋转矩阵r和平移向量t将调整后的点转换到世界坐标系：

21、(x′,y′,z′)t＝r·(zref·(x,y,z)t)+t

22、步骤4.3：将转换为世界坐标系的三维点(x′,y′,z′)t投影到投影仪图像平面上，并将其齐次坐标转换为笛卡尔坐标：

23、(u,v,w)t＝kp·(x′,y′,z′)t

24、

25、其中，kp为投影仪内参矩阵，(u，v，w)t是三维点(x′,y′,z′)t投影到投影仪图像平面上的齐次像素坐标；(ppx，ppy)是将齐次像素坐标(u，v，w)t转换为笛卡尔坐标系中的二维像素坐标；

26、步骤4.4：对投影仪图像平面的笛卡尔坐标进行畸变矫正；应用径向和切向畸变矫正，得到最终的投影坐标(ppxfinal,ppxfinal)；

27、

28、

29、其中，r表示相机图像平面中的点到畸变中心的距离，k1,k2,k3是径向畸变系数，p1,p2是切向畸变系数；

30、步骤4.5：对步骤4.1-4.4中对相机视角下的坐标的处理使用一个映射矩阵m来代替表示，基于映射矩阵生成正弦光栅图案投影在参考平面上的图像；

31、对步骤2中生成的正弦光栅图案图像i使用映射矩阵m进行重映射，得到图像iref；i中的每个像素点(x,y)经过重映射后，就得到了iref中对应像素点坐标(x′,y′)：

32、(x′,y′)＝m(x,y)

33、由此，计算出了正弦光栅图案投影在参考平面上的图片，该图片中正弦光栅条纹分布记为：

34、iref(x,y)＝a(x,y)+b(x,y)cos[2πf0x+φref(x,y)]

35、其中，a(x,y)为背景光强，b(x,y)是条纹对比度，f0是正弦光栅条纹的空间基频，φref(x,y)是包含参考平面高度信息的相位分布；

36、步骤5：应用傅里叶变换轮廓术提取包含待测物体高度信息的相位信息；

37、步骤2中待测物体表面的正弦光栅分布信息，表达为：

38、iobj(x,y)＝a(x,y)+b(x,y)cos[2πf0x+φobj(x,y)]

39、步骤4中参考平面的正弦光栅分布信息，表示为：

40、iref(x,y)＝a(x,y)+b(x,y)cos[2πf0x+φref(x,y)]

41、其中，a(x,y)为背景光强，b(x,y)是条纹对比度，f0是正弦光栅条纹的空间基频，φobj(x,y)和φref(x,y)分别是包含物体和参考平面高度信息的相位分布；

42、所述包含物体高度信息的相位分布φobj(x,y)，具体为：

43、首先计算待测物体表面的正弦光栅分布信息；

44、iobj(x,y)＝a(x,y)+b(x,y)cos[2πf0x+φobj(x,y)]

45、将其改写为：

46、gobj(x,y)＝iobj(x,y)＝a(x,y)+c(x,y)exp(2πif0x)+c*(x,y)exp(-2πif0x)，

47、其中c*(x,y)为c(x,y)的共轭复数；i是虚数单位，i2＝-1；

48、对gobj(x,y)做一维傅里叶变换并使用带通滤波器进行滤波得到基频分量，再对其进行傅里叶逆变换得到复数形式的相位信息c(x,y)，包括幅度和相位；

49、通过对c(x,y)的实部和虚部进行反正切求出包裹相位，im[·]和re[·]表示取复数实部和虚部：

50、

51、所述包含参考平面高度信息的相位分布φref(x,y)与得到包含物体高度信息的相位分布φobj(x,y)的过程相同；

52、最后，通过itoh相位解包裹算法处理φobj(x,y)和φref(x,y)，得到解包裹相位φuobj(x,y)和φuref(x,y)，将φuobj(x,y)减去φuref(x,y)获得包含待测物体表面高度信息的绝对相位值δφu(x,y)；

53、步骤6：利用三角测量原理计算相机捕获的待测物体照片中像素点的空间坐标，从而获取三维形貌信息；

54、步骤6.1：利用绝对相位计算投影仪视角下的待测物体像素点x坐标：

55、通过步骤5得到的绝对相位，计算在投影仪视角下，待测物体像素点x坐标xpobj，这是通过将相位变化转换为空间位置变化来实现的：

56、

57、其中，f0是投影仪使用的正弦结构光的频率；

58、步骤6.2：通过计算待测物体像素点在投影仪视角xpobj和相机视角下坐标xc经过畸变矫正和透视变换后的水平位置差来得到视差d’；视差d’的计算公式为：

59、d’＝|xpobj-xc|

60、步骤6.3：利用视差d’和相机的焦距f，计算待测物体表面的高度zobj；高度计算公式为：

61、

62、待测物体表面的三维点表示为pobj(xobj,yobj,zobj)，其中xobj和yobj分别对应于步骤2中相机捕获的图像上待测物体像素点的x和y坐标。

63、本发明有益技术效果：

64、本发明直接计算参考平面相位：传统的三维重建方法需要额外拍摄参考平面图像，本发明通过标定数据直接计算参考平面相位，省去了额外拍摄的步骤，大幅度简化了测量流程，提高了测量效率。使用带黑色正方形标记的正弦光栅图案：本发明采用的带黑色正方形标记的正弦光栅图案，提高了参考平面深度计算的准确性和稳定性，从而提高了最终三维重建的精度。适用于动态测量：本发明的方法不需要每次物体与相机-投影仪系统相对位置发生变化时重新获取参考平面，使其非常适合动态或自动化测量环境。优化的数据处理流程：通过对数据处理流程的优化，本发明能够在保证高精度的同时，减少数据传输量，提高了同步效率。

65、本发明的方法不受待测物体与相机-投影仪系统相对位置变化的影响，适用于动态或自动化测量环境，且能够在狭窄空间或特殊材质表面等特定测量环境下有效进行，极大地拓宽了应用范围。由于本发明方法的高效性、高精度和简便性，它适用于多种不同的测量环境，包括那些对速度和精度有严格要求的场合。提高了测量效率：通过直接计算参考平面相位，省去了传统方法中需要的额外拍摄参考平面图像的步骤，大大简化了测量流程，从而显著提高了测量的效率。提升了测量精度：采用带有黑色正方形标记的正弦光栅图案，以及优化的数据处理流程，确保了高度准确和稳定的参考平面深度计算，进而提升了三维重建的精度。减少了数据传输量，提高了同步效率：本发明优化的数据处理流程减少了数据传输量，提高了数据同步的效率，特别适用于数据量大或对实时性要求高的应用场景。