一种基于最优时间重用机制的动态多AGV路径规划方法

本发明涉及agv分拣系统中的路径规划，具体是一种基于最优时间重用机制的动态多agv路径规划方法。

背景技术：

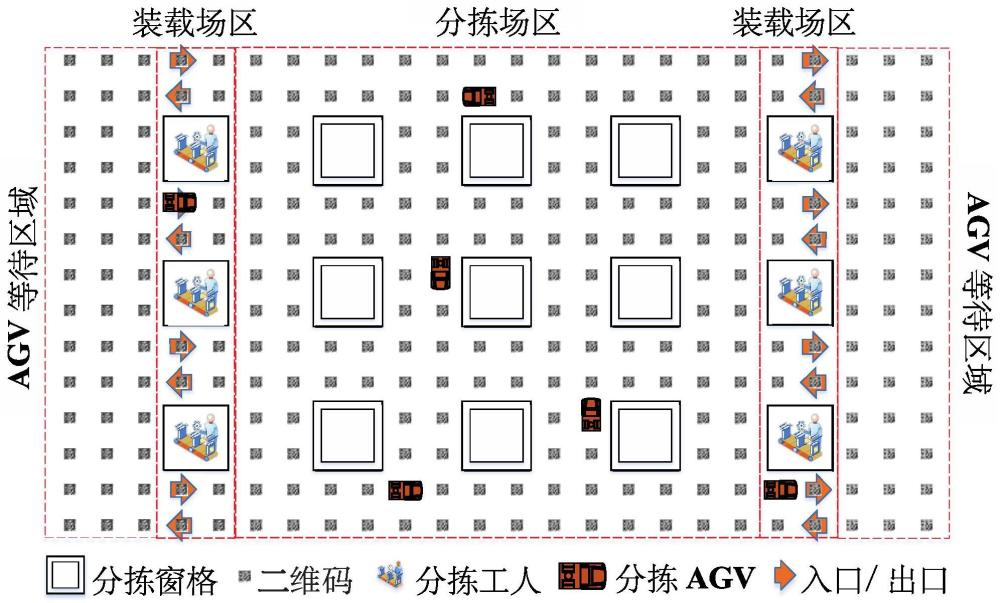
1、作为一种新型的分拣方法，agv分拣系统由于其高度的灵活性，成本效益和强大的鲁棒性，在物流行业中受到了广泛的关注。在agv分拣系统中的路径规划问题是一个具有大量agv同时运行的两阶段路径规划问题。在agv分拣系统中，agv从装载点将快递包裹运输到目标点，然后离开分拣区域。因此，为多个连续的分拣任务(即解决动态路径规划问题)规划短且无冲突的路径对于提高agv分拣系统的效率至关重要。然而，这个问题存在很大的挑战。首先，路径规划问题是np难的，使得在有限的时间内无法获得最优解。其次，任务是动态的并且不断添加，导致现有路径的频繁失败。最后，每个任务涉及一系列必须按序访问的目标点，而不是单个点。传统的路径规划方法无法在单个过程中为一系列目标点规划路径。

2、传统方法大多采用窗口策略来解决动态规划问题。具体来说，基于指定的窗口长度，将动态路径规划问题分为多个连续的静态(一次性)路径规划问题。然后使用选择的一次性规划方法来解决这些问题。窗口策略包括两个关键参数：重规划周期和无冲突路径长度。重规划周期是连续两次路径规划过程之间的时间间隔。无冲突路径长度指定了必须解决冲突的路径的范围，作为规划器对路径轨迹的预见性的指标。这两个参数不仅对系统产生各种影响，而且还相互影响。因此，为这两个参数选择最合适的值对于最小化系统效率变得至关重要。然而，由于它们对任务执行的间接影响，确定这些参数与任务完成率之间的函数关系复杂而具有挑战性。根据对这两种参数的使用方法不同，现有动态路径规划策略主要分为三种类型：第一类方法在每次出现新任务时重新规划路径。重规划周期由新任务的出现确定，无冲突路径长度为无限，便于在每个重规划周期内规划完整的路径。然而，这种方法导致了统一路径的过度重复规划，导致了大量的等待和浪费时间。第二类方法利用增量规划来避免由过多的计算时间引起的低效率。这些方法只基于现有的路径来规划部分路径。重规划周期和无冲突路径长度与第一种类型相同。然而，这些方法关注局部优化，不能有效地保证最优性，特别是在有大量冲突的情况下。第三类方法通过同时执行路径规划过程和agv运动过程，避免了计算时间的浪费。这些方法根据经验设置了一个重规划周期和无冲突路径长度。预设的参数值保持恒定，无论系统处于不同状态时的计算需求如何。这种方法使用物理系统的操作时间进行路径规划，从而提高了系统效率。然而，这种方法没有考虑物理系统的操作时间和算法的求解时间之间的匹配程度。这可能会导致路径优化不足和超时等待，从而导致提升有限。本发明着重考虑使算法进行路径规划的求解时间与物理系统中agv的移动时间相匹配起来，提出一种基于最优时间重用机制的动态多agv路径规划方法，保证在避免超时计算所导致的停车等待的同时尽量优化路径，从而提高整个系统的分拣效率。

技术实现思路

1、本发明提出了一种基于最优时间重用机制的动态多agv路径规划方法，是在充分考虑匹配系统求解时间和agv移动时间的要求下提出的。首先是在整体层面上，通过对分拣区域内的agv数量的理论分析和对路径最优性和计算时间的拟合，选择合适的重规划周期；其次在单次规划中，根据对不同算法的计算时间拟合，选择最合适的无冲突路径长度；最后通过临时目标点选择算法将无冲突路径长度转换为可行的临时目标点，以适应不同的单次路径规划方法。通过以上三个步骤来实现此方法。

2、本发明为实现上述目的所采用的技术方案是：

3、一种基于最优时间重用机制的动态多agv路径规划方法，包括以下步骤：

4、1)根据agv的进入速率，对agv驶入和驶出量进行分析，选择使任务完成速率最大的重规划周期；

5、2)在具体每次的规划中，选择在限定的求解时间内能够最大程度优化路径的无冲突路径长度；

6、3)针对不同的单次路径规划方法，基于无冲突路径长度生成临时目标点。

7、所述步骤1)包括以下步骤：

8、1.1)基于支持向量机svm数据拟合模型，利用agv驶入驶出速率，分别得到路径最优性预测值hp、agv数目na以及路径规划求解时间预测值tp；

9、1.2)分析预测任务完成速率；

10、1.3)选择重规划周期长度，使任务完成速率最大化。

11、所述步骤1.1)包括以下步骤：

12、1.1.1)对路径最优性和分拣区域内agv数目进行预测：

13、[hp,na]＝fh-n(α,β,t/δt)

14、

15、hp＝max(fh(α,β,na,t/δt),1)

16、其中，hp表示路径最优性的预测值，na表示地图中的agv数目，α和β为分拣系统中的地图尺寸，分别表示地图的行数和列数，t是重规划周期时长，δt是agv移动单位距离所花费的时间，t/δt是当前所设定重规划周期内agv可以移动的步数，fh-n(·)表示几种参数之间的函数关系，dmean为分拣区域的平均任务长度，η为每个周期进入分拣区域的agv数目，fh(·)表示基于svm的路径最优性拟合模型；

17、1.1.2)对求解时间进行预测：

18、tp＝ft(α,β,na,t/δt)

19、tp表示求解时间的预测值，ft(·)表示基于svm的求解时间拟合模型。

20、所述步骤1.2)包括以下步骤：

21、1.2.1)估计实际重规划周期长度：

22、

23、其中，是对重规划周期的实际值进行预测，t是重规划周期的预先设置值，tp是所预测的求解时间；

24、1.2.2)估计在每个周期中实际进入分拣区域的agv数目：

25、

26、其中，ηp表示每个周期中实际进入分拣区域agv数目的估计值,ri是任务出现速率，ni是分拣区域中的入口数目；

27、1.2.3)计算每个步数的任务完成速率估计值：

28、

29、其中，是对应于重规划周期内可移动的步数i的任务完成速率。

30、所述步骤1.3)包括以下步骤：

31、1.3.1)从1到遍历任务步数i，得到所有对应的

32、1.3.2)从所有的中选择最大的值所对应的i中最小的值；

33、1.3.3)将选取的步数k与agv移动单位距离需要花费的时间δt相乘，得到所设定的重规划周期t：

34、t＝k*δt。

35、所述步骤2)包括以下步骤：

36、2.1)预估下一周期分拣区域内的agv数量：

37、根据agv与目标点之间的曼哈顿距离判断，如果此距离大于无冲突路径长度备选值，则此任务会保留至下一周期；反之，此任务不会保留至下一周期；然后统计出有多少任务将会保留至下一周期；再加上下一周期可能新进入分拣区域的agv的数量的最大值，即每个入口进入一辆agv，作为所预测的下一周期分拣区域内agv数量n；

38、2.2)根据求解时间拟合模型选择无冲突路径长度：

39、设置作为无冲突路径长度的选择区间，在该区间中，根据基于svm的求解时间拟合模型，找到求解时间小于预设周期t的最大步数作为所选择的无冲突路径长度l。

40、所述步骤3)具体为：

41、情况1：单次路径规划方法可以直接根据无冲突路径长度进行部分路径规划：

42、针对该情况，如果能够规划连续的多个目标，即目标点和出口，则直接将无冲突路径长度设置为l，进行路径规划；如果无法规划连续的多个目标，对于分拣包裹还未被送到分拣窗格的情况，则将任务分割为两段，第一段规划到分拣窗格，第二段规划到出口；

43、情况2：单次路径规划方法无法根据无冲突路径长度进行部分路径规划，但可以规划连续的多个目标：

44、针对该情况，构建临时目标点选择策略，并基于临时目标点进行路径规划；

45、情况3：单次路径规划方法无法根据无冲突路径长度进行部分路径规划，并且不能够规划连续的多个目标：

46、针对该情况，与情况2相同，基于临时目标点选择策略进行路径规划，但仅设置一个临时目标点。

47、所述临时目标点选择策略，具体为：

48、选择位于起点和目标点之间的矩形范围内，与起点距离为l的点中选择不与分拣窗格重合并且未被其他agv设为临时目标点的位置作为此agv的临时目标点，临时目标点的候选点集合为：

49、

50、其中，表示所有的候选点，表示地图中位于当前位置和下一个目标点之间的矩形区域中的点的集合，表示在地图中与当前位置距离为l的点的集合，表示地图中的障碍位置，表示已经分配给其他任务做为临时目标点的点的集合。

51、所述情况2，具体为：

52、a)当agv未将分拣包裹运送至分拣窗格，且从当前位置到下一个目标点的距离小于无冲突路径长度时，在当前位置和分拣窗格之间采用临时目标点选择策略，选择合适的位置作为临时目标点；

53、b)当agv未将分拣包裹运送至分拣窗格，且从当前位置到下一个目标点的距离超过无冲突路径长度时，将分拣窗格相邻的位置作为第一个临时目标点，并从无冲突路径长度中减去当前位置与第一个临时目标点的距离后剩下的长度作为从第一个临时目标点到第二个临时目标点的距离，根据此距离，采用临时目标点选择策略，在第一个临时目标点和分拣区域出口之间选择合适的位置作为第二个临时目标点；

54、c)当agv已将分拣包裹运送至分拣窗格，但从当前位置到下一个目标点的距离小于无冲突路径长度时，采用临时目标点选择策略，在当前位置和分拣区域出口之间的矩形区域内随机选择符合要求的位置作为临时目标点；

55、d)当agv已将分拣包裹运送至分拣窗格，且从当前位置到下一个目标点的距离超过无冲突路径长度时，直接将为此任务规划的分拣区域出口设置为临时目标点。

56、本发明具有以下有益效果及优点：

57、1.本发明方法针对大规模动态agv路径规划问题中重规划周期对agv数量和路径最优性存在影响的特点，采用数据拟合的方法得到三者之间的关系，然后进一步结合任务完成速率的分析，得到重规划周期在整体上对任务完成速率的影响关系。通过此关系可以在系统运行前选取最合适的重规划周期，以最大化任务完成速率。这样可以在整体上减少系统因为超时计算所造成的等待，提升系统的效率。

58、2.本发明方法针对大规模动态agv路径规划问题中无冲突路径长度对求解时间存在影响的特点，采用数据拟合的方法得到二者之间的关系，然后进一步结合重规划周期选择最长的无冲突路径长度。通过此方法可以保证在单次规划的时间限制内尽可能的优化路径，从而缩短最终规划所得路径的长度，降低运输成本，提升分拣效率。

59、3.本发明方法针对分拣系统网格拓扑地图的特点，采用基于矩形区域的临时目标点选择方法，解决了部分单次路径规划方法无法根据无冲突路径长度直接进行路径规划的问题，提升了整个方法的通用性。通过此方法，可以让多种单次路径规划方法都可以被应用于所提出的方法中，从而根据不同的任务需求选择最合适的单次路径规划方法。