量子随机预言机模型下基于格的两轮n-out-of-n门限签名生成方法

本发明涉及信息安全，尤其涉及量子随机预言机模型下基于格的两轮n-out-of-n门限签名生成方法。

背景技术：

1、由于数字签名本身具备不可否认性和公开可验证性等基本属性，因此常用数字签名来确保信息的正确性和真实性。数字签名方案为信息的安全传递和接收提供了更强的安全保障。数字签名的一切都建立在签名私钥安全的基础之上，一旦私钥泄露，攻击者将很容易完成身份的伪造以及非授权访问等恶意行为。在传统的数字签名方案中，签名的私钥是由单一主体掌握，通常通过加密存储或者通过硬件保护等方式进行存储，但是仍然具备极大的使用风险。攻击者可以通过网络攻击的方式入侵签名者计算机，即使加密存储，也能够在签名过程中在内存中抓取私钥，从而窃取签名密钥；无论是硬件还是软件存储的方式，都存在单一节点失效风险。

2、分布式签名是由多个签名参与方共同生成签名的过程，签名所使用的密钥不再由单一方掌握和控制，这正是解决数字签名私钥中心化控制安全性风险的方案。尽管分布式签名协议已经被研究了很长时间，但近年来，由于区块链等主题的新应用，分布式签名协议重新引起了人们的兴趣。然而，大部分分布式签名协议都是基于离散对数假设或大整数分解假设，这些方案并不能抵抗量子攻击。基于格的分布式签名协议方案是抗量子门限签名方案中最有前景的候选方案之一。

3、门限签名是分布式签名的一种，其核心思路是私钥不再由单个节点掌握，而是拆分为多个碎片并由多个节点掌握，从而实现私钥的高安全性和可用性。具体而言，门限签名是普通数字签名“门限化”后的结果，它将签名的权力分散到一组节点，只需超过门限值数量的节点合作，即可完成签名的生成。因此可以认为普通数字签名算法的签名过程是“中心化”的，而门限签名算法的签名过程是“分布式”的。

4、由于随机预言机具有更好的效率，我们想要在随机预言机模型下证明门限签名的安全性。目前已经存在基于格的门限签名方案，但是这些基于格的门限签名方案的安全性仅在经典随机预言机模型中得到了证明。在经典随机预言机中，攻击者仅能通过经典询问的方式获得相应的值，而并不能进行量子询问。对于量子计算机，攻击者是以量子叠加态的形式作为输入询问随机预言机的，即一次询问很多个点。由于hash函数可以用量子算法实例化，为了保证方案对量子计算机具有完整的量子安全性，攻击者应该具有对随机预言机使用量子询问的能力，即运行攻击者以叠加态的形式进行询问。

技术实现思路

1、为了解决现有技术中存在的问题，本发明提供量子随机预言机模型下基于格的两轮n-out-of-n门限签名生成方法，并给出了量子随机预言机模型下基于格的两轮n-out-of-n门限签名的实例化构造，本发明的门限签名方案基于量子随机预言机模型和格上的困难假设，在允许敌手对随机预言机进行量子询问的情况下，仍能保证方案的安全性。

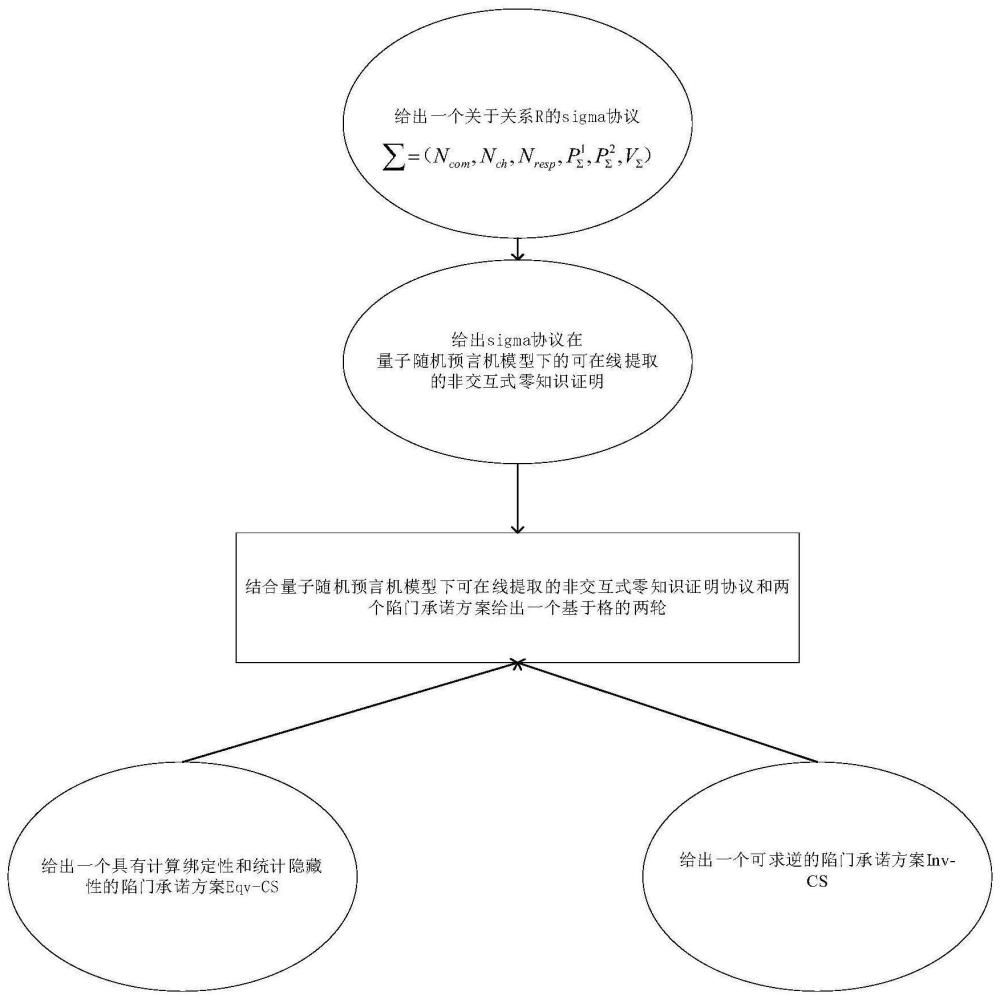
2、为了实现上述目的，本发明采用的技术方案是：量子随机预言机模型下基于格的两轮n-out-of-n门限签名生成方法，结合具有计算绑定性和统计隐藏性的同态陷门承诺方案、可以求逆的同态陷门承诺方案和非交互式零知识证明协议的思想，协议涉及两种类型的角色以及四个算法或子协议；两种类型的角色包括n个联合签名者p1,…pn和验证者，四个算法或子协议包括：setup、genj、signj和verify，包含如下步骤：

3、n个联合签名方共同运行setup算法，生成公共参数pp；为了效率，也可由可信方生成公共参数；

4、pj基于公共参数pp运行门限签名密钥生成协议genj，pj生成自己的私钥份额ski，并根据各自的私钥份额skj，通过与其他联合签名者进行交互共同生成公钥pk；

5、pj基于待签名的消息使用各自的私钥份额skj和公钥pk运行门限签名算法signj，通过与其他联合签名者进行两轮交互共同生成消息的签名；

6、验证者基于各个参与方共同生成的签名和公钥运行门限签名验证算法verify，验证生成签名的有效性。

7、进一步的，获取一个关于关系r的sigma协议ncom,nch,nresp具体包括：

8、s11、证明者以(x,w)∈r为输入，验证者vσ以x为输入；

9、s12、首先证明者生成承诺com：com∈ncom并将com发送给验证者；

10、s13、验证者vσ收到承诺后，生成挑战ch：vσ(x,com)→ch，ch∈nch并将ch发送给证明者；

11、s14、证明者收到挑战后，生成回应resp：resp∈nresp并将resp发送给验证者；

12、s15、验证者收到resp后，验证(com,ch,resp)是否是合法的证据:vσ(x,com,ch,resp)→b；证据合法则，b＝1；否则，b＝0；

13、进一步的，获取基于sigma协议的量子随机预言机模型下的可在线提取的非交互式零知识证明协议π包括：

14、s21、设置安全参数λ，运行nizksetup算法，输出公共参数crs；公共参数定义了有界整数t,m；其中m≤|nch|；

15、s22、以(x,w)和公共参数crs为输入，运行nizkprove算法，其中(x,w)∈r，首先使用所述sigma协议生成t·m个证据(comi,chi,j,respi,j)，其中i∈[t],j∈[m]；然后，使用一个置换函数g对生成的t·m个回答respi,j进行承诺：hi,j＝g(respi,j)，其中i∈[t],j∈[m]；之后，通过随机预言机h获得挑战，即j1||...||jt＝h(x,(comi)i,(chi，j)i,j,(hi,j)i,j)；最后，根据获得的挑战，仅仅公开与挑战位置一致的回应，得到非交互式协议的证明

16、s23、以(x,π)为输入，运行nizkverify算法，其中π＝((comi)i,(chi，j)i,j,(hi,j)i,j,(respi)i)，首先根据(x,π)恢复出挑战，即j1||...||jt＝h(x,(comi)i,(chi，j)i,j,(hi,j)i,j)，然后依次进行以下检查：检查chi,1,...chi,m是否各不相同，其中i∈[t]；检查是否其中i∈[t]；检查是否其中i∈[t]；如果上述检查都通过，则返回1；否则返回0。

17、进一步的，非交互式证明协议满足以下性质：

18、完备性：一个非交互式证明系统(nizksetup，nizkprove，nizkverify)是完备的当且仅当对于任何量子多项式时间预言机算法都有是可忽略的；

19、零知识性：给定一个模拟算法(snizksetup,snizkprove)，预言机s′nizkprove(x,w)执行以下操作：如果返回⊥；否则返回snizkprove(x)；一个非交互式证明系统(nizksetup，nizkprove，nizkverify)是零知识的当且仅当存在一个多项式时间的模拟算法(snizksetup,snizkprove)使得对于任何量子多项式时间预言机算法都有是可忽略的；

20、模拟健壮在线可提取性：对应的模拟者为(snizksetup,snizkprove)的一个非交互式证明系统(nizksetup，nizkprove，nizkverify)是模拟健壮在线可提取的当且仅当存在一个多项式时间的提取者e使得对于任何量子多项式时间预言机算法都有

21、是可忽略的，其中simproofs是snizkprove返回的所有证明的集合。

22、进一步的，所述具有计算绑定性和统计隐藏性的同态陷门承诺方案eqv-cs＝(eqv-csetup,eqv-cgen,eqv-commitck,eqv-openck,eqv-tcgen,eqv-tcommittck,eqv-eqvck)具体如下：

23、eqv-csetup(1λ)→cppeqv:输出公共参数，公共参数定义了集合eqv-sck,eqv-smsg,eqv-sr,eqv-scom,eqv-std和采样随机数的分布d(eqv-sr)；

24、eqv-cgen(cppeqv)→ck：以公共参数做为输入，从承诺密钥空间输出一个密钥ck∈eqv-sck；

25、eqv-commitck(msg；r)→com：以消息空间的一个消息msg∈eqv-smsg和r∈eqv-sr做为输入，输出承诺com∈eqv-scom；

26、eqv-openck(com,r,msg)→b:如果所输入的元组是有效的则输出1，否则输出0；

27、eqv-tcgen(cpp)→(tck,td)：以公共参数做为输入，从承诺密钥空间输出一个密钥tck∈eqv-sck和一个陷门td∈eqv-std；

28、eqv-tcommittck(td)→com：以陷门td做为输入，输出一个承诺com∈eqv-scom；

29、eqvtck(td,com,msg)→r:输出随机数r∈eqv-sr，该r与输入的com,msg使得opentck(com,r,msg)＝1。

30、进一步的，可求逆的同态陷门承诺方案inv-cs＝(inv-csetup,inv-cgen,inv-commitck,inv-openck,inv-tcgen,invck)具体如下：

31、inv-csetup(1λ)→cppinv:输出公共参数，公共参数定义了集合inv-sck,inv-smsg,inv-sr,inv-scom,inv-std和采样随机数的分布d(inv-sr)；

32、inv-cgen(cppinv)→ck：以公共参数做为输入，从承诺密钥空间输出一个密钥ck∈inv-sck；

33、inv-commitck(msg；r)→com：以消息空间的一个消息msg∈inv-smsg和r∈inv-sr做为输入，输出承诺com∈inv-scom；

34、inv-openck(com,r,msg)→b:如果所输入的元组是有效的则输出1，否则输出0；

35、inv-tcgen(cpp)→(tck,td)：以公共参数做为输入，从承诺密钥空间输出一个密钥tck∈inv-sck和一个陷门td∈inv-std；

36、invck(td,com)→msg:以(td,com)为输入，输出com的原像msg。

37、进一步的，具有计算绑定性和统计隐藏性的和可求逆的同态陷门承诺方案满足以下性质：

38、正确性：eqv/inv-cs是正确的如果对于任意的消息msg∈eqv/inv-smsg，

39、

40、绑定性：eqv/inv-cs是绑定的的如果对于任意概率多项式算法以下概率是可忽略的

41、

42、隐藏性:eqv/inv-cs是隐藏的的如果对于任意概率多项式算法以下概率是可忽略的

43、

44、陷门安全性:eqv/inv-cs有安全的陷门如果对于任意消息msg∈eqv/inv-smsg，(ck,msg,com,r)和(tck,msg,com′,r′)的统计距离∈td/∈′td对于安全参数λ是可忽略的，其中

45、

46、

47、均匀密钥性:如果cgen(cpp)的输出遵循密钥空间eqv/inv-sck上的均匀分布，则承诺密钥是均匀的，

48、加法同态性：承诺方案被认为是加法同态的，如果对于任何msg,msg′∈eqv/inv-smsg,

49、

50、进一步的，pn以公共参数pp为输入运行门限签名密钥生成协议genn，pn生成自己的私钥份额skn，并根据各自的私钥份额skn，通过与其他联合签名者进行交互共同生成公钥pk包括：

51、以setup生成的公共参数pp为输入，pn采样私钥份额skn，根据私钥份额skn计算公钥份额pkn，使用随机预言机对对(pkn,n)进行承诺，gn←h1(pkn,n)，gn为(pkn,n)的承诺，将gn发送给其他参与方；

52、pn收到所有其余n-1方发送的gu(u∈[n-1])后，将公钥份额pkn发送给其他参与方；

53、pn收到所有其余n-1方发送的pku(u∈[n-1])后，如果gu≠h1(pku,u)则终止，否则设置组合公钥为pk:＝∑u∈[n]pku；

54、如果协议没有终止，那么第n方pn获得(skn,pk)做为本地输出。

55、进一步的，pn基于待签名的消息使用各自的私钥份额skn和公钥pk运行门限签名算法signn，通过与其他联合签名者进行两轮交互共同生成消息的签名包括：

56、signn算法以序列号sid，密钥对(skn,pk)，待签名的消息μ为输入；获取输入后首先判断序列号sid是否在之前被使用过，如果使用过则不执行协议；

57、pn计算承诺秘钥ck←h3(μ,pk)，ck‘←h4(μ,pk)，ck,ck‘为具有计算绑定性和统计隐藏性的同态陷门承诺方案、可求逆的同态陷门承诺方案eqv-cs、inv-cs的承诺密钥；

58、pn调用nizkprove算法生成t×m个证据；

59、对于每个生成m个挑战；

60、根据生成的挑战和承诺计算回应：

61、将nizkprove中的置换g实例化为具有同态性质的陷门承诺inv-cs，使用对所有的进行承诺：其中(i∈[t],j∈[m])；

62、进行第一轮交互：将发送给其他参与方，收到所有其余n-1方发送的后，计算

63、使用nizkprove的方法获得挑战：

64、将获得的挑战的对应位置的签名公开，即进行第二轮交互：将发送给其他参与方；

65、验证其他联合签名者的签名份额的有效性：收到所有其余n-1方发送的后,对于所有i∈[t]，根据重构comi，然后验证验证验证如果上述验证都成立则对所有i∈[t]计算否则协议中止；

66、如果协议没有终止，第n方pn获得μ的一个签名做为本地输出。

67、进一步的，验证者基于各个参与方共同生成的签名和公钥运行门限签名验证算法verify，验证生成签名的有效性时，验证算法以签名所签名的消息μ，公钥pk做为输入，结合nizkverify(pk,(μ,σ,ci,j))算法的思想进行验证：

68、首先计算承诺密钥ck←h3(μ,pk)，ck‘←h4(μ,pk)，获取挑战ci,j＝h0(i,j,μ,pk,ck,ck‘)并计算

69、然后进行以下几个验证①验证对于相同的i,u，ci，1,...ci，m是否各不相同；②通过重构comi，然后验证③验证上述四个验证全部成功则验证通过，验证算法输出1；否则，验证不通过，验证算法输出0。

70、与现有技术相比，本发明至少具有以下有益效果：本发明采用以上技术方案，给出了一个量子随机预言机模型下基于格的两轮n-out-of-n门限签名生成方法，并给出了量子随机预言机模型下基于格的两轮n-out-of-n门限签名的实例化构造，本发明的门限签名方案基于量子随机预言机模型和格上的困难假设，在允许敌手对随机预言机进行量子询问的情况下，仍能保证方案的安全性。本发明所述门限签名方案在签名阶段只需要签名方之间进行两轮交互，具有低轮次复杂性，减少了通信次数，提升了通信效率；进一步的，由于在我们的方案中各个签名参与方在本地进行拒绝抽样，因此克服了由于参与者数量的增加而导致的各方效率下降的问题。