一种基于焓值法的固液相变数值模拟效率优化方法

本发明属于固液相变问题的数值求解，具体涉及一种基于焓值法的固液相变数值模拟效率优化方法。

背景技术：

1、目前，相变储能技术在太阳能等可再生能源的存储和释放、工业余热的回收以及特殊合金的制备等领域具有巨大的应用潜力，是目前储能领域的研究热点。固液相变具有相变过程体积变化小、温度连续稳定、储能密度大、经济性高及物性稳定等优势，是目前相变储能技术的主要选择。然而，大多数固液相变过程中涉及到的对流影响并不容忽视。因此，进一步理解整个固液相变的过程以及含对流的固液相变过程中的流动和传热机制对于提高相变储能过程的效率至关重要。尤其是含对流的固液相变问题本身属于强非线性问题，通常无法从理论上精确求解，而实验研究往往需要耗费更大的资源和成本。因此，先通过数值模拟给出较为可靠的结果后通过实验进行互相验证是一种合适的选择。

2、近几十年随着计算机硬件的发展，计算机性能大幅提升，这促进了诸多应用于相变问题的数值方法，例如焓值法(又称焓-多孔介质方法)、格子玻尔兹曼方法(latticeboltzmann method,lbm)及相场法等。焓值法因其物理意义明确、实现方便，是目前应用最广泛的方法之一。该方法通过引入焓，将其与温度一起作为能量方程的待求函数，进而在整个计算域内建立了形式统一的能量方程。该方法无需要追踪相界面的具体位置，并且通常会利用多孔介质的概念处理固液相之间的糊状区域。

3、近年来，在经典的焓值法的基础上，研究人员又发展出了各种各样的改进焓值法。然而，大多数计算过程仍然基于预测-校准策略，例如求解非稳态计算时常用的simple、piso等类似算法。由于固液相变储能中采用的相变材料往往具有非常大或非常小的普朗特数(pr)，这对时间步长的要求很高、且每一时间步都需要大量的迭代，这可能导致计算时间过长、计算结果不够准确、计算资源浪费等问题。因此，对于基于焓值法的固液相变问题的计算，亟需开发一种新的优化算法以提高计算效率和准确性。

技术实现思路

1、本发明的目的在于是针对现有基于焓值法计算所存在的问题，并提供一种基于焓值法的固液相变数值模拟效率优化方法。该方法采用双时间步计算，通过交错网格和谱方法求解压力泊松方程避免产生迭代误差，在保证求解准确度的前提下，大幅提升了固液相变问题的计算效率。

2、本发明所采用的具体技术方案如下：

3、本发明提供一种基于焓值法的固液相变数值模拟效率优化方法，具体步骤如下：

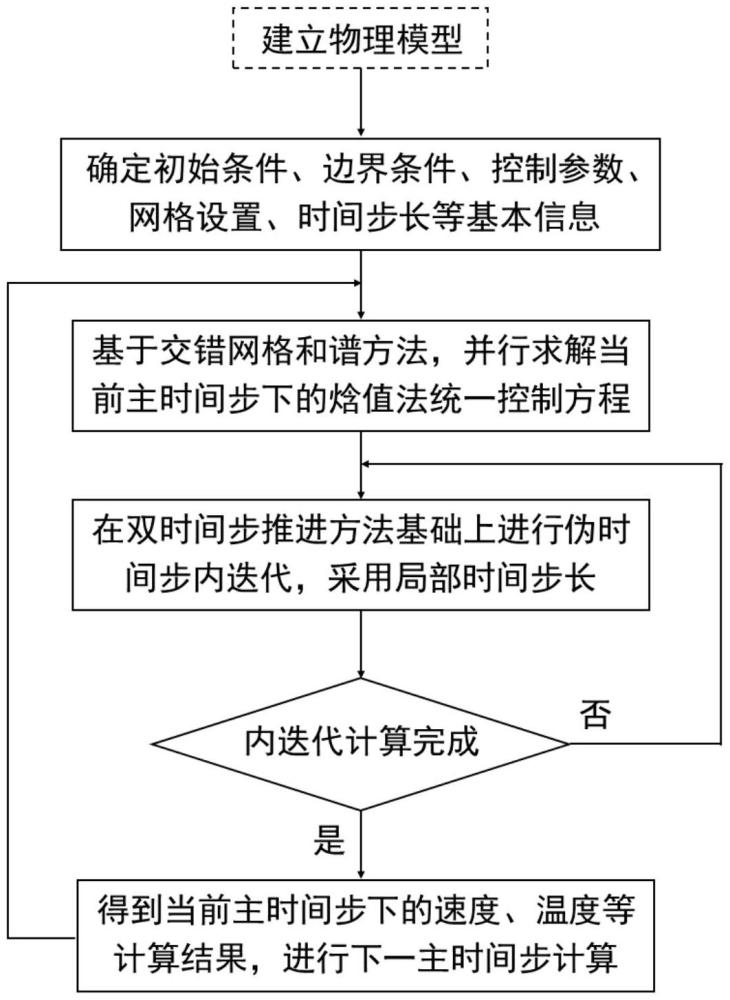
4、s1：根据待模拟的固液相变过程建立对应的物理模型，对数值模拟计算区域网格划分和并行区域划分；

5、s2：设置数值模拟计算所需的初始条件、边界条件、控制参数、主时间步和伪时间步；

6、s3：根据相变材料的普朗特数pr的大小选取不同计算参数各自推进的时间步长：若pr≤1时，将速度按照主时间步进行推进，温度按照伪时间步进行推进；若pr＞1时，将温度按照主时间步进行推进，速度按照伪时间步进行推进；

7、s4：针对每一个并行区域，基于由连续性方程、动量方程和能量方程组成的统一控制方程，在有限差分法的基础上进行空间离散，并使用双时间步推进方法，在当前主时间步内对主时间步对应的参数进行求解计算，再在每个主时间步内采用伪时间步进行内迭代，求解伪时间步对应的参数，直至该内迭代完成预设次数，最终得到当前主时间步下所有待求解参数的计算结果；其中，在每个主时间步的计算中，动量方程内的压力通过采用谱方法中的离散余弦变化进行压力投影法，并结合交错网格求解压力泊松方程得到；所有并行区域完成每个主时间步的并行计算后，将各并行区域的模拟结果进行通信交互；

8、s5：迭代重复步骤s4，进行下一主时间步的计算，直至完成预设主时间步数，得到最终的计算结果；所述计算结果包括数值模拟计算区域内的速度场、压力场、温度场和液相分数场。

9、作为优选，步骤s1中所述物理模型采用固液相变模型。

10、作为优选，所述并行区域划分后，在实际计算过程中需在各方向的并行区域边界增加1层虚拟边界，以满足差分要求和相邻区域的通信。

11、作为优选，所述控制参数为由边界条件和相变材料参数决定的无量纲参数，包括瑞利数ra、普朗特数pr和斯蒂芬数ste。

12、作为优选，所述统一控制方程中的连续性方程、动量方程和能量方程的无量纲形式分别为：

13、

14、式中：u、p、θ、f为统一控制方程中的四个待求解参数，其中u为速度矢量，p为压力，f为局部液相分数，θ为局部温度；为哈密顿算子，t为时间，j为重力方向上的单位矢量；a为无量纲糊状区常数，ε为防止分母为0的无限小计算常数；δθm为无量纲相变温度区间，δθm＝θl-θs，其中θl为使相变材料的局部液相分数为1的最低温度，θs为使相变材料的局部液相分数为0的最高温度；

15、所述能量方程中引入赫维赛德函数，计算方法如下：

16、

17、式中：θm为相变材料的融化温度，中间参数σ＝δθm/2-|θ-θm|。

18、作为优选，所述空间离散采用二阶有限差分格式。

19、作为优选，步骤s4中主时间步和伪时间步的推进计算均采用二阶adams-bashforth格式。

20、作为优选，步骤s4中，采用谱方法中的离散余弦变化进行压力投影法，并结合交错网格求解压力泊松方程具体如下：将速度分量存于对应方向上网格边界中心，温度和压力存于网格中心点的交错网格设置，在满足不穿透条件的基础上，利用离散余弦变换求解压力泊松方程得到满足边界条件的压力场，最后通过压力梯度得到精确无散的速度场。

21、本发明相对于现有技术而言，具有以下有益效果：

22、(1)本发明建立的统一控制方程中，通过引入赫维赛德函数，将经典焓值法推导的能量方程中的潜热源项与原有的显热项合并处理。这样无需额外迭代求解潜热源项的步骤，简化了计算步骤，在确保结果准确度的同时提高了计算效率。

23、(2)为了避免求解压力泊松方程时传统算法带来的迭代误差，本发明采用谱方法中的离散余弦变化结合交错网络进行压力投影法，使得压力求解过程无需迭代，且几乎精确满足无散条件，大幅度地缩短了计算时间，同时也保证了结果的准确性。

24、(3)本发明基于更常见的储能材料性能，采用了双时间步长方法，基于普朗特数pr调整主时间步长和伪时间步长，保证结果准确度的同时大幅提升计算效率，减少计算资源消耗。

技术特征：

1.一种基于焓值法的固液相变数值模拟效率优化方法，其特征在于，具体步骤如下：

2.根据权利要求1所述的基于焓值法的固液相变数值模拟效率优化方法，其特征在于，步骤s1中所述物理模型采用固液相变模型。

3.根据权利要求1所述的基于焓值法的固液相变数值模拟效率优化方法，其特征在于，所述并行区域划分后，在实际计算过程中需在各方向的并行区域边界增加1层虚拟边界，以满足差分要求和相邻区域的通信。

4.根据权利要求1所述的基于焓值法的固液相变数值模拟效率优化方法，其特征在于，所述控制参数为由边界条件和相变材料参数决定的无量纲参数，包括瑞利数ra、普朗特数pr和斯蒂芬数ste。

5.根据权利要求1所述的基于焓值法的固液相变数值模拟效率优化方法，其特征在于，所述统一控制方程中的连续性方程、动量方程和能量方程的无量纲形式分别为：

6.根据权利要求1所述的基于焓值法的固液相变数值模拟效率优化方法，其特征在于，所述空间离散采用二阶有限差分格式。

7.根据权利要求1所述的基于焓值法的固液相变数值模拟效率优化方法，其特征在于，步骤s4中主时间步和伪时间步的推进计算均采用二阶adams-bashforth格式。

8.根据权利要求1所述的基于焓值法的固液相变数值模拟效率优化方法，其特征在于，步骤s4中，采用谱方法中的离散余弦变化进行压力投影法，并结合交错网格求解压力泊松方程具体如下：将速度分量存于对应方向上网格边界中心，温度和压力存于网格中心点的交错网格设置，在满足不穿透条件的基础上，利用离散余弦变换求解压力泊松方程得到满足边界条件的压力场，最后通过压力梯度得到精确无散的速度场。

技术总结本发明公开了一种基于焓值法的固液相变数值模拟效率优化方法，步骤如下：建立物理模型，进行网格划分和并行区域划分；设置计算所需的条件；根据Pr的大小选取不同计算参数各自推进的时间步长；针对每一个并行区域，基于统一控制方程，进行空间离散，并使用双时间步推进方法，对主时间步对应的参数进行求解，再采用伪时间步进行内迭代求解，直至该内迭代完成，得到当前主时间步下的计算结果；各并行区域的模拟结果进行通信交互；在每个主时间步的计算中，动量方程内的压力通过采用谱方法中的离散余弦变化进行压力投影法，并结合交错网格求解得到；重复上述步骤进行下一主时间步的计算。该方法确保固液相变问题计算结果准确度的同时提高计算效率。技术研发人员：夏振华,胡瑾受保护的技术使用者：浙江大学技术研发日：技术公布日：2024/8/20