一种电缆终端塔三维引线布置及间隙校验的方法与流程

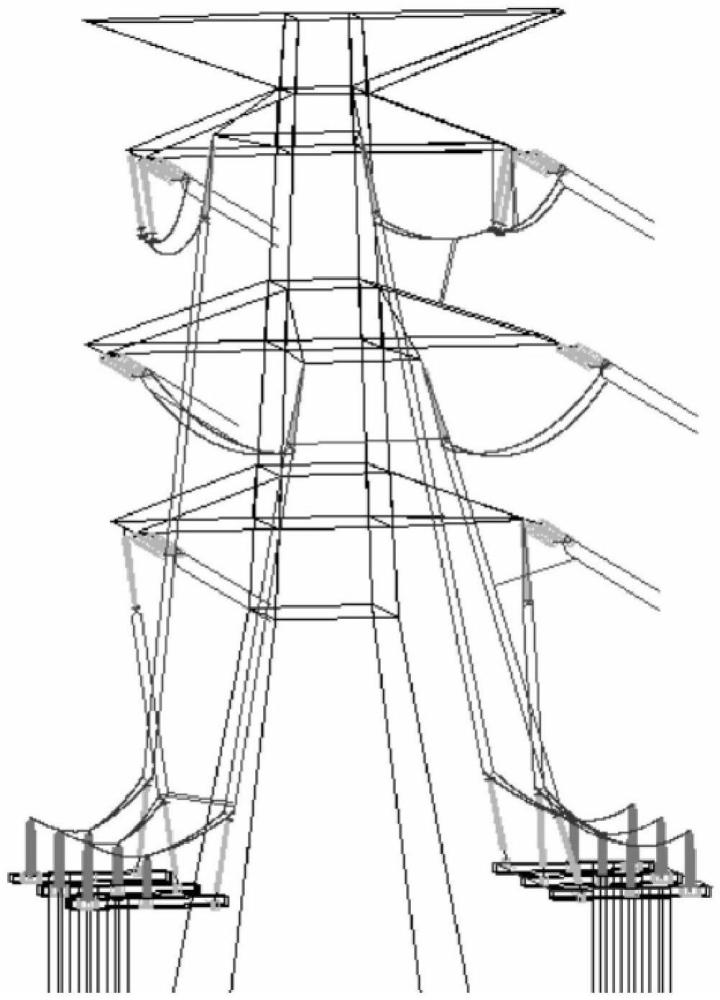
本发明涉及一种电缆终端塔三维引线布置及间隙校验的方法，属于电缆终端三维布置及间隙计算。

背景技术：

1、目前，电缆终端塔优化布置均在cad二维环境中进行，间隙计算采用人工投影法，在cad中量取并计算，计算精度不高，计算速度较慢。

技术实现思路

1、为提高电缆终端塔优化布置效率，提高间隙计算精度，本发明提供一种电缆终端塔三维引线布置及间隙校验的方法。

2、第一方面，本技术提供一种电缆终端塔三维参数化建模方法；包括以下步骤：

3、针对杆塔，建立空间直角坐标系，具体包括：以杆塔地面中心为坐标原点，以横担方向为x轴，以线路方向为y轴，以垂直地面方向为z轴，建立空间直角坐标系；

4、通过杆塔根开、边坡位置高度、呼高、层高、横担长、横担端部宽度、杆塔主材顶部宽度参数，输入建立杆塔模型；

5、通过电缆平台高度、相间宽度、引线串位置、避雷器位置、电缆终端头位置参数，输入建立电缆平台模型；

6、通过塔身引线串挂点位置距离塔身的距离，输入建立引线横担挂点位置，通过三维绘制引线横担杆件，建立引线横担模型；

7、通过绝缘子串低压侧长度、联间距、绝缘子长度、高压侧长度、分裂间距、均压环位置及尺寸参数，输入建立绝缘子串模型；模型建成后，耐张串以杆塔挂点为基点，通过输入在xy平面内旋转角度和在垂直xy平面方向旋转角度确定空间位置；跳线串以杆塔挂点为基点，通过输入沿横担方向偏角度数确定空间位置；引线串以引线横担挂点为基点，通过点选引线两端挂点确定引线方向；

8、通过连接上下引线串建立上下引线串之间的引线模型，通过两点+弧垂方式建立跳线及电缆终端头位置处的引线模型。

9、第二方面，本技术提供一种电缆终端塔相间和相对地最小水平距离的计算方法。包括以下步骤：

10、通过参数化建模，将带电部分和接地部分三维模型简化为空间点、空间线段和空间平面，因此相间和相对地最小水平距离数学模型为空间点、空间线段和空间平面之间的最小距离。

11、(1)空间点到空间线段最小距离计算：

12、线段不同于直线是无限延伸的，所以点到线段的距离需要考虑线段的两端，如图1所示，有以下三种情况：a.点到线段的垂直投影点在线段上,最小距离为pd；b.点到线段的垂直投影点在线段左边延长线上，最小距离为ap；c.点到线段的垂直投影点在线段右边延长线上,最小距离为bp；即灰色箭头所表示的线段即为最短距离所处的线段。

13、以上情况均有向量

14、即向量ad＝r·ab

15、设定dot为向量点积函数，mold为求向量模函数,cross为向量叉乘。

16、

17、由图1可知当r<0时最短距离为ap；

18、大于1时最短距离为bp；

19、否则为pd；

20、其中

21、(2)空间中两条线段之间的最短距离:

22、设空间中有两条线段ab和cd，设a点的坐标为(x1,y1,z1)，b点的坐标为(x2,y2,z2)，c点的坐标为(x3,y3,z3)，d点的坐标为(x4,y4,z4)。

23、设p是直线ab上的一点，p点的坐标(x,y,z)可以表示为

24、

25、当参数0≤s≤1时，p是线段ab上的点；当参数s＜0时，p是ba延长线上的点；当参数s＞1时，p是ab延长线上的点。

26、设q是直线cd上的一点，q点的坐标(u,v,w)可以表示为

27、

28、当参数0≤t≤1时，q是线段cd上的点；当参数t＜0时，q是dc延长线上的点；当参数t＞1时，q是cd延长线上的点。

29、p,q两点之间的距离为

30、

31、距离的平方为

32、f(s,t)＝pq2＝(x-u)2+(y-v)2+(z-w)2

33、＝[(x1-x3)+s(x2-x1)-t(x4-x3)]2+[(y1-y3)+s(y2-y1)-t(y4-y3)]2

34、+[(z1-z3)+s(z2-z1)-t(z4-z3)]2。

35、要求直线ab，cd之间的最短距离，也就是要求f(s,t)的最小值。

36、对f(s,t)分别求关于s，t的偏导数，并令偏导数为0：

37、

38、展开并整理后，得到下列方程组：

39、

40、如果从这个方程组求出的参数s，t的值满足0≤s≤1，0≤t≤1，说明p点落在线段ab上，q点落在线段cd上，这时pq的长度

41、

42、就是线段ab与cd的最短距离。

43、如果从方程组求出的参数s，t的值不满足0≤s≤1，0≤t≤1，说明不可能在线段ab内部找到一点p，在线段cd内部找到一点q，使得pq的长度就是线段ab与cd的最短距离。

44、这时，可以分别求a点到线段cd的最短距离、b点到线段cd的最短距离、c点到线段ab的最短距离、d点到线段ab的最短距离。

45、求法参看“空间点到线路距离计算”的计算过程。

46、然后，比较这4个距离的大小，其中最小的一个，就是线段ab到cd的最短距离。

47、(3)空间点到空间平面最小距离计算：

48、如图2所示，给定一个平面ax+by+cz+d＝0和平面外一点p(x0,y0,z0)，过p点做平面的垂线，垂足为p'(x,y,z),则直线pp’与平面的法向量n平行，所以直线pp’的方程为转化为参数方程得

49、x＝x0-at

50、y＝y0-bt

51、z＝z0-ct

52、带入平面方程求出t

53、

54、将t代入直线参数方程，即可得到p’点坐标。

55、若点p在平面上的投影点p’∈有限平面s，则最小距离d＝|pp’|；若则最小距离d＝p到有限平面s的边界的最小距离，既转化为点到线段的计算模型，通过计算p到平面各边界线段距离，得出p到线各线段的最小距离。

56、(4)空间线段到空间平面最小距离计算：

57、空间线段到空间平面最小距离可转化为点到有限面的距离计算，取最小值。将线段从起点开始，按一定间距读取点的坐标，逐个计算点到平面的距离，取最小值即为空间线段到空间平面最小距离，其误差不大于所选取点的间距。

58、通过上述空间点到空间线段最小距离计算、空间中两条线段之间的最短距离计算、空间点到空间平面最小距离计算、空间线段到空间平面最小距离计算，即可准确得出相间和相对地间的最小距离。

59、本发明的有益效果：本发明提供一种电缆终端塔引线三维建模方法和相间、相对地间最小间隙的计算方法，通过三维参数化建模，快速实现电缆终端塔的引线及电缆平台的布置，通过计算空间点到空间线段最小距离、空间中两条线段之间的最短距离、空间点到空间平面最小距离、空间线段到空间平面最小距离，即可精确得出相间和相对地间的最小距离。因此通过本发明的方法，使得电缆终端塔引线布置速度大大加快，电气间隙校验精度大大提高。