一种基于节点相似性和非负矩阵分解的社区检测方法

本发明属于复杂网络领域，涉及一种基于非负矩阵分解和模块度最大化的社区检测方法。

背景技术：

1、现实中的复杂网络通常具有庞大的节点规模和相对稀疏的节点连接，因此网络呈现高维稀疏特性。处理稀疏网络常用的方法是将网络结构信息存为矩阵形式，并利用矩阵分解来挖掘这些网络的隐藏信息，同时压缩数据、概括，保留有用信息，过滤冗余信息。如果复杂网络数据具有非负性，例如在无权网络中用1或0表示节点连接的有无，或在有权网络中，节点间连接的权重值不可能为负数，此时使用非负矩阵分解(non-negative matrixfactorization,nmf)更有优势。因为nmf方法对于社区检测具有先天优势，基于nmf的社区检测算法是目前最受关注的社区检测方法之一，在研究领域备受关注。现有基于nmf的社区检测方法大多直接分解复杂网络的邻接矩阵，即邻接矩阵就是整个模型的输入矩阵，默认为邻接矩阵包含的信息就是整个网络拓扑的所有信息。然而，随着网络的发展，传统的社区检测方法对于网络拓扑一些关键的信息并没有考虑到，例如反映节点之间倾向性以及相似性信息等都十分隐蔽，而邻接矩阵仅是反映了节点之间的连接性；虽然使用先验信息可以增加输入矩阵所含的信息，但是这种方法只适用于个别已知先验信息的网络，对于没有先验信息或先验信息较少网络来说并不适用。随着复杂网络的飞速发展，仍仅使用邻接矩阵中包含的网络拓扑信息，已经不能适应当前复杂网络的发展。

2、针对输入矩阵所含的网络结构信息不丰富这个问题，本发明从其他方面考虑节点相似性，提出一种基于节点相似性和模块度的非负矩阵分解社区检测方法。该方法主要结合社区检测自身的特点，对传统的聚类系数指标进行改进来表征节点相似性，从而丰富社区检测的输入矩阵，然后利用模块度指标作为每一次划分标准，通过不断迭代使得模块度达到最大，进一步提高社区检测的准确率。

技术实现思路

1、本发明要解决的问题是传统的nmf社区检测算法用到的网络拓扑结构过于简单。本发明在传统nmf算法的基础上结合社区检测自身的特点提出一种新的节点相似性指标，实现丰富社区检测的输入矩阵效果；并把模块度评价指标融合到每一次迭代划分当中，每一次迭代都把最大化模块度指标作为迭代目标，反复更新划分结果直到模块度收敛。

2、本发明的技术解决方案是：

3、(1)构建节点相似性指标

4、根据newman提出的社区内部节点的特点：社区内部的节点连接紧密，社区间的节点连接稀疏；以及聚类系数的含义：反应邻居节点间连接的紧密程度；两者在表示连接紧密程度方面不谋而合，提出基于聚类系数的节点相似性指标。首先，聚类系数的描述如下：给定一个节点k，它的度为ki，这个邻居之间最多能够产生条链接，则节点的局部聚类系数(local clustering coefiicient)定义为此节点邻居之间链接的数目与邻居之间最大可能产生的链接数目之比：

5、

6、li代表节点的邻居之间实际存在的连接数。通过对聚类系数的深入研究发现：li可以看作是包含节点i的三角形数目，而包含节点j的连通三元组(包含节点i的3个节点，且至少有两条边经过节点i到达剩余两个节点数目最大为包含节点i的3个节点，且至少有两条边经过节点i到达剩余两个节点)数目最大为因此局部聚类系数的另外一种定义为：

7、

8、可以看出ci越高代表节点i周围的邻居连接越紧密。

9、由上面的分析可以看出，聚类系数是研究某一个节点的邻居节点间连接的紧密程度。对于我们想要的节点相似性，应该是探究两个节点间的相似性，参考前面聚系数的第二种定义，我们尝试提出用于两个节点的节点相似性指标：

10、对于复杂网络中的两个节点i，j，它们各自的邻居节点集合分别记为ui以及uj，若ui中的某一个节点和uj中的某一个节点存在一条实际的连接，则，变量加1；此时，若先假设节点i和j是可达的，此时这条实际的链接与节点i，j就可以构成一个四边形；其中能够组成最大四边形的数量为|ui|*|uj|，考虑ui和uj中间可能是存在共同邻居的，因此设定变量f的初始量为ui和uj中的共同邻居数量，若i和j是可达的，变量f额外加1。至此我们提出的基于聚类系数的节点相似性指标的公式为：

11、

12、其中f的赋值规则如下：

13、

14、将前面提出的基于聚类系数的节点相似性指标结果构成一个相似矩阵k；

15、92)构建最大化模块度约束条件

16、采用基于模块化最大化的社区检测方法如下：

17、模块度是揭示网络在进行社区划分后与随机网络(无社区结构)的差别，这种差别越大，说明社区检测的结果越好。模块度的定义如下：

18、

19、对于两个社区的情况，即k＝2时。若ci＝1代表第i个节点属于正类，反之ci＝-1则代表该节点属于负类。矩阵c即为社区指示矩阵。进一步，(5)式可以重写为矩阵形式：

20、

21、其中b为模块度矩阵：

22、

23、拓展到多个社区(k＞2)，社区指示矩阵变为c∈rn×k，其中每一列代表一个社团，对于非重叠社区，该矩阵每行中仅有一个元素为1，其余元素均为0，因此有tr(ctc)＝n。进一步，(6)式可写作：

24、q＝tr(ctbc)  (8)

25、(3)构建相似性约束条件

26、为使得在原有几何空间中接近的节点，在通过nmf得到的基向量的表示也彼此接近(也叫局部不变假设)，所以考虑通过拉普拉斯矩阵构建相似度的约束条件。拉普拉斯矩阵(laplacianmatrix)在图论中应用广泛，又名导纳矩阵，本质是用矩阵的形式表示某个图。给定图g＝(v，e)，它的拉普拉斯矩阵被定义为l＝d-k，其中d为图的度矩阵，因为相似的节点更可能被划分到同一社区中，因此基于正则化的节点相似度矩阵可以表示为下列公式：

27、

28、ci，cj代表节点i，j所属的社区，将上式推广到矩阵可得如下表示：

29、

30、其中，l即为拉普拉斯矩阵。

31、(4)构建算法的目标函数

32、为了丰富输入矩阵(邻接矩阵a)，我们定义下面的公式：

33、s＝a+ηk(11)η代表相似矩阵所占的权重，因此非负矩阵分解的公式为：

34、s≈uv(u≥0，v≥0)    (12)

35、传统的nmf社区检测方法的目标函数为：

36、

37、考虑了相似性约束条件和最大化模块度约束条件后，可以得到算法的目标函数为：

38、

39、目标函数中的参数α和β均为正数，社区指示矩阵c同时也受相似矩阵的约束，因此包含了更多的网络结构信息。

40、(5)优化目标函数

41、由于该目标函数是非凸的，因此采用迭代更新算法，分别更新u，v，c；更新过程如下所示：

42、更新u，v时，优化函数分别为：

43、

44、固定c，v不变，对u求偏导可得如下结果：

45、l′(u)＝2uvtv-2sv  (17)

46、因此乘法更新规则为：

47、

48、同理，固定c，u不变对v求偏导，然后根据更新乘法规则可得更新规则为：

49、

50、更新c时，固定u，v不变，由于约束条件tr(ctc)＝n，因此优化问题变为：

51、

52、其中要求解(20)式是一个np-hard问题，因此我们放宽约束：ctc＝i，并为这个新约束引入正则化系数λ，(20)式可以重写为以下形式：

53、

54、λ＞0并且应该足够大，以确保满足正交性。优化过程中再引入拉格朗日乘子矩阵θ，因此重写式子(21)：

55、

56、对(22)求导并令之等于0可得：

57、θ＝2αdc-2αsc-2βac+2βb1c+4λcctc-4λc    (23)

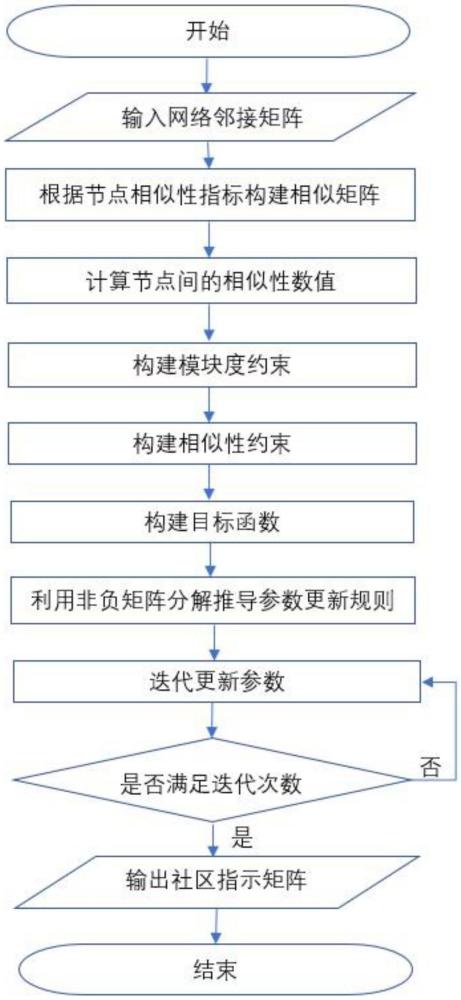
58、对非负矩阵c满足karush-kuhn-tucker(kkt)条件，可以得到方程(24)：

59、(2αdc-2αsc-2βac+2βb1c+4λcctc-4λc)ijcij＝θijcij＝0，

60、(24)

61、给定初始矩阵c，最终得到满足kkt条件的非负社区指示矩阵c的更新规则：

62、

63、其中，

64、

65、利用以上的更新规则，可以得到本算法的优化过程，具体见下述表1中的算法。在算法1的更新矩阵过程中，更新一个矩阵时，固定另一个矩阵不变；迭代过程的终止条件为矩阵收敛或达到给定的迭代次数阈值。

66、下面给出本发明提出的聚类非负矩阵分解(clustering non-negative matrixfactorization，cnmf)社区检测算法流程

67、表1社区检测算法cnmf

68、