基于酉变换实值块稀疏贝叶斯学习的阵列信号处理方法

：本发明涉及雷达信号处理，具体的说是一种能够显著提高参数估计性能的基于酉变换实值块稀疏贝叶斯学习的阵列信号处理方法。

背景技术

0、背景技术：

1、阵列信号处理是现代信号处理的一个重要分支，在近几十年来得到了迅猛发展。与传统阵列相比，极化敏感阵列可以获取信号的空间信息的同时也可以获得电磁信号的极化信息，这使得其在理论上具有明显的优势，具有很好的军事和民用前景。相干源场景在实际中较为常见，如多径效应、电子干扰等场景，而相干源条件下许多经典的参数估计算法失效，因此相干源条件下的参数估计问题是另一大挑战。

2、现有技术中，ong l t提出的空间平滑技术是一种有效的解相干算法，但它是通过牺牲有效阵元数来换取的，对阵列孔径有一定的损失，且在低信噪比时算法性能较差；同时为保证子阵结构相同，需限定阵列阵型为均匀线阵。jian l将空间平滑技术扩展到极化域得到了极化平滑技术，有效实现了相干源的doa估计，且突破了空间平滑技术对阵型的限制，但是，该类算法解相干信号个数有限，解相干信号数为阵元极化方式个数，且在平滑过程中模糊了信号的极化参数，使得不能实现对相干信号极化参数的估计。将空间平滑技术和极化平滑技术结合起来可以实现解相干个数的翻倍，但该类算法仍受阵型限制，且不能估计极化参数。子空间拟合的概念是20世纪90年代之后提出的，其基本思想在于构造这样一个事实：即阵列流型矩阵与阵列接收数据的子空间之间存在一个拟合关系。该类算法不会造成阵列孔径损失，并且适合任意不存在流形模糊的阵型。同时，针对于极化doa估计，学者提出了广义最大似然算法及广义子空间拟合算法，该类算法实现了doa和极化参数的解耦合，降低了搜索的维度，但其仍需要多维搜索，因而存在计算量大的问题。且其在小快拍情况下性能会下降。稀疏重构理论研究最早源于1986年santosa等人提出稀疏信号等概念，可表述为：在给定完备矩阵下，可以用少数非零系数较为完整地表征原始信号。基于稀疏表示的doa估计方法在小快拍情况下性能优越，并且具有天然的解相干能力，在阵列参数估计中得到了广泛的应用。许彬等人将块正交匹配追踪(block orthogonal matchingpursuit,bomp)算法应用于l型极化敏感阵列，实现了doa和极化参数估计，但由于bomp算法原子块无修正能力，参数估计性能较差；张智林提出了经典的块稀疏贝叶斯学习(blocksparse bayesian learning,bsbl)算法，性能优于bomp算法；li b b等人利用期望最大化bsbl(bsbl-expectation maximization,bsbl-em)算法实现了一维情况下的极化敏感阵列的极化和doa参数联合估计，但是经典的块稀疏贝叶斯学习算法只适用于实数，现有技术并未给出具体的实值化方法。

技术实现思路

0、技术实现要素：

1、本发明针对现有技术中存在的缺点和不足，提出了一种能够显著提高参数估计性能的基于酉变换实值块稀疏贝叶斯学习的阵列信号处理方法。

2、本发明通过以下措施达到：

3、一种基于酉变换实值块稀疏贝叶斯学习的阵列信号处理方法，其特征在于，包括以下步骤：

4、步骤1：针对于双正交偶极子阵列，分别构造水平极化子阵和垂直极化子阵；

5、步骤2：分别对两个子阵的接收数据进行酉变换，将接收数据转换为实值数据，同时将doa和极化参数解耦合，进而使用块稀疏算法进行估计；

6、步骤3：利用酉变换的特性，将重构后的块信号进行转换，进而利用块信号之间的相关性实现极化参数的估计。

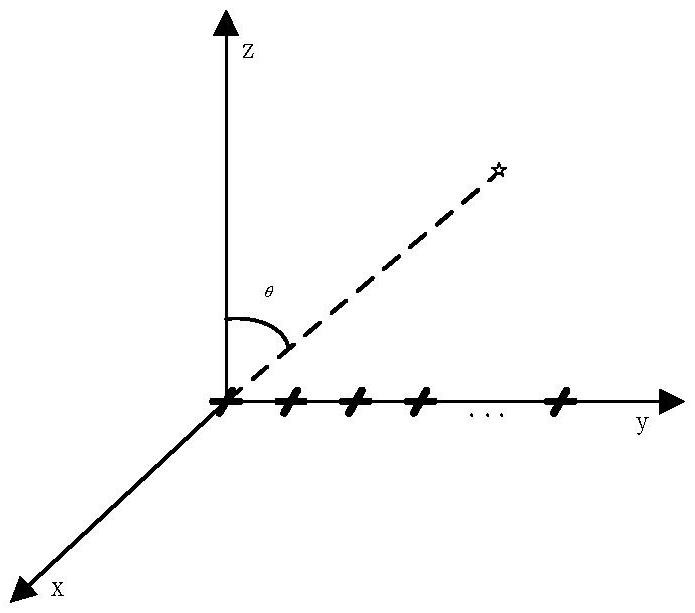
7、本发明在均匀线阵的模型下进行，线阵的可分辨空间域的角度为[-90°，90°]，考虑由空间距为半波长d＝λ/2的m个正交偶极子阵元组成的均匀线阵和p个远场窄带完全极化信号，第p个信号的方位角为θp，极化辅助角和极化相位角分别为γp和ηp，假设入射信号互不相关且与噪声之间相互独立，则该极化敏感阵列的接收信号可以表示为：

8、y(t)＝as(t)+n(t)(1)，

9、其中，是阵列信号的空间极化域联合阵列流形矩阵，s(t)＝[s1(t),s2(t),…,sp(t)]t∈cp×1为p个相互独立的入射信源，n(t)＝[n1(t),n2(t),…,n2m(t)]t∈c2m×1为零均值，方差为σ2的加性高斯白噪声，且对应于第p个信号的理想导向矢量具体表示为：

10、

11、其中，为第p个信号的空域导向矢量；为第p个信号的极化矢量；表示克罗内克积。

12、本发明步骤1中，对于双正交偶极子阵列，分别选取水平极化阵元和垂直极化阵元构造子阵1和子阵2；其中，对于子阵1，有：

13、

14、其中，a(θ)＝[1,exp(-j2πdsin(θ)/λ),…,exp(-j2π(m-1)dsin(θ)/λ)]t,

15、

16、则子阵1接收数据可以表示为

17、

18、其中，e＝diag(e1,e2,…,ep)，a1(θ)＝a(θ)·v1，

19、a(θ)＝[a(θ1),a(θ2),…,a(θp)]，v1＝diag(v1,x,v2,x,…,vp,x)，

20、同理可得，对于子阵2有

21、y2＝a2(θ)e·x+n2(8)，

22、其中，a2(θ)＝a(θ)·v2，

23、v2＝diag(v1,y,v2,y,…,vp,y)；

24、构造增广矩阵：

25、yaug1＝[y1,jmy1*jl] (9)，

26、yaug2＝[y2,jmy2*jl] (10)，

27、其中，jm∈rm，jl∈rl为副对角线上元素均为1，其余元素均为0的置换矩阵。

28、本发明步骤2中所述分别对两个子阵的接收数据进行酉变换，将接收数据转换为实值数据，同时将doa和极化参数解耦合，具体包括：

29、对于子阵1，有：

30、yaug1＝[y1,jmy1*jl]

31、＝[a1ex+n1 jm(a1ex+n1)*jl]

32、＝[a1ex+n1 jma1*e*x*jl+jmn1*jl]

33、＝[a1ex jma1*e*x*jl]+[n1 jmn1*jl] (11)，

34、对于均匀线阵，空域导向矢量存在以下关系：

35、a1λ＝jma1* (12)，

36、其中，

37、λ＝diag{exp(j2π(m-1)sin(θ1)/λ),…,exp(j2π(sin(θp)/λ),1}

38、对增广矩阵进行酉变换，有

39、yr1＝umhyaug1u2l (13)，

40、代入式有

41、yr1＝umh[a1ex jma1*e*x*jl]u2l+umh[n1 jmn1*jl]u2l (14)，

42、对于信号部分有

43、umh[a1ex jma1*e*x*jl]u2l＝umh[a1ex a1λe*x*jl]u2l

44、＝umha1[exλe*x*jl]u2l (15)，

45、令aa1＝umha1，s＝[exλe*x*jl]u2l

46、则有：yr1＝aa1·s+nr1(16)，

47、同理可得，对于子阵2有

48、yr2＝aa2·s+nr2 (17)，

49、构造矩阵

50、

51、本发明均在均匀线阵的模型下进行，线阵的可分辨空间域的角度为[-90°，90°]，设划分成n个网格，可得到一个超完备的角度集合其中，空心圆圈代表划分的网格，实心的圆圈代表信号的来波方向，可以得到超完备角度集合中各个元素对应的阵列导向矢量所构成的矩阵，即为扩展后的阵列流形矩阵，因此将式(18)扩展到超完备角度集合得到超完备阵列输出模型：

52、其中，

53、φ＝[umha1,1,…,umha1,n；umha2,1,…,umha2,n]，sn,n∈[1,n]

54、为块信号。

55、本发明步骤2中，为了将bsbl框架应用于多测量矢量模型，应该将mmv

56、模型转换为单个测量矢量模型：

57、yy＝dd·xx+nn (20)，

58、其中，yy＝vec(yrt)∈c4ml×1,

59、nn＝vec(nrt)∈c4ml×1，vec(·)表示向量化。那么，xx的分块结构表示为：

60、xx＝[x(1:4l)t,x(4l+1:8l)t,…,x(4l(i-1)+1:4li)t,…,x(4l(n-1)+1:4ln)t]t，i＝1,2,…,n，x(4l(i-1)+1:4li)表示由xx的4l(i-1)+1到4li元素组成的4l×1向量，需要注意的是xx是块稀疏的，每个非零块包含4l个元素，因此可采用块稀疏贝叶斯算法进行参数的估计；

61、本发明步骤2中，bsbl算法架构假定第i个信号块服从高斯分布

62、

63、γi控制信号稀疏性，bi描述了块内相关性信息。γi为0代表对应的信号块为0，γi越大，取值的概率越大。假定信号块与块之间是不相关的，则信号可以被建模为

64、其中，γ＝diag-1(γ1b1,…,γgbg)，

65、假定观测噪声独立同分布，即服从均值为0，方差为βi的高斯分布，则的后验分布服从如下的高斯分布：

66、

67、其中，

68、σ-1＝γ-1+φtβφ (24)，

69、μ＝σφtβy(25)，为了估计参量{γi,bi}与β，可采用二型最大似然方法得到代价函数：

70、l({γi,bi},β)＝logc|+ytc-1y(26)，

71、其中，c＝β-1i+φtγφ，对代价函数的期望求偏导，再令其等于0，即可得到最大似然算法下的超参数的学习规则

72、

73、为了发掘块内信号的相关性，bsbl算法对信号xi的协方差矩阵bi加入约束

74、

75、利用bi的更新式可得到相关系数r的经验计算公式：

76、其中，为bi中次对角线的均值，为主对角线的均值，式(27)中超参数γi的计算复杂度较高，采用边界优化算法对式(26)进行优化，进一步对γi求偏导，再令其为0即可得到γi的学习规则：

77、由式(24)-式(32)即可得到doa估计值及块信号的重构值。

78、本发明步骤3中，极化参数的估计具体包括以下内容：将矢量化后的块信号恢复成矢量化前的信号，由4l×1的块信号按照相应的规则转换为2×2l的块信号；

79、根据酉矩阵的性质uuh＝i，有：

80、

81、取该矩阵的前l行，即：

82、

83、则可由此得出

84、由式(33)-式(36)即可实现极化参数的估计。

85、本发明与现有技术相比，能够显著提高参数估计性能。