纤维增强复合材料管道弯曲临界曲率半径预测方法与流程

本发明属于复合材料管道设计领域，具体涉及一种基于三维弹性力学理论的纤维增强复合材料管道弯曲临界曲率半径的预测方法。

背景技术：

1、随着石油天然气等能源需求的不断增长，对输送管道的性能要求也越来越高。传统的金属管道存在着重量大、耐腐蚀性差等缺点，已不能完全满足日益苛刻的工况条件。与金属管道相比，纤维增强复合材料管道具有比强度高、比模量高、耐腐蚀性好等优点，在海洋工程、化工、航空航天等领域得到了广泛应用。

2、已有的复合材料管道力学分析方法或由于基本假设的局限性而不能精确预测厚壁管道的力学行为，或由于计算成本高昂而难以应用于实际工程设计。因此，有必要发展一种适用于厚壁复合材料管道，同时计算效率又较高的力学建模与分析方法。本发明针对上述问题，提出了一种基于广义平面应变假设，考虑扩展剪切耦合效应，能够高效预测任意铺层角度厚壁复合材料管道弯曲变形行为的三维弹性力学解析方法。

技术实现思路

1、本发明的目的在于提供一种适用于厚壁纤维增强复合材料管道的三维弹性力学解析建模方法，该方法能够准确考虑扩展剪切耦合效应，高效预测任意铺层角度管道在弯曲载荷作用下的应力应变响应，并在此基础上给出管道临界弯曲半径的快速计算方法，为所述复合材料管道的抗弯曲性能设计提供理论依据。

2、为了实现上述目的，本发明采用的技术方案如下：

3、纤维增强复合材料管道弯曲临界曲率半径预测方法，其特征在于，包括以下步骤：

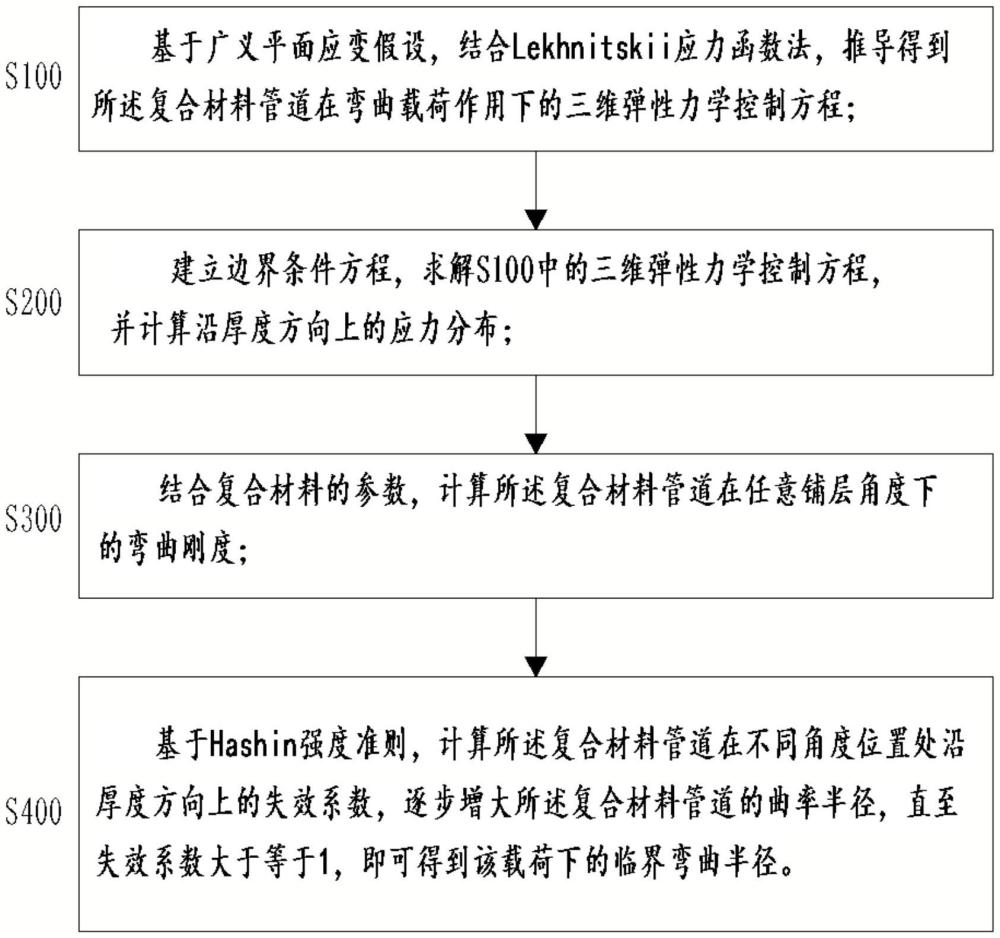
4、s100、基于广义平面应变假设，结合lekhnitskii应力函数法，推导得到所述复合材料管道在弯曲载荷作用下的三维弹性力学控制方程；

5、s200、建立边界条件方程，求解s100中的三维弹性力学控制方程，并计算沿厚度方向上的应力分布；

6、s300、结合复合材料的参数，计算所述复合材料管道在任意铺层角度下的弯曲刚度；

7、s400、基于hashin强度准则，计算所述复合材料管道在不同角度位置处沿厚度方向上的失效系数，逐步增大所述复合材料管道的曲率半径，直至失效系数大于等于1，即可得到该载荷下的临界弯曲半径。

8、进一步地，s100中的所述复合材料管道在弯曲载荷作用下的三维弹性力学控制方程组包括平衡方程和应变协调方程；

9、其中所述复合材料管道在弹性力学范畴内满足应变协调方程；

10、平衡方程引入lekhnitskii应力函数f和ψ并转化为关于f和ψ的高阶偏微分方程，平衡方程推导过程为：

11、s101、基于广义平面应变假设，确定应变分量；

12、s102、将广义hooke定律应用到复合材料的应力-应变方程中，得到复合材料的本构方程在材料主轴方向的表达式，复合材料的本构方程在材料主轴方向的表达式通过转换矩阵获得材料的柔度矩阵；

13、s103、引入lekhnitskii应力函数f(r，θ)和ψ(r，θ)，计算应力分量，得到平衡方程对应的偏微分方程，具体为：

14、

15、式中lij和算子的具体形式由复合材料的刚度系数决定。

16、进一步地，s101中基于广义平面应变假设，设置应变分量在柱坐标中的具体公式为：

17、

18、其中，u、v、w分别为径向、周向和轴向位移分量，εr，εθ，εz和γrθ，γθz，γrz为径向应变、周向应变、轴向应变和在r-θ平面内的剪切应变、θ-z平面内的剪切应变、r-z平面内的剪切应变。

19、进一步地，s102中将广义hooke定律应用到复合材料应力应变方程中，具体公式为：

20、σr＝c11εr+c12εθ+c13εz+c14γrθ

21、σθ＝c12εr+c22εθ+c23εz+c24γrθ

22、σz＝c13εr+c23εθ+c33εz+c34γrθ

23、trθ＝c14εr+c24εθ+c34εz+c44γrθ

24、τθz＝c55γθz+c56yrz

25、τrz＝c56yθz+c66γrz

26、其中σr，σθ，σz和τ为径向应力、环向应力、轴向应力和剪切应力。

27、进一步地，s103引入lekhnitskii应力函数f(r，θ)和ψ(r，θ)，计算应力分量的公式为：

28、

29、将lekhnitskii应力函数代入平衡方程和协调方程，并考虑轴向应变随r和θ线性变化的特点，得到关于f和ψ的偏微分方程组，即可得到平衡方程对应的偏微分方程。

30、进一步地，s200、建立边界条件方程，求解s100中的三维弹性力学控制方程的方法为：

31、联立三维弹性力学控制方程组中的平衡方程和应变协调方程两个方程组，即可求解得到lekhnitskii应力函数的具体表达式；

32、将应力函数f表示为关于r的幂级数形式，代入上式并利用柱坐标系下的调和条件，确定幂指数满足的特征方程，进而得到f的通解形式如下：

33、

34、将应力函数ψ表示为关于r的幂级数形式，得出关于ψ的非齐次偏微分方程：

35、

36、式中为另一组算子，其具体形式也由复合材料刚度系数确定p*(r)为关于r的函数，通过边界条件和本构方程求解；

37、求解上述非齐次偏微分方程，得到ψ的通解如下：

38、

39、其中，

40、

41、

42、λ1＝-2β14-6β24+β56，λ2＝4β44-β55，

43、λ3＝-β11-2β12+3β22-β66，λ4＝2β14-2β24+β56

44、其中，βij由材料的具体参数决定；

45、综上，结合应变-位移方程、lekhnitskii应力函数通解和本构方程，所述复合材料管道在弯曲载荷下的广义位移解表示为：

46、

47、其中，uk(r)、vk(r)和w(r)均为关于r的函数；其他参数：ξ是保证结构满足兼容性方程的常数值即周向协调因子，其他未知参数通过力学边界条件和连续条件建立关于未知系数的线性方程组，求解该方程组即可确定位移和应力分量的解析表达式。

48、进一步地，s300中计算所述复合材料管道在任意铺层角度下的弯曲刚度，所述复合材料管道管道的抗弯刚度ei表示为：

49、

50、利用数值积分方法，计算所述复合材料管道全局抗弯刚度。

51、与现有技术相比，本发明具有以下有益效果：

52、(1)充分考虑了厚壁复合材料管道中的扩展剪切耦合效应，建立了适用于任意铺层角度的三维弹性本构关系，较经典层合板理论具有更广的适用范围。

53、(2)与已有解析方法相比，本发明在理论上更加严格，不仅满足平衡方程，还满足应变协调方程。通过引入周向位移协调因子，解决了经典理论中周向位移不连续的问题。

54、(3)基于广义平面应变假设，在运动方程中引入了lekhnitskii应力函数，建立了平面问题到空间问题的解析过渡方法，避免了求解三维问题的困难。

55、(4)应力分量表示为幂级数形式，通过平衡方程与应变协调方程建立了幂指数与复合材料广义刚度系数之间的解析关系，并结合力学边界条件和连续条件确定了幂级数系数，获得了严格的三维弹性解。

56、(5)提出了基于弯曲刚度和强度的临界弯曲半径预测方法，实现了复合材料管道抗弯曲性能的快速评估，可用于指导工程设计。相比有限元分析，该方法计算成本大大降低。

57、(6)通过与有限元结果的对比，验证了本发明解析解的准确性。应用算例表明，所提出的临界弯曲半径预测方法能够准确揭示缠绕角度对管道抗弯曲性能的影响规律。